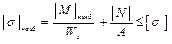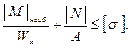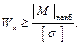Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия бруса при простых деформацияхСтр 1 из 11Следующая ⇒
ISBN
Рассмотрены разделы курса сопротивление материалов, относящиеся к расчётам на прочность и жёсткость при сложных деформациях, неравномерном движении ударном нагружении, переменных напряжениях и колебаниях упругих систем, а также энергетических методов определения перемещений и общих методов решения статически неопределимых систем. Предназначено для студентов очной, очно-заочной и заочной форм обучения, изучающих дисциплину «Сопротивление материалов»: Институт ракетно-космической техники: – по специальности 24.05.01 Проектирование, производство и эксплуатация ракет и ракетно-космических комплексов. – направлениям подготовки: 15.03.01 Машиностроение, 15.03.03 Прикладная механика, 22.03.02 Металлургия, 23.03.01 Технология транспортных процессов. 24.05.01 Ракетные комплексы и космонавтика. Институт двигателей и энергетических установок: –по специальности 15.03.05 Конструкторско-технологическое обеспечение машиностроительных производств; 24.03.05 Двигатели летательных аппаратов; 24.05.02 Проектирование авиационных и ракетных двигателей и направлению подготовки; – направлениям подготовки 13.03.03.Энергетическое машиностроение. изучающих дисциплину «Механика материалов и конструкций» по направлению подготовки: 13.03.03 Энергетическое машиностроение. Институт авиационной техники: – по специальности 24.05.07 Самолёто- и вертолётостроение; – направлениям подготовки: 15.03.05 Конструкторско-технологическое обеспечение машиностроительных производств; 24.03.04, Авиастроение, 25.04.01 Техническая эксплуатация летательных аппаратов и двигателей. 27.03.02 Управление качеством. Подготовлено на кафедре сопротивления материалов Самарского университета.
ISBN УДК 539.3/6(075) ББК 30.121я7
ОГЛАВЛЕНИЕ 1. Потенциальная энергия деформации и общий метод 1.1. Потенциальная энергия бруса при 1.1.1. Центральное растяжение и сжатие (ЦРС)…….....…..7 1.1.2. Плоский изгиб……………………………………..…..9 1.1.3. Кручение…………………………………………..….10
1.2. Обобщённая сила и обобщённое перемещение. 1.4. Взаимность работ и взаимность перемещений…….........12 1.5. Интеграл Мора для определения перемещений 1.6. Графоаналитический способ вычисления 1.8. Правила перемножения эпюр при использовании 1.9. Формулы для площадей и положения центров 1.10. Вопросы для самопроверки…………………………..…...23 2. Наиболее общие методы раскрытия 2.1 Метод сил………………………………………………..…….24 2.2 Уравнение трёх моментов……………………………..……...29 2.3 Вопросы для самопроверки…………………………………..34 3 Сложное сопротивление бруса……………………………….35 3.1 Общий случай сложного сопротивления бруса…………...35 3.1.1 Напряжения и расчёт на прочность в 3.1.2 Перемещения бруса в общем случае 3.2 Расчёт плоских статически неопределимых рам 3.2.1 Пример расчёта плоской 3.3 Косой изгиб……………………………………………..….48 3.3.1 Напряжения и расчёт на прочность 3.3.2 Перемещения при косом изгибе…………...……….…54 3.4 Внецентренное растяжение и сжатие 3.5 Кручение с изгибом………………………………..….......59 3.6 Вопросы для самопроверки……………………….………63 4 Прочность при циклически изменяющихся 4.1 Основные понятия об усталостном разрушении...........…64 4.2 Предел выносливости материала 4.3 Предел выносливости материала 4.4 Концентрация напряжений и её влияние 4.5 Предел выносливости детали
4.6 Предел выносливости детали 4.7 Расчёт на прочность при переменных напряжениях 4.8 Расчёт на прочность при переменных напряже- 4.9 Практические способы борьбы 4.10 Вопросы для самопроверки……………………..….……94 5 Колебания упругих систем………………………………….96 5.1 Основные понятия об упругих колебаниях…....…..…….96 5.2 Собственные колебания системы с одной степенью свободы..………………………….…..97 5.3 Собственные колебания системы с одной степенью 5.4 Вынужденные колебания системы с одной степенью 5.5 Расчёт системы с одной степенью свободы 5.6. Собственные колебания системы 5.7. Вопросы для самопроверки……………………....………112 6. Ударное нагружение..……………………………………….113 6. 1. Перемещения, напряжения и расчёт на 6. 2. Частные случаи и особенности сопротивления 6.2.1. Мгновенное нагружение.………………………..…….117 6.2.2. Изгибающий удар.…………………………..…..……..117 6.2.3. Особенности сопротивления удару 6.2.4. Правило выравнивания поперечного сечения 6.3 Вопросы для самопроверки..………………….…….…….121 7 Расчёт на прочность неравномерно движущихся 7.1. Напряжения и расчёт на прочность неравно 7.2. Вопросы для самопроверки.………………………............125 8. Расчёт толстостенных цилиндров.………………………...126 8.1. Напряжения в толстостенном цилиндре, 8.2. Расчёт толстостенного цилиндра, 8.2.1. Расчёт по допускаемым напряжениям……………...131 8.2.2. Расчёт по предельным нагрузкам………….………...132 8.3 Применение составных цилиндров 8.4 Вопросы для самопроверки………………………..….......138 9. Тонкостенные оболочки.……………………………............139 9.1. Напряжения в осесимметричной оболочке 9.2. Расчёт на прочность сферической оболочки.…….....…...141 9.3. Расчёт на прочность цилиндрической оболочки..…..….142 9.4. Расчёт на прочность конической оболочки, 9.5 Вопросы для самопроверки………………………..….…..145 10 Продольно-поперечный изгиб.…………………………...146 10.1 Точное решение уравнения 10.2 Приближённое решение уравнения 10.3 Расчёт на прочность при продольно- 10.4 Вопросы для самопроверки………………………….….154 11. Сопротивление материалов и другие науки
11.1 Сопротивление материалов……………………….……155 11.2 Теория упругости…………………………………..……155 11.3 Теории пластичности и ползучести……………………159 11.4 Строительная механика…………………………………160 11.5 Материаловедение………………………………………160 11.6 Вопросы для самопроверки……………………….….…160 Список литературы...………………………………..………….161 1. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Плоский изгиб
После нагружения балка искривляется по дуге окружности, а опорные сечения поворачиваются на угол θ. Продолжим направления опорных сечений до пересечения в центре окружности К. Выразим θ через М
где М – изгибающий момент, E · J – жёсткость балки при изгибе. Этот результат также можно было получить и интегрированием дифференциального уравнения изогнутой оси балки. Запишем формулу для работы пар сил при статическом (медленном) нагружении.
Теперь запишем формулу для энергии
Рассмотрим поперечный изгиб. Это, более сложный случай. Изобразим балку, испытывающую поперечный изгиб (рис. 1.4, а). Выделим бесконечно малый элемент длиной d z. Покажем его отдельно (рис. 1.4, б). Пусть Q > 0 и M > 0. Чтобы вычислить энергию, накопленную элементом, нужно вычислить работу внешних сил (для элемента – это Q и M). Оказывается, что Aq << Am, поэтому силами Q можно пренебречь и мы получим для элемента, случай чистого изгиба (рис. 1.4, в), тогда
Интегрируя по длине всей балки, получим общую формулу для энергии деформации балки при поперечном изгибе
Кручение
На свободном конце брус нагружен парой сил M 0. Свободный конец бруса поворачивается на угол φ. Очевидно, что М к = М 0 = const. Аналогично предыдущим простым деформациям запишем
Далее рассмотрим общий случай (М к ≠ const) и по аналогии с предыдущими случаями получим общую формулу для энергии деформации бруса при кручении
Полученные формулы чрезвычайно важны. Они используются при выводе универсального уравнения для определения перемещений.
Пример 2. Рассмотрим консольную балку, нагруженную распределённой нагрузкой Можно ли к этому треугольнику применить наши формулы и чему равен? Составляем уравнение для изгибающих моментов.
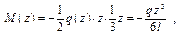 видно, что это одночленная степенная функция. Следовательно, наши формулы применять можно, видно, что это одночленная степенная функция. Следовательно, наши формулы применять можно,причём n = 3. В реальных конструкциях интенсивность может быть распределена по более сложному закону, но её можно привести к простым. Пример 3. Рассмотрим консольную балку, нагруженную распределённой нагрузкой Чтобы применить формулу Верещагина, необходимо поступить следующим образом: 1 способ – определить реакции в опоре а и расслоить эпюры по левым силам; 2 способ – дополнить распределённую нагрузку до полной и вычесть дополненную. Расслаивать эпюры, по правым силам. Вопросы для самопроверки 1. Как записывается потенциальная энергия деформации бруса при центральном растяжении или сжатии? 2. Как записывается потенциальная энергия бруса при изгибе? 3. Как записывается потенциальная энергия бруса при кручении? 4. Что понимается под обобщённой силой? 5. Что представляет собой обобщённое перемещение? 6. Что называется податливостью? Как она определяется? 7. Как записывается интеграл Мора для определения перемещений при изгибе? 8. Каков порядок определения прогибов с помощью интеграла Мора? 9. Каков порядок определения углов поворота с помощью интеграла Мора? 10. Как записывается формула Верещагина для определения перемещений при изгибе? 11. Какие ограничения накладываются при применении способа Верещагина? 12. Каков порядок определения прогибов с помощью способа Верещагина? 12. Каков порядок определения углов поворота с помощью способа Верещагина? 13. Как производится перемножение эпюр при использовании способа Верещагина, если единичная эпюра – ломаная прямая? 13. Каким свойством можно воспользоваться при определении перемещений способом Верещагина, если и единичная и грузовая эпюра – линейные функции. 14. Как производится перемножение эпюр при использовании способа Верещагина, если грузовая эпюра – сложная фигура? 15. В чём заключается расслоение грузовых эпюр при использовании способа Верещагина? 16. Как можно проводить расслоение грузовых эпюр при использовании способа Верещагина? 2. НАИБОЛЕЕ ОБЩИЕ МЕТОДЫ РАСКРЫТИЯ Метод сил Метод сил – один из общих универсальных методов раскрытия статической неопределимости. Есть ещё метод деформаций, но он применяется при расчёте сооружений. В машиностроении при расчёте машин чаще всего применяется метод сил. Метод сил позволяет составить уравнения совместности деформаций или уравнения перемещений. Он даёт стандартный подход вне зависимости от вида конструкции.
Приступим к выводу уравнений метода сил. Рассмотрим частный случай, но уравнения получим общие. Будем рассматривать неразрезную балку (рис. 2.1, а). Неразрезной называют такую балку, которая, не прерываясь, перекрывает несколько пролётов. Эти несколько пролётов можно перекрыть и разрезными балками. Неразрезная балка имеет преимущества: у неё больше жёсткость, то есть меньше перемещения и, в большинстве случаев, больше грузоподъёмность. Недостаток – неразрезная балка – статически неопределимая балка и в ней могут быть монтажные напряжения, связанные с неточной установкой опор. Несмотря на этот недостаток, неразрезные балки широко применяются в конструкциях летательных аппаратов. В сооружениях применяются разрезные балки. Опоры нумеруются 0, 1, 2, 3, 4 (слева направо). На балку действуют активные силы и реакции опор. Неизвестных реакций шесть, а статика даёт три уравнения. Таким образом имеем три лишних неизвестных (лишних – с точки зрения статики), то есть балка три раза статически неопределима. У балки три промежуточных опоры и всегда, стёпень статической неопределимости равна числу промежуточных опор. Для решения задачи необходимо назначить лишние неизвестные. За лишние можно принять любые неизвестные, но после отбрасывания лишних неизвестных, система должна быть геометрически неизменяемой даже в малом. Примем за лишние неизвестные реакции промежуточных опор Х 1 = R 1, Х 2 = R 2, Х 3 = R 3. После назначения лишних неизвестных, изображаем основную систему (рис. 2.1, б). Основной системой (ОС) называют статически определимую и геометрически неизменяемую систему, которая получается из исходной статически неопределимой, после отбрасывания лишних связей и внешних сил. Лишние связи – связи, в которых возникают лишние неизвестные, то есть в нашем случае, лишними связями будут промежуточные опоры. Видно, что основная система – геометрически неизменяемая и статически определимая. Далее изображаем эквивалентную систему (рис. 2.1, в). Эквивалентная система (ЭС) – это основная система, нагруженная активными силами и лишними неизвестными. Реакцию 0 не показываем, так как из уравнений статики, R 0 = 0. Почему эта система называется эквивалентной? Эквивалентная система в точности воспроизводит исходную статически неопределимую систему с точки зрения сил, перемещений, деформаций и напряжений. Далее, все вопросы, будем решать с эквивалентной системой. Метод сил позволяет составить уравнение совместности деформаций. В чём заключаются закономерности деформаций изучаемой системы? Она заключается в том, что в эквивалентной системе, перемещения в направлении "лишних" связей, должны быть равны нулю. Или иначе: Х 1, Х 2, Х 3 должны быть такими, чтобы в сечениях 1, 2, 3 эквивалентной системы прогибы обращались в ноль, то есть ∆1 = 0, ∆2 = 0, ∆3 = 0. Распишем первое соотношение. Для этого рассмотрим ряд нагружений основной системы и перемещения от этих нагружений. Первое нагружение. Приложим к основной системе единичную силу (рис. 2.2, а), соответствующую первой неизвестной силе Х 1. Прогиб равен δ 11.
Следующее нагружение основной системы силой Х 1 (рис. 2.2, б). Тогда ∆11 = δ 11· Х 1. Далее изобразим основную систему и нагрузим единичной силой, соответствующей второй неизвестной силе Х 2 (рис. 2.2, в). Затем нагрузим основную систему силой Х 2 (рис. 2.2, г) и получим перемещение ∆12 = δ 12· Х 2. Теперь нагрузим основную систему в сечении 3 вначале единичной силой (рис. 2.2, д), а затем силой Х 3 (рис. 2.2, е) и получим перемещение ∆13 = δ 13· Х 3. Мы рассмотрели нагружения неизвестными силами. Остаётся рассмотреть нагружение активными силами (рис. 2.2, ж) и получить перемещение ∆1 F. Используя принцип суперпозиции, мы получаем первое из уравнений совместности деформаций. Аналогично получаем ещё два уравнения. Первый индекс у ∆ (δ) будет совпадать с номером уравнения
Мы получили основные уравнения метода сил или канонические уравнения метода сил, для три раза статически неопределимой системы. Это, по существу, уравнения совместности деформаций. Физический смысл канонических уравнений – перемещения в эквивалентной системе, по направлению лишних неизвестных равны нулю. Запишем эти уравнения в общем виде для п -раз статически неопределимой системы.
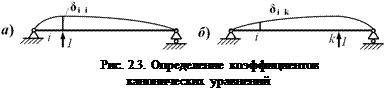
Здесь δ ik – коэффициенты канонических уравнений – это перемещения в основной системе по направлению i -й лишней связи от единичного силового фактора, соответствующего лишнему неизвестному Xk. При i = k получаем главные коэффициенты или главные податливости основной системы (податливость – перемещение от единичной силы). Если i ≠ k, то это побочные коэффициенты канонических уравнений (побочные податливости). Вспомним о взаимности перемещений (δ ik = δ ki). Иначе говоря, матрица коэффициентов канонических уравнений симметрична относительно главной диагонали. Таким образом, нужно определять не все коэффициенты канонических уравнений, а только главные коэффициенты и коэффициенты, расположенные по одну стороны от главной диагонали. Поэтому вычисление коэффициентов канонических уравнений несколько упрощается. ∆ iF – свободные члены канонических уравнений – перемещения в основной системе по направлению i -й лишней связи от всех внешних сил. Канонические уравнения метода сил применимы к любому твёрдому телу, конструкции, которую можно считать линейной, то есть подчиняющейся закону Гука. Лишними неизвестными могут быть силы, пары сил и обобщённые силы. Мы будем применять их главным образом к стержневым системам, испытывающим изгиб. В этом случае можно получить несложные уравнения для подсчёта коэффициентов (рис. 2.3, а-б).
Вспомним интеграл Мора: 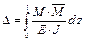 . .
Получим формулу для δ ik. Здесь
– общая формула для определения коэффициентов канонических уравнений. Аналогично получим формулу для ∆ iF. Здесь M = MF – изгибающий момент от всех внешних сил,
– формула для определения свободных членов канонических уравнений. Все моменты, в полученных формулах, вычисляются при соответствующем нагружении в основной системе. Для прямолинейных стержней коэффициенты и свободные члены канонических уравнений, можно вычислять способу Верещагина. Пример. Построить эпюры внутренних сил для заданной балки (рис. 2.4). 1) Определяем степень статической неопределимости системы: неизвестных реакций – 4, уравнений статики – 3. Система один раз статически неопределима. 2) Выбираем основную систему – за лишнюю связь принимаем реакцию шарнирной опоры. 3) Строим эквивалентную систему 4) Записываем каноническое уравнение метода сил для эквивалентной системы
5) Определяем коэффициент и свободный член канонического уравнения. Для этого последовательно нагружаем основную систему единичной силой, соответствующей Х 1, и активной силой М, строим эпюры
6) Подставляем полученные значения в каноническое уравнение и раскрываем статическую неопределимость.
7) Строим эпюры поперечных сил и изгибающих моментов в эквивалентной системе. Уравнение трёх моментов Рассмотрим неразрезную многопролётную балку (рис. 2.5, а). За лишние неизвестных при выборе основной системы удобнее принять изгибающие моменты в опорных сечениях. В этом случае основная система будет системой однопролётных балок, соединённых на опорах шарнирами. Изобразим основную систему (рис. 2.5, б), а затем эквивалентную систему (рис. 2.5, в) – она будет представлять ряд простых шарнирно-опёртых балок, нагруженных активными силами и неизвестными изгибающими моментами по концам. Рассмотрим m -ое уравнение системы канонических уравнений метода сил:
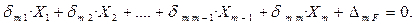
Определим коэффициенты этого уравнения по формуле
В связи с тем, что основная система представляет собой систему однопролётных балок, то в m -ом уравнении отличны от нуля будут только коэффициенты δ m m –1, δ m m,, δ m m +1. Все остальные коэффициенты обратятся в ноль, так как единичный опорный момент создаёт изгибающие моменты только в соседних пролётах АВ и ВС. Нагружаем основную систему единичными парами сил поочерёдно в сечениях m – 1, m, m + 1 (рис. 2.5, г-е) и вычисляем коэффициенты
Далее нагружаем основную систему активными силами (рис. 2.5, ж) и определяем ∆ mF по формуле
где Ω m, Ω m + 1 – площади эпюр изгибающих моментов от активных сил, приложенных к основной системе на m -ом и (m + 1)-ом пролётах, Sm, Ω m + 1 – статические моменты площадей эпюр изгибающих моментов от активных сил, приложенных к основной системе на m -ом и (m + 1)-ом пролётах. Подставим полученные значения коэффициентов в каноническое уравнение метода сил
Видно, что в полученное уравнение входят размеры и силовые факторы, относящиеся только к двум соседним пролётам АВ и ВС. Это уравнение, выражающее тот факт, что взаимный угол поворота смежных сечений пролётов АВ и ВС на m -ой опоре должен быть равен нулю. По отношению к опоре (которую будем называть средней) опора m – 1 будет левой, а опора m + 1 будет правой, соответственно и пролёты – левый и правый. Поэтому введём новые обозначения Mm –1 = M л, Mm = M ср, Mm +1 = M п, тогда
– уравнение трёх моментов. При использовании уравнения трёх моментов последовательно рассматриваются все пары соседних пролётов, причём число пар пролётов, следовательно, и уравнений, равно числу промежуточных опор, то есть степени статической неопределимости неразрезной балки. Если неразрезная балка имеет защемление или консоль (рис. 2.6, а), то в этих случаях поступают следующим образом:
При построении эпюр поперечных сил и изгибающих моментов силу F снова устанавливают в конце консоли. Теперь, о консоли. При раскрытии статической неопределимости силу F переносят на опору 3 (рис. 2.6, в), в результате получается на опоре действует пара сил М 0 = F · l 4. Сила, приложенная к опоре, имеет значение только при определении реакций опор, изгибающих моментов она не создаёт. Затем, при составлении уравнений трёх моментов для опоры 2, пару сил считают опорным моментом и тогда М п = F · l 4. При построении эпюр поперечных сил и изгибающих моментов силу F снова устанавливают в конце консоли. Пример. Построить эпюры внутренних сил для заданной балки (рис. 2.7, а). 1) Определяем степень статической неопределимости системы: неизвестных – 4, уравнений статики – 3. Система один раз статически неопределима. 2) Выбираем основную систему – заменяем заделку фиктивным пролётом l 1 = 0 (рис. 2.7, б). 3) Строим эквивалентную систему (рис. 2.7, в). 4) Записываем уравнение трёх моментов для эквивалентной системы
5) Нагружаем основную систему активной силой, строим расслоённую эпюру М F вычисляем известные величины уравнения трёх моментов (рис. 2.7, г, д). 6) В нашем случае l 1 = 0, l 2 = l, М 0 = 0, S л = 0,
7) Подставляем полученные величины в уравнение трёх моментов и раскрываем статическую неопределимость
8) Строим эпюры поперечных сил и изгибающих моментов Вопросы для самопроверки 1. Как производится расчёт статистически неопределяемых конструкций с помощью метода сил (последовательность расчёта)? СЛОЖНОЕ СОПРОТИВЛЕНИЕ БРУСА Генеральная проверка.
Для генеральной проверки выбирается новая основная система (НОС) (рис. 3.14, а). Для этого необходимо взять все новые лишние связи. В нашем случае, за новые лишние связи примем связи на левой опоре. Показываем новую эквивалентную систему (НЭС) и перемещения в направлении новых неизвестных (рис. 3.14, б). Эти перемещения в эквивалентной системе должны быть равны нулю.
Однако из-за погрешностей вычислений в большинстве случаев добиться нулевого результата не удаётся. Поэтому более удобно разделить силы на активные и реактивные (реакции отброшенных связей), определить перемещения в основной системе отдельно от активных сил ∆i А (рис. 3.14, в) и отдельно от реактивных сил ∆ iR
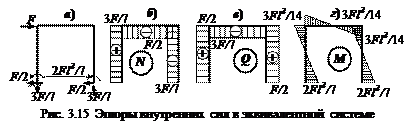
Если такие соотношения выполняются по всем новым перемещениям, то статическая неопределимость раскрыта верно. Теперь строим в эквивалентной системе (рис. 3.15, a) эпюры внутренних силовых факторов (N, Q, M) (рис. 3.15, б-в) и проводим расчёт на прочность.
– условие прочности для любого сечения. Поскольку
– условие прочности для всей рамы.
Расчёт на прочность
Это условие прочности для всей рамы и так решается первая задача сопротивления материалов. Здесь N – нормальная сила в сечении, где действует | М| наиб. Вторая задача – подбор размеров поперечного сечения – приводится из условия прочности при изгибе
Затем подобранное сечение проверяется по полному условию прочности. Третья задача – определение грузоподъёмности – эта задача решается только в каждом конкретном случае. Косой изгиб 3.3.1. Напряжения и расчёт на прочность Вспомним плоский изгиб. Брус (рис. 3.17, а) испытывает плоский изгиб, так как прогибы лежат в плоскости изгибающих сил (в плоскости полного изгибающего момента). Теперь, о косом изгибе (рис. 3.17, б). Брус испытывает косой изгиб, если он нагружен силами, перпендикулярными его оси и парами сил, плоскость действия которых не совпадает ни с одной из главных плоскостей жёсткости бруса.
Изобразим поперечное сечение бруса, покажем его главные центральные оси и плоскость полного изгибающего момента. При таком изгибе, плоскость перемещений не совпадает с плоскостью полного изгибающего момента. Приступим к выводу формулы для напряжений. Будем рассматривать частный случай, но формулу получим для общего случая. Рассмотрим консольную балку, нагруженную силой и произвольное сечение этой балки. С – центр тяжести поперечного сечения
Представим косой изгиб как сумму простых деформаций. Для этого разложим силу на составляющие Fx и Fy: Fx = F ·sin φ, Fy = F ·cos φ. Каждая составляющая вызывает плоский поперечный изгиб: Fx – в плоскости наименьшей жёсткости, a Fy – в плоскости наибольшей жёсткости бруса. Применим принцип суперпозиции
Далее подставляем в исходную формулу значения компонент и получаем
Здесь F · z · = M – полный изгибающий момент, тогда
Это почти окончательная формула. Почему? Знак изгибающего момента может быть и положительным, поэтому в формуле нужно поставить два знака
Здесь M – полный изгибающий момент в рассматриваемом сечении, берётся по абсолютной величине, а знак перед M должен совпадать со знаком напряжений в первой четверти; х, у – координаты точки, в которой определятся напряжение
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.15.94 (0.162 с.) |
 Рассмотрим чистый изгиб
Рассмотрим чистый изгиб 

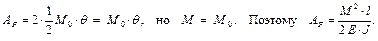
 – формула для энергии деформации балки при чистом изгибе.
– формула для энергии деформации балки при чистом изгибе.
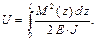
 Рассмотрим брус круглого поперечного сечения, подверженный кручению. Пусть брус одним концом защемлён (рис. 1.5) (но это не обязательно).
Рассмотрим брус круглого поперечного сечения, подверженный кручению. Пусть брус одним концом защемлён (рис. 1.5) (но это не обязательно).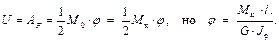
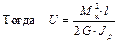 – формула для энергии деформации при кручении в случае М к = const.
– формула для энергии деформации при кручении в случае М к = const.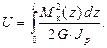
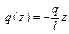 (рис. 1.19, б). Построим эпюру изгибающих моментов.
(рис. 1.19, б). Построим эпюру изгибающих моментов.
 (рис. 1.19, в). Без промежуточных вычислений запишем уравнение для изгибающих моментов.
(рис. 1.19, в). Без промежуточных вычислений запишем уравнение для изгибающих моментов. можно видеть, что к этому треугольнику формулы не применимы.
можно видеть, что к этому треугольнику формулы не применимы.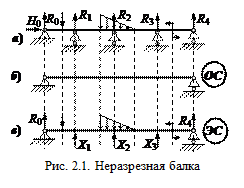

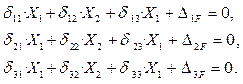
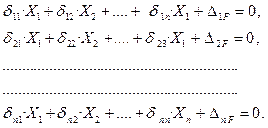
 – изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xk,
– изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xk,  – изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xi, тогда
– изгибающий момент от единичного силового фактора, соответствующего лишней неизвестной Xi, тогда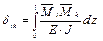 .
.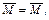 . Подставив в интеграл Мора. получим.
. Подставив в интеграл Мора. получим.
 δ 11· Х 1 + ∆1 F = 0.
δ 11· Х 1 + ∆1 F = 0.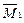 и MF. Используем способ Верещагина
и MF. Используем способ Верещагина
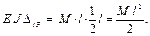
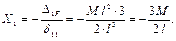

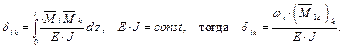

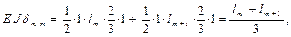
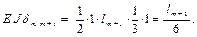
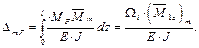
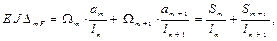
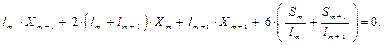
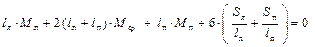
 Вместо заделки вводят две бесконечно близкие шарнирные опоры (рис. 2.6, б) (0 и 1), далее составляют уравнение трёх моментов, принимая М 0 = 0 и l 0 = 0. Теперь, о консоли. При раскрытии статической неопределимости силу F переносят на опору 3 (рис. 2.6, в), в результате получается на опоре действует пара сил М 0 = F · l 4. Сила, приложенная к опоре, имеет значение только при определении реакций опрор, изгибающих моментов она не создаёт. Затем, при составлении уравнений трёх моментов для опоры 2, пару сил считают опорным моментом и тогда М п = F · l 4.
Вместо заделки вводят две бесконечно близкие шарнирные опоры (рис. 2.6, б) (0 и 1), далее составляют уравнение трёх моментов, принимая М 0 = 0 и l 0 = 0. Теперь, о консоли. При раскрытии статической неопределимости силу F переносят на опору 3 (рис. 2.6, в), в результате получается на опоре действует пара сил М 0 = F · l 4. Сила, приложенная к опоре, имеет значение только при определении реакций опрор, изгибающих моментов она не создаёт. Затем, при составлении уравнений трёх моментов для опоры 2, пару сил считают опорным моментом и тогда М п = F · l 4.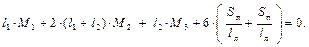


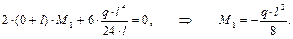

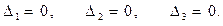


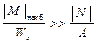 (рис. 3.16), то наиболее опасным будет сечение, где действует | М| наиб.
(рис. 3.16), то наиболее опасным будет сечение, где действует | М| наиб.