
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт на прочность при переменных напряжениях в случае линейного напряжённого состояния и чистого сдвига
Почему ограничиваемся этими двумя напряжёнными состояниями? Так как, все предыдущие выводы, касались этих случаев: линейное напряжённое состояние – растяжение-сжатие, изгиб (касательными напряжениями пренебрегаем), сдвиг, кручение. В расчётах на прочность при переменных напряжениях традиционно используют, не допускаемое напряжение, а коэффициент запаса. Вычисляется коэффициент запаса и сравнивается с необходимым значением. Поэтому предстоит вывести формулу для коэффициента запаса. Изобразим схематизированную диаграмму предельных амплитуд цикла для детали (рис. 4.18): Ниже прямой АЕ лежат неразрушающие циклы, выше – разрушающие.
Между прямыми СЕ и ВЕ разрушение не происходит, но напряжения выше предела текучести – деталь изменяет свою форму, размеры и нарушается нормальная работоспособность, поэтому мы должны ограничить работу детали по пределу текучести: pm ах = pm + p а ≤ p т. В пределе pm + p а = p т – это уравнение прямой, получим его в отрезках:
Видно, что прямая отсекает на координатных осях отрезки, равные пределу текучести материала, ОВ = р т. Точка пересечения прямых АЕ и ВС находится вблизи точки М 0, через которую проведена схематизация по усталости. Диаграмма АСВ – окончательная схематизированная диаграмма предельных амплитуд цикла напряжений для детали. Теперь приступим к выводу формулы для коэффициента запаса. Пусть в точке детали, для которой вычисляется коэффициент запаса, действуют напряжения, параметры которых рт, ра. Изобразим точку М (рт, ра). Спрашивается, с каким предельным циклом сравнивать данный цикл? Существует правило: заданный цикл сравнивается с подобным предельным циклом, так как во многих случаях, переход к предельному циклу при возрастании внешних сил происходит, как правило, при пропорциональном изменении параметров цикла. Правда, так бывает, не всегда. Изобразим точку М R, соответствующую предельному циклу, подобному заданному, с которой мы будем сравнивать заданный цикл Далее найдём коэффициент запаса, п R – коэффициент запаса по усталостному разрушению (есть ещё, по текучести).
Мы рассматриваем случай, когда среднее напряжение положительное, поэтому Из условия подобия треугольников ОМ R К и ОМ D –
– эта формула используется для графического определения коэффициента запаса по усталостному разрушению (по усталости). Выведем аналитическую зависимость. Через точку М проведём прямую PQ, параллельную прямой AE: PQ – линия равноопасных циклов. Точки на этой прямой соответствуют циклам с одинаковым коэффициентом запаса. Из подобия треугольников OMrE и OMQ
отрезок DQ найдём из подобия треугольников OAE и DMQ
– формула для коэффициента запаса по усталостному разрушению. Эта формула справедлива для положительного среднего напряжения цикла, то есть при рт > 0. Здесь
Возникает вопрос: как быть, если средние напряжения сжимающие (рт < 0)? Экспериментальных данных мало, они противоречивы. С.В. Серенсен предложил: при рт > 0, ψр нужно брать из таблиц, а при рт < 0 – ψр = 0. Если считать, что ψр = 0, отрезок ОЕ влево, будет бесконечно большим, то есть диаграмма предельных амплитуд цикла – прямая, параллельная оси рт. По Иванову С.И. ψр = 0 при небольших сжимающих средних напряжениях. Если напряжения большие, то предлагается поступить следующим образом:
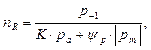
то есть диаграмма симметрична относительно начала координат. А как, фактически? Очевидно, по штриховой линии (рис. 4.19). Возвращаемся к рисунку 4.18. Мы рассмотрели точку Mr, когда она лежит выше точки С. Если прямая пересекает диаграмму ниже точки С, тогда нужно вычислять коэффициент запаса по текучести
Таким образом, если точка, соответствующая предельному циклу находится выше точки С, то коэффициент запаса вычисляется по усталостному разрушению, если ниже – по текучести. Но заранее неизвестно, где лежит точка С, поэтому вычисляются оба коэффициента запаса. А в каких точках и сечениях детали, вычисляется п? Коэффициент запаса вычисляется для самой опасной точки детали. Во-первых, там, где действуют наибольшие номинальные напряжения. Во-вторых, есть ещё, коэффициент К, поэтому, самой опасной, может оказаться точка, где есть концентрация напряжений. Поэтому, при расчёте деталей на прочность, коэффициенты запаса вычисляют: 1) в точках с наибольшими номинальными напряжениями;
2) в точках с концентрацией напряжений. Затем принимается наименьший из коэффициентов запаса – это и будет, коэффициент запаса детали. Точка с наименьшим коэффициентом запаса – самая опасная точка детали. Именно в ней произойдёт разрушение детали, при увеличении переменных напряжений. Для коэффициентов запаса есть нормы, которые для деталей авиационных двигателей выпускает ЦИАМ, а для деталей планера – ЦАГИ. В справочниках содержатся необходимые данные по коэффициентам запаса для различных видов деталей: п = 1,2 … 3,0. Коэффициенты запаса п установлены на основании горького опыта. Сломается деталь — коэффициент запаса повышается, не сломается – понижается. Например, для авиа трубопроводов, коэффициент запаса п = 3,0. 4.8. Расчёт на прочность при переменных напряжениях Как и при простом напряжённом состоянии, предстоит вывести формулы, для определения коэффициентов запаса по усталостному разрушению п r и по текучести п т. Экспериментальных данных при сложном напряжённом состоянии мало – это весьма сложные и дорогостоящие опыты, поэтому их проводилось мало. Обычно, для оценки прочности, используют статические теории прочности. Будем обобщать статические теории прочности, для переменных напряжений. Об опытах, которые проведены при сложном напряжённом состоянии.
1) Довольно подробные опыты проведены при кручении с изгибом. Напомним тип напряжённого состояния при кручении с изгибом (рис. 4.20, а). 2) Эти опыты проводились на лабораторных образцах, то есть изучалась усталость материала. 3) Испытания на усталость проводились при симметричном цикле изменения компонент и синфазном изменении нормальных и касательных напряжений. Покажем график изменения напряжений (рис. 4.20, б). Покажем результаты испытаний на усталость, в виде диаграммы σ – τ. Нам предстоит показать полученную, в результате испытаний на усталость, зависимость 1) при 2) при
Используя уравнение предельной кривой, получим формулу для коэффициента запаса. Здесь логично сравнивать эквивалентные напряжения, взятые, по той или иной теории прочности, например, по IV теории, так как материалы, используемые в авиа- и двигателестроении, как правило, пластичные
Возникает вопрос, с каким предельным циклом следует сравнивать заданный цикл? Возвращаемся к диаграмме предельных амплитуд циклов (см. рис. 4.18). Как и при простых деформациях, здесь принято считать, что движение к предельному циклу, происходит при пропорциональном изменении компонент напряжённого состояния. Если основываться на этом предположении (допущении), то нужно провести прямую из начала координат через точку М (σа, τа), найти предельную точку М R и подсчитать
Такую же операцию можно проделать и со знаменателем, тогда
Далее необходимо выразить
но
– окончательная формула для коэффициента запаса по усталостному разрушению при кручении с изгибом. Эта формула получена по результатам обработки экспериментальных данных с лабораторными образцами при симметричном цикле и синфазном изменении нормальных и касательных напряжений. Были проведены опыты (С.В. Серенсен) на деталях, чтобы выяснить, можно ли использовать полученную формулу в более сложных случаях. Оказалось, что можно, так как заметных ошибок не возникает. Поэтому, полученную формулу будем применять, и для деталей при несимметричных циклах и несинфазном изменении нормальных и касательных напряжений – опыты, это подтверждают. Парциальные коэффициенты запаса определяются по формулам
Далее нужно вычислить коэффициент запаса по текучести
А как получить
Меньшее из двух коэффициентов запаса п r и п т будет коэффициентом запаса в исследуемой точке. В деталях приходится искать коэффициенты запаса в нескольких опасных точках – самой опасной будет та точка, где коэффициент запаса, наименьший. 4.9. Практические способы борьбы Существуют конструктивные, технологические, эксплуатационные, металлургические и профилактические мероприятия по повышению несущей способности и долговечности деталей, работающих при переменных напряжениях. Остановимся на некоторых мероприятиях, наиболее часто используемых, на практике.
Конструктивные мероприятия сводятся, в основном, к уменьшению концентрации напряжений в местах нарушения призматической формы деталей (галтели, выточки, шпоночные пазы, шлицы, напрессованные на валы и оси втулки, отверстия и так далее). В галтельных переходах уменьшение концентрации напряжений достигается увеличением радиуса галтели. Если увеличение радиуса невозможно, то галтель выполняют с поднутрением (рис. 4.23) или рядом с галтельным переходом изготавливают разгружающую канавку (рис. 4.24).
 Уменьшение местных напряжений в шпоночных пазах достигается применением, при изготовлении паза, продольного фрезерования Уменьшение местных напряжений в шпоночных пазах достигается применением, при изготовлении паза, продольного фрезерования (рис. 4.25, а) в отличие, от торцевого (рис. 4.25, б). Использование эвольвентных шлицев по сравнению с прямоугольными приводит к существенному увеличению предела выносливости и долговечности вала. Прочность вала с напрессованной втулкой можно повысить увеличением диаметра в месте запрессовки (рис. 4.26, а). Для вала с отверстием – применением разгружающих пазов (рис. 4.26, б) или разгружающих буртов, то есть увеличением диаметра вала в месте расположения отверстия (рис. 4.26, в). Технологические мероприятия направлены на повышение качества поверхностного слоя деталей, особенно зон концентрации напряжений: тщательная обработка поверхности, защита поверхности различными покрытиями, создание благоприятного распределения остаточных напряжений. Наиболее простыми, дешёвыми и до
ступными методами повышения сопротивления усталости деталей являются методы поверхностного пластического деформирования (ППД). Чаще всего, при производстве деталей летательных аппаратов и двигателей применяются такие методы ППД, как гидро- и пневмо-дробеструйная обработка, обработка микрошариками, алмазное выглаживание, раскатка. Поверхностным пластическим деформированием упрочнялось 21% всех деталей планера самолёта ТУ-154, в том числе: 38% – деталей шасси, 25% – крыла и оперения, 15% – мотогондолы, 11% – фюзеляжа, 5% – гондолы шасси. При изготовлении деталей авиационных двигателей упрочнение ППД использовалось более широко. Так на двигателе " Е " конструкции Н.Д. Кузнецова упрочнялось до 70% всех деталей, в том числе: 94% – компрессора, 90% – деталей трубопроводов, 46% – турбины. Для примера рассмотрим обработку деталей дробью, как наиболее часто применяемую в авиастроении, так как она позволяет упрочнять детали различной формы и размеров. На рисунке 4.27 показана схема упрочнения дробью. Обрабатываемая деталь совершает вращательное и возвратно-поступательное движения. В среде воздуха или жидкости (масло, керосин, вода) на деталь направляется поток дроби (шариков). Дробь, ударяет о поверхность и вызывает пластические деформации, в результате которых, в поверхностном слое детали, возникают сжимающие остаточные напряжения. Остаточные напряжения, складываясь с растягивающими рабочими, уменьшают последние, что приводит к повышению сопротивления усталости, так как цикл напряжений, смещается в область сжимающих средних напряжений, при которых увеличивается предельная амплитуда цикла. В результате суммирования, увеличиваются и сжимающие напряжения, однако, усталостная трещина распространяется, только под действием растягивающих напряжений, поэтому, увеличение сжимающих напряжений, не приводит к снижению сопротивления усталости.
При использовании других методов ППД механизм упрочнения поверхностного слоя деталей, аналогичен рассмотренному. Металлургические мероприятия сводятся к наиболее оптимальному выбору материала и термообработки, устранению закалочных трещин, усадочных раковин, газовых пузырей и включений. Сюда же может быть отнесена химико-термическая обработка, повышающая сопротивление усталости, за счёт создания в поверхностном слое деталей, сжимающих остаточных напряжений. Эксплуатационные мероприятия включают в себя защиту поверхности от коррозии (окраска, смазка), предохранение наиболее напряжённых и ответственных деталей от повреждений (царапины, забои при сборке и разборке, истирание), предотвращение сверхнормативных перегрузок машин, обеспечение плавного пуска и остановок, предупреждение загрязнения рабочих поверхностей и связанных с этим, явлений износа, задиров. Профилактические мероприятия предусматривают периодическое освидетельствование деталей с помощью современной дефектоскопической техники, смазку трущихся и замену износившихся деталей. Использование всех рассмотренных мероприятий позволяет существенно повысить сопротивление усталости деталей, что влечёт за собой, увеличение ресурса и надёжности авиационной и космической техники. Вопросы для самопроверки 1. По каким причинам могут циклически изменяться напряжения в деталях? 2. В чём заключаются особенности сопротивления материалов действию циклически изменяющихся напряжений? 3. Как происходит разрушение деталей под действием циклически изменяющихся напряжений? 4. В чём заключается явление усталости? 5. Перечислите характеристики цикла переменных напряжений. 6. Как рассчитываются амплитуда и среднее напряжение цикла переменных напряжений? 7. Перечислите и нарисуйте разновидности циклов переменных напряжений. 8. Что называют пределом выносливости материала? Как его обозначают? 9. В чём заключается опытное определение предела выносливости материала при симметричном цикле изгиба? 10. Какой график, называют кривой усталости? Как его строят? 11. Какие циклы называют предельными? Как обозначаются параметры предельного цикла? 12. Как оценивают сопротивление усталости материала по диаграмме предельных амплитуд? 13. С какой целью и как проводят схематизацию диаграмм предельных амплитуд цикла напряжений для материала? 14. Каков порядок построения схематизированной диаграммы предельных амплитуд цикла для материала? 15. Какие отличия детали от стандартного образца учитывают при определении предела выносливости детали? 16. Как определяют коэффициент снижения предела выносливости детали? 17. Что такое концентрация напряжений? 18. Что показывает теоретический коэффициент концентрации напряжений? Как его определяют? 19. Что показывает эффективный коэффициент концентрации напряжений и как он влияет на предел выносливости детали? 20. Как влияют абсолютные размеры детали на её предел выносливости? 21. Как влияет состояние поверхности на предел выносливости детали? Как учитывают это влияние в расчётах на прочность? 22. Какие виды обработок называют упрочняющими и как учитывают их влияние на предел выносливости детали? 23. Как записывается условие прочности (в общем виде) при действии циклически изменяющихся напряжений? 24. Что представляют собой коэффициенты запаса по усталости и по текучести? Как определяют их графическим путём? 25. Как подсчитывают коэффициенты запаса по усталости и по текучести при линейном напряжённом состоянии и чистом сдвиге? 26. Как подсчитывают коэффициенты запаса по усталости и по текучести в случае сложного напряжённого состояния? 27. Какие мероприятия используют для повышения сопротивления усталости деталей? КОЛЕБАНИЯ УПРУГИХ СИСТЕМ Основные понятия об упругих колебаниях Если упругую конструкцию или деталь, соединённую с конструкцией, вывести из положения равновесия и освободить, то она будет совершать собственные колебания. В детали будут действовать переменные напряжения. В этом случае усталостное разрушение не произойдёт, так как колебания, быстро затухают. Другое дело, когда на деталь действуют, периодически изменяющиеся силы. При этом, переменные напряжения, не затухают, и может произойти усталостное разрушение. Особенно велика опасность, при резонансном режиме, когда частота изменения силы совпадает с собственной частотой колебаний детали. При резонансе, даже небольшие переменные силы, вызывают в детали, большие переменные напряжения. Поэтому нужно проектировать деталь таким образом, чтобы её собственная частота колебаний, значительно отличалась, от частоты изменения силы. В двигателях летательных аппаратов, например, периодически изменяющихся сил чрезвычайно много, имеется широкий спектр возмущающих частот, поэтому, уйти от резонанса не удаётся. Нам предстоит решить две задачи: 1) определить частоту собственных колебаний, чтобы выяснить, будет ли резонанс, в конструкции; 2) определить переменные напряжения при колебаниях, чтобы вычислить коэффициент запаса детали по усталостному разрушению. Число степеней свободы упругого тела – определяется наименьшим числом независимых координат, которые вполне определяют, положение тела при колебаниях (движении). Это, фундаментальное понятие. В принципе, любая деформируемая конструкция, (тело) – система с бесконечным числом степеней свободы, так как, строго говоря, расстояние между точками тела, может изменяться. А практически, проще – конструкция состоит из нескольких частей с большой массой и жёсткостью, соединённых, между собой, деталями с небольшой массой и жёсткостью. Поэтому, достаточно знать ограниченное число степеней свободы. Приведём примеры: Пример 1 (рис. 5.1, а). Масса пружины мала по сравнению с массой т груза, поэтому, эту систему можно считать системой с одной
степенью свободы. Пример 2 (рис. 5.1, б). Масса каждого груза m 1 и т 2 значительно больше массы балки, а для составления уравнений движения при колебаниях, достаточно знать прогибы ξ 1 и ξ 2. Это, система с двумя степенями свободы. 5.2. Собственные колебания системы Изобразим систему с одной степенью свободы (рис. 5.2, а). Предстоит установить закон движения и формулу для частоты собственных колебаний. Вспомним принцип Даламбера, из теоретической механики. Как он выглядит, применительно к упругим системам? Отрежем груз и покажем его, отдельно (рис. 5.2, б).
. До сих пор мы были знакомы с податливостью – 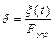 . Сравнивая, видим, что . Сравнивая, видим, что 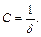
Запишем уравнение движения груза – Правило применения принципа Даламбера применительно к упругим системам: Если упругую систему остановить и к действующим силам (в нашем случае, их нет) добавить силы инерции, то наблюдаемое перемещение можно рассматривать, как результат статического действия суммы этих сил. Теперь составим уравнение движения груза, используя принцип Даламбера (покажем на рисунке 5.2, а силу инерции F и).
тогда
– дифференциальное уравнение колебания системы с одной степенью свободы. Как решить это дифференциальное уравнение? Составляем характеристическое уравнение и находим его корни. Если проделать всё это,
где А – амплитуда свободных колебаний; φ – начальная фаза колебаний; Для расчёта на прочность А и φ интереса не представляют, поэтому остановимся на ω.
– универсальная формула для определения частоты собственных колебаний системы с одной степенью свободы – это круговая скорость вращения вектора, изображающего колебание. Здесь: g – ускорение свободного падения (силы тяжести); ξ ст – перемещение системы, вызванное статическим действием силы, равной силе веса груза, приложенной по направлению колебаний. Частота собственных колебаний системы (в герцах) определяется формулой
5.3. Собственные колебания системы Это реальная задача, так как в реальных конструкциях. есть силы сопротивления, которые бывают либо внешними, либо внутренними. Внешние силы сопротивления – сопротивление воздуха, например, сопротивление, которую оказывает воздух лопатке компрессора, при её колебаниях – пропорционально квадрату скорости. Сопротивление масляного слоя (например, в подшипниках скольжения) – пропорционально скорости в первой степени – это, так называемое, вязкое сопротивление. Сила сопротивления при сухом трении, от скорости не зависит, а зависит, от давления. Внутренние силы сопротивления – они всегда есть и связаны с рассеянием энергии в материале, поэтому называются силами внутреннего трения. Они обусловлены силами, необходимыми для перемещения дислокаций. Силы внутреннего сопротивления, от скорости не зависят, а зависят, только от напряжений. Наиболее подробно разработана математическая теория колебаний при вязком сопротивлении. Все другие случаи сил сопротивления, обычно приводятся к вязкому сопротивлению, то есть математическая теория колебаний, разработанная для вязкого сопротивления, применяется, и для других видов сопротивления. Изобразим систему с одной степенью свободы (рис. 5.3). Груз массой т, может перемещаться в направляющих. Нужно найти ξ (t), то есть закон, по которому изменяется перемещение, с течением времени. Воспользуемся принципом Даламбера. Для этого к действующим силам добавляем силу инерции и останавливаем систему.
После этого, останавливаем систему, и определяем перемещение в наблюдаемый момент времени, как результат статического действия всех сил. Следовательно, перемещение ξ (t) вызвано этими двумя силами, поэтому ξ = δ· (R + Fu), здесь δ – податливость системы – перемещение от силы, равной единице. Далее подставим значения сил и проведём преобразования
Обозначим α/ m = 2· n, где п – параметр затухания колебаний – он характеризует влияние сил сопротивления на собственные колебания;
– дифференциальное уравнение затухающих колебаний (собственные колебания с затуханием). Это линейное однородное дифференциальное уравнение с постоянными коэффициентами. Характеристическое уравнение
Будем рассматривать случай сравнительно небольших сил сопротивления, когда п 2 < ω 2 тогда r 1, 2 = – n ± i ·ω i, где
Проанализируем полученное выражение. По аналогии с собственными колебаниями без затухания, величину, стоящую перед синусом, называют амплитудой затухающих колебаний ω 1 – частота собственных колебаний при наличии сил сопротивления В нашем случае, две неизвестные величины С и φ. Они определяются из начальных условий: при t = 0 ξ = ξ о, ξ´ = ξ´ о, например, отводим груз и отпускаем, тогда ξ о = ξ´ о = 0. Для расчётов на прочность, эти величины не нужны.
Отношение амплитуд может служить характеристикой влияния сил сопротивления, на затухающие колебания. Этой характеристикой (e пТ) пользоваться неудобно, поэтому рассматривается, не отношение амплитуд, а логарифм этого отношения, и обозначается λ – логарифмический декремент колебаний.
Теперь изобразим график изменения перемещений (рис. 5.4), то есть график функции (5.1). Величину λ довольно часто определяют по таким графикам, построенным по результатам опытов. Далее, вернёмся к частоте собственных колебаний при наличии сил сопротивления Проведём оценку на примере: пусть At / At + T = 2, то есть Таким образом, несмотря на то, что силы сопротивления большие, разница между частотами, практически нет и, влиянием сил сопротивления, на частоту собственных колебаний системы можно пренебречь. Тогда
5.4. Вынужденные колебания системы с одной степенью Это основной, наиболее интересный случай.
Изобразим систему (рис. 5.5). На тело действует возмущающая периодическая сила F (t) = F 0·cos Ω t, где F 0 – амплитуда возмущающей силы, Ω – круговая частота изменения возмущающей силы. Пример возмущающей силы – несбалансированная масса ротора турбомашины. Мы ограничимся случаем простой гармоники, а если случай сложный, то нужно разложить в ряд Фурье. Необходимо составить уравнение движения груза. Для этого снова воспользуемся принципом Даламбера. К действующим силам добавим силу инерции (F и), остановим систему (подчеркнём, что сила сопротивления. приложена непосредственно к грузу, а не к связи) и считаем ξ (t) как результат статического действия суммы всех этих сил. ξ (t) = δ· [ R + Fu + F (t)], разделим на податливость δ, подставим значения сил и произведём преобразования
Обозначим α/ m = 2· n, – дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы. Сравниваем его с уравнением предыдущего раздела – они отличаются только правой частью, то есть это неоднородное дифференциальное уравнение. Его решение ищется в виде ξ = ξ одн + ξ частн, где ξ одн ξ частн ищем в виде ξ частн = M ·sin Ω· t + N ·cos Ω· t. Для определения M и N подставляем ξ частн в исходное дифференциальное уравнение. Запишем окончательное решение, объединив его в одной гармонике
где Ω – круговая частота вынужденных колебаний, то есть частота вынужденных колебаний совпадает с частотой возмущающей силы; ψ – начальная фаза колебаний – разность фаз перемещений и возмущающей силы, следовательно, перемещение отстаёт от возмущающей силы, на угол ψ. В расчётах на прочность, она не нужна. Преобразуем формулу для амплитуды вынужденных колебаний
Обозначим
Выясним физический смысл отношения
ξ ст – перемещение от статической силы, равной силе веса груза, приложенной по направлению колебаний; А 0 – равновесная амплитуда. Физический смысл – перемещение, которое вызывается статическим действием силы, равной амплитуде возмущающей силы. Обозначим
А = β· А 0.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.156.75 (0.118 с.) |
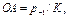
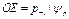 .
.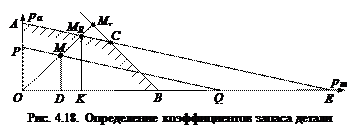



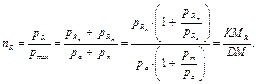
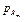 без знака абсолютной величины.
без знака абсолютной величины.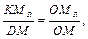 тогда
тогда
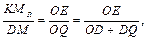
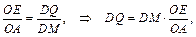 тогда
тогда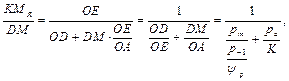 отсюда
отсюда
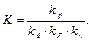



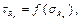 то есть, как влияют напряжения изгиба, на предельные напряжения при кручении. Две точки диаграммы известны до проведения испытаний на усталость при сложном напряжённом состоянии (рис. 4.21):
то есть, как влияют напряжения изгиба, на предельные напряжения при кручении. Две точки диаграммы известны до проведения испытаний на усталость при сложном напряжённом состоянии (рис. 4.21):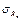 = 0,
= 0, 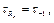 то есть имеет место, только кручение,
то есть имеет место, только кручение,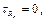
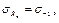 то есть имеет место, только изгиб.
то есть имеет место, только изгиб.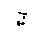
 Для получения каждой промежуточной точки испытывается партия стандартных лабораторных образцов. Напряжения изгиба в каждой партии одинаковы, а напряжения кручения изменяются. Определяется
Для получения каждой промежуточной точки испытывается партия стандартных лабораторных образцов. Напряжения изгиба в каждой партии одинаковы, а напряжения кручения изменяются. Определяется  для заданного напряжения изгиба и строится диаграмма предельных амплитуд циклов. Кривая оказывается близкой к эллипсу, поэтому её можно представить аналитически:
для заданного напряжения изгиба и строится диаграмма предельных амплитуд циклов. Кривая оказывается близкой к эллипсу, поэтому её можно представить аналитически: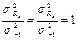 – уравнение предельной кривой
– уравнение предельной кривой 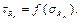 Установлено, что эта зависимость достаточно хорошо подтверждается для многих материалов.
Установлено, что эта зависимость достаточно хорошо подтверждается для многих материалов.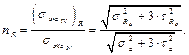
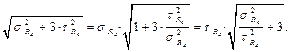
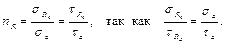
 с помощью уравнения предельной кривой: для этого первое слагаемое делим на σа, а второе – на τа
с помощью уравнения предельной кривой: для этого первое слагаемое делим на σа, а второе – на τа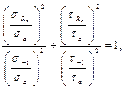
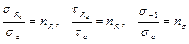 – парциальный коэффициент запаса по нормальным напряжениям,
– парциальный коэффициент запаса по нормальным напряжениям, 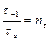 – парциальный коэффициент запаса по касательным напряжениям, тогда
– парциальный коэффициент запаса по касательным напряжениям, тогда 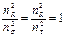 или
или  далее, разрешив зависимость относительно п r, получим
далее, разрешив зависимость относительно п r, получим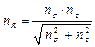
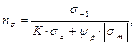
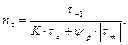

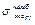 , когда силы изменяются не синфазно? Для этого нужно определить
, когда силы изменяются не синфазно? Для этого нужно определить 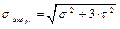 и построить график изменения
и построить график изменения 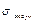 (рис. 4.22) по времени. Так поступают, в общем случае.
(рис. 4.22) по времени. Так поступают, в общем случае. При синфазном изменении нормальных и касательных напряжений график строить не нужно. В этом случае
При синфазном изменении нормальных и касательных напряжений график строить не нужно. В этом случае Напряжения взяты по абсолютной величине, так как может быть изменение напряжений в противофазе.
Напряжения взяты по абсолютной величине, так как может быть изменение напряжений в противофазе.


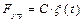 – сила упругости пропорциональна отклонению от положения равновесия,
– сила упругости пропорциональна отклонению от положения равновесия, 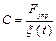 – жёсткость связи (в данном случае, пружины) – это сила, вызывающая единичное перемещение
– жёсткость связи (в данном случае, пружины) – это сила, вызывающая единичное перемещение 
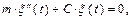 тогда
тогда 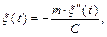 но
но 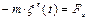 и уравнение движения груза примет вид
и уравнение движения груза примет вид 

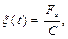
 – здесь жёсткость представлена через эффект действия груза, ξ ст – перемещение, вызванное силой, равной силе веса груза, приложенной по направлению колебаний,
– здесь жёсткость представлена через эффект действия груза, ξ ст – перемещение, вызванное силой, равной силе веса груза, приложенной по направлению колебаний,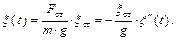 Отсюда
Отсюда
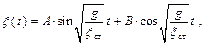 свернув это уравнение получим
свернув это уравнение получим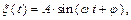
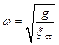 – круговая частота собственных колебаний с одной степенью свободы. А и φ находятся из начальных условий: при t = 0 ξ = ξ о, ξ´ = ξ´ о.
– круговая частота собственных колебаний с одной степенью свободы. А и φ находятся из начальных условий: при t = 0 ξ = ξ о, ξ´ = ξ´ о.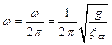 .
.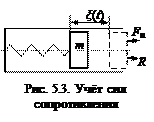 Действующая сила – сила сопротивления (сила вязкого сопротивления) –
Действующая сила – сила сопротивления (сила вязкого сопротивления) – 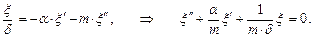
 – круговая частота собственных колебаний системы, при отсутствии сил сопротивления. Окончательно получим
– круговая частота собственных колебаний системы, при отсутствии сил сопротивления. Окончательно получим
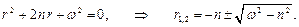
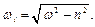 Имея корни, можно записать решение уравнения
Имея корни, можно записать решение уравнения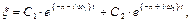
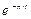 вынесем за скобку и выразив через тригонометрические функции, получим
вынесем за скобку и выразив через тригонометрические функции, получим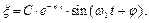 (5.1)
(5.1)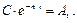
 то есть ω 1 < ω и, чем больше силы сопротивления, тем больше, эта разница, φ – начальная фаза колебаний.
то есть ω 1 < ω и, чем больше силы сопротивления, тем больше, эта разница, φ – начальная фаза колебаний.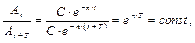 то есть отношение любых двух амплитуд, следующих, одна за другой, через период, есть величина постоянная. Эти амплитуды составляют геометрическую прогрессию.
то есть отношение любых двух амплитуд, следующих, одна за другой, через период, есть величина постоянная. Эти амплитуды составляют геометрическую прогрессию. Как вычислить период колебаний?
Как вычислить период колебаний?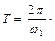
 получим:
получим:  тогда
тогда  или
или 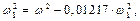 следовательно, ω 1 = 0.9940 ω.
следовательно, ω 1 = 0.9940 ω.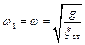 .
.
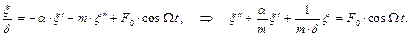
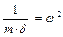 и окончательно получим
и окончательно получим
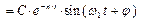 . С течением времени ξ одн уменьшается и поэтому этим слагаемым пренебрегают, тогда ξ = ξ частн.
. С течением времени ξ одн уменьшается и поэтому этим слагаемым пренебрегают, тогда ξ = ξ частн.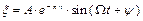 ,
,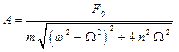 – амплитуда вынужденных колебаний;
– амплитуда вынужденных колебаний;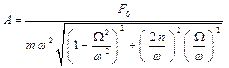
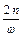 = γ – коэффициент демпфирования. Этот коэффициент, так же, как и λ характеризует влияние сил сопротивления на колебания. Установим связь между γ и λ
= γ – коэффициент демпфирования. Этот коэффициент, так же, как и λ характеризует влияние сил сопротивления на колебания. Установим связь между γ и λ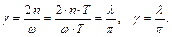

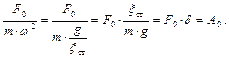
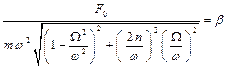
 – коэффициент усиления колебаний или динамический коэффициент, тогда
– коэффициент усиления колебаний или динамический коэффициент, тогда


