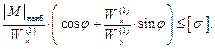Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий случай сложного сопротивления бруса
3.1.1. Напряжения и расчёт на прочность
Покажем кривой брус произвольного поперечного сечения, нагруженный произвольными самоуравновешенными силами. На рис. 3.1 показаны и активные силы, и реакции связей. Рассмотрим внутренние силы в поперечном сечении бруса. Применим метод сечения, секущая плоскость перпендикулярна оси бруса.
Левую часть бруса отбрасываем и изображаем правую (рис. 3.2, а). С – центр тяжести сечения. Покажем главные центральные оси сечения. Ось z – касательная к оси бруса, оси х, у – главные центральные оси поперечного сечения. Как отброшенная часть действует на оставшуюся? Распределённые касательные и нормальные силы приводим к центру тяжести сечения С. В результате получим главный вектор и главный момент. Покажем компоненты главного вектора: N, Qx, Qy и компоненты главного момента: – М к, Мх, Му. Рассмотрим составляющие: 1) N – нормальная сила, вызывает центральное растяжение или сжатие; 2) М к – крутящий момент, вызывает кручение; 3) Qy, Мх – поперечная сила и изгибающий момент, вызывают поперечный изгиб в плоскости наибольшей жёсткости; 4) Qx, My – поперечная сила и изгибающий момент, вызывают поперечный изгиб в плоскости наименьшей жёсткости. Подводим итог: деформацию в общем случае сложного сопротивления можно представить в виде суммы четырёх простых деформаций: центрального растяжения или сжатия, кручения, изгиба в плоскости наибольшей жёсткости и изгиба в плоскости наименьшей жёсткости. Простые деформации мы изучали, поэтому, будем применять принцип суперпозиции. Правила знаков для внутренних сил те же, что и при простых деформациях. Силы считаются положительными, если они совпадают с положительными направлениями осей, а пары сил положительны, если они направлены против часовой стрелки при взгляде со стороны положительного направления оси. На рис. 3.2, а показаны положительные направления внутренних сил. Как вычислить силы и пары сил? Нужно все силы привести к центру тяжести сечения и использовать уравнения равновесия рассматриваемой части бруса.
Перейдём к напряжениям. Рассмотрим любую точку А (при выводе – в первой четверти), х, у – координаты точки А, в которой определяем σ и τ. Приступим к выводу формулы. Применяем принцип суперпозиции: где Подставляв общую формулу, получим
– формула для нормальных напряжений в поперечном сечении бруса в общем случае сложного сопротивления. Далее, касательные напряжения. Здесь, дело обстоит сложнее. Хотя слагаемые и лежат в одной плоскости, но по направлению, они не совпадают, поэтому необходимо рассмотреть векторную величину: Эти напряжения нужно суммировать геометрически. В общем случае, довести до модуля невозможно. Будем это делать, в частных случаях. Перейдём к оценке прочности. Вырежем элемент, одна пара граней которого, перпендикулярна τ, а вторая – перпендикулярна оси бруса. Изобразим элемент, если смотреть на него по направлению В (см. рис. 3.2, б). На горизонтальной грани нормальных напряжений нет, так как при любой простой деформации, волокна не надавливают друг на друга. На передней грани напряжений нет. Отсюда, в общем случае нагружения, в любой точке бруса имеет место плоское напряжённое состояние. Далее, условие прочности: σ экв ≤ [ σ ]. Чаще всего, мы имеем дело со стальными, алюминиевыми, бронзовыми брусьями (то есть, пластичными материалами), поэтому применяем IV теорию предельных напряжённых состояний.
– условие прочности всего бруса. Как найти самую опасную точку бруса? В общем случае сложного сопротивления, это достаточно сложно. В некоторых частных случаях сложного сопротивления (изгиб с растяжением или сжатием, косой изгиб, внецентренное растяжение или сжатие, изгиб с кручением) это представляется возможным.
3.1.2. Перемещения бруса в общем случае Изобразим кривой брус (показана только ось) (рис. 3.3, а).
Под действием нагрузок брус перемещается – пунктиром показано положение бруса после нагружения (конечно в конструкциях, таких больших перемещений не бывает). ∆ k. – полное перемещение точки k, в данном случае – линейное. Для изображённого нагружения можно вычислить N, M х, M у. M к (перемещения от поперечных сил пренебрежимо малы), предварительно выбрав направление осей х, у и z (рис. 3.3, в). Затем рассмотрим единичное нагружение этого бруса (рис. 3.3, б), причём мы не знаем направления полного перемещения, поэтому определим перемещение в направлении b – ∆ b. Без вывода, запишем интеграл Мора в общем случае нагружения бруса. Эта формула получается по аналогии формулы для изгиба. Формула Мора применима и к брусьям большой кривизны.
– это обобщенный интеграл Мора. Здесь N, Мх, Му, М к – внутренние усилия, от которых нужно найти перемещение;
Е·А, Е· Jx, E · Jy, G · J к – жёсткости бруса при соответствующих простых деформациях. Как же найти полное перемещение? Для этого определяем перемещение в трёх взаимно перпендикулярных направлениях: ∆ x, ∆ y, ∆ z, a полное перемещение определяем как геометрическую сумму Рассмотрим, как упрощается формула Мора в частных случаях. 1 частный случай. Балки или плоские рамы – плоские неизменяемые системы стержней, связанных между собой и нагруженных в своей плоскости. В этом случае М к = Му = 0,
2 частный случай. Пространственный брус или плоско-пространственная рама или пространственная рама – неизменяемые система плоских стержней, связанных между собой и нагруженных не только в своей плоскости, но и в плоскости, перпендикулярной плоскости рамы. В этом случае Мх ≠ 0, Му ≠ 0, М к ≠ 0
3 частный случай. Шарнирно-стержневая ферма. В реальных случаях стержни склёпаны, но расчёт производится с достаточной точностью по шарнирной схеме. В этом случае Мх = Му = М к = 0, N ≠ 0 и
Обычно N в пределах каждого стержня не меняется, поэтому формулу можно упростить.
3.2. Расчёт плоских статически неопределимых рам Рамой называется геометрически неизменяемая система связанных между собой стержней, которая сопротивляется внешним силам главным образом посредством изгиба и кручения. Бывают ещё системы стержней, которые сопротивляется внешним силам главным образом посредством растяжения-сжатия – это фермы – они не входят в рассматриваемый вопрос. Если оси стержней и внешние силы лежат в одной плоскости, то такую раму называют плоской. Если оси стержней лежат в одной плоскости, а внешние силы – в другой, то такую раму называют плоско-пространственной. Если оси стержней и внешние силы не лежат в одной плоскости, то такую раму называют пространственной. Мы остановимся, на рассмотрении плоских рам. Рамы бывают статически определимыми и статически неопределимыми.
Рассмотрим статически определимые рамы. В раме (рис. 3.4, а) неизвестных три и уравнений статики тоже три. В следующей раме (рис. 3.4, б) неизвестных четыре и уравнений статики тоже четыре (ещё одно уравнение, даёт шарнир). Существуют два вида статической неопределимости: внешняя статическая неопределимость и внутренняя статическая неопределимость. Рама с внешней статической неопределимостью, если в качестве лишних неизвестных можно подобрать внешние, для рамы, силы, например, реакции опор. В раме, показанной на рисунке 3.4, в, в шесть неизвестных и три уравнения статики, то есть рама три раза статически неопределимая.
Теперь в любом сечении рамы можно вычислить внутренние силы через Х 1, Х 2 и Х 3. Для определения неизвестных сил Х 1, Х 2 и Х 3 используется метод сил.
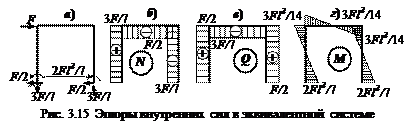
В раме, представленной на рис. 3.6, проведём произвольное сечение а – а, отбросим нижнюю часть и изобразим то, что осталось. Приведём внутренние силы к центру тяжести сечения. Они приводятся к главному вектору с составляющими Q – в плоскости сечения, N – по нормали к сечению, и к главному моменту M. N – нормальная сила, N > 0 – при растяжении, N < 0 – при сжатии. Q – поперечная сила, Q > 0, если внешняя сила вращает рассматриваемую часть рамы по часовой стрелке (как и для балок), Q < 0, если внешняя сила вращает рассматриваемую часть рамы против часовой стрелке. M – изгибающий момент. При расчёте рам, М рассматривается как арифметическая величина, а эпюру изгибающих моментов, строят на сжатых волокнах. Величину внутренних сил определяют, как и раньше, из уравнений равновесия рассматриваемой части рамы. Следовательно, рама испытывает сложное сопротивление, состоящее из плоского поперечного изгиба в плоскости рамы и центрального растяжения или сжатия. Большая группа элементов летательных аппаратов и их двигателей являются рамами. Например, шпангоут является рамой с внутренней статической неопределимостью.
1) связь, передающая нормальную силу N; 2) связь, передающая поперечную силу Q; 3) связь, передающая изгибающий момент М.
Как устранить эти связи при расчёте рам методом сил? Примеры устранения различных связей приведены на рисунке 3.8. 3.2.1 Пример расчёта плоской
Имеем шесть неизвестных (Н A, V A, MA, НВ, VВ, MВ). Статика даёт три уравнения. Таким образом, в данном случае три лишних неизвестных, то есть, рама три раза статически неопределима. Для раскрытия статической неопределимости воспользуемся методом сил. Вначале назначим три лишних неизвестных, но при этом основная система должна быть геометрически неизменяемой. При анализе, сама система, считается абсолютно жёсткой.
Сделаем первую попытку. Примем за лишние неизвестные (Н A, НВ, MВ). Изобразим систему с отброшенными лишними связями (рис. 3.10, а). Такое закрепление препятствует только вертикальному перемещению и повороту. Теперь смотрим – является ли система неизменяемой? Нет, так как она может перемещаться в горизонтальном направлении. Поэтому, назначать таким образом, лишние неизвестные нельзя, так как такую систему, нагрузить невозможно. Сделаем вторую попытку. За лишние неизвестные примем (М A, VВ, MВ). Изобразим систему с оставшимися связями (рис. 3.10, б). Основная система должна быть неизменяемой, не только в конечной, но и в бесконечно малой форме. Выбранная система является мгновенно изменяемой, так как может быть поворот опоры В на бесконечно малый угол вокруг опоры А. Для метода сил, мгновенно изменяемая система не годится, так как мгновенно изменяемые системы нелинейные, то есть перемещения в них, зависят от действующих сил нелинейно, а при выводе канонических уравнений метода сил, предполагалась линейная зависимость. Если одна из стоек выше или ниже другой, то мгновенной изменяемости системы не будет. Сделаем третью попытку. За лишние неизвестные примем Далее изображаем эквивалентную систему (рис. 3.11), для чего выбранную основную систему нагружаем активной силой и неизвестными силами (Х 1 = НВ, Х 2 = V В, Х 3 = MВ). Она в точности воспроизводит исходную систему.
Определяем коэффициенты и свободные члены канонических уравнений. Воспользуемся общими формулами для интегралов Мора.
На прямолинейных участках, интегралы Мора вычислим способом Верещагина. Для этого, выбранную основную систему последовательно нагружаем необходимыми единичными и внешними силами и строим эпюры изгибающих моментов
Теперь есть все необходимые эпюры и можно вычислить коэффициенты и свободные члены канонических уравнений. Вычислим их значения способом Верещагина
Аналогично вычисляются остальные коэффициенты и свободные члены.
Умножив канонические уравнения на E · J,подставим в них значения коэффициентов и свободных членов и раскроем статическую неопределимость
Обращаем внимание на знак неизвестных: Х 2 и Х 3 – направление правильное, Х 1 – направлено в противоположную сторону.
Таким образом, найдены все силы, действующие на раму. Прежде чем строить эпюры внутренних силовых факторов (N, Q, M), необходимо сделать проверку. Обычно, вначале делается частная проверка – вычисленные значения Х 1, Х 2, Х 3 подставляются во все канонические уравнения и убеждаются, что уравнения обращаются Затем делается генеральная (общая) проверка. В расчётах на прочность всегда делаются несколько проверок, так как расчёты менее трудоёмкие и менее затратные, по сравнению с изготовлением конструкций. Генеральная проверка.
Для генеральной проверки выбирается новая основная система (НОС) (рис. 3.14, а). Для этого необходимо взять все новые лишние связи. В нашем случае, за новые лишние связи примем связи на левой опоре. Показываем новую эквивалентную систему (НЭС) и перемещения в направлении новых неизвестных (рис. 3.14, б). Эти перемещения в эквивалентной системе должны быть равны нулю.
Однако из-за погрешностей вычислений в большинстве случаев добиться нулевого результата не удаётся. Поэтому более удобно разделить силы на активные и реактивные (реакции отброшенных связей), определить перемещения в основной системе отдельно от активных сил ∆i А (рис. 3.14, в) и отдельно от реактивных сил ∆ iR
Если такие соотношения выполняются по всем новым перемещениям, то статическая неопределимость раскрыта верно. Теперь строим в эквивалентной системе (рис. 3.15, a) эпюры внутренних силовых факторов (N, Q, M) (рис. 3.15, б-в) и проводим расчёт на прочность.
– условие прочности для любого сечения. Поскольку
– условие прочности для всей рамы.
Расчёт на прочность
Это условие прочности для всей рамы и так решается первая задача сопротивления материалов. Здесь N – нормальная сила в сечении, где действует | М| наиб. Вторая задача – подбор размеров поперечного сечения – приводится из условия прочности при изгибе
Затем подобранное сечение проверяется по полному условию прочности. Третья задача – определение грузоподъёмности – эта задача решается только в каждом конкретном случае. Косой изгиб 3.3.1. Напряжения и расчёт на прочность Вспомним плоский изгиб. Брус (рис. 3.17, а) испытывает плоский изгиб, так как прогибы лежат в плоскости изгибающих сил (в плоскости полного изгибающего момента). Теперь, о косом изгибе (рис. 3.17, б). Брус испытывает косой изгиб, если он нагружен силами, перпендикулярными его оси и парами сил, плоскость действия которых не совпадает ни с одной из главных плоскостей жёсткости бруса.
Изобразим поперечное сечение бруса, покажем его главные центральные оси и плоскость полного изгибающего момента. При таком изгибе, плоскость перемещений не совпадает с плоскостью полного изгибающего момента. Приступим к выводу формулы для напряжений. Будем рассматривать частный случай, но формулу получим для общего случая. Рассмотрим консольную балку, нагруженную силой и произвольное сечение этой балки. С – центр тяжести поперечного сечения
Представим косой изгиб как сумму простых деформаций. Для этого разложим силу на составляющие Fx и Fy: Fx = F ·sin φ, Fy = F ·cos φ. Каждая составляющая вызывает плоский поперечный изгиб: Fx – в плоскости наименьшей жёсткости, a Fy – в плоскости наибольшей жёсткости бруса. Применим принцип суперпозиции
Далее подставляем в исходную формулу значения компонент и получаем
Здесь F · z · = M – полный изгибающий момент, тогда
Это почти окончательная формула. Почему? Знак изгибающего момента может быть и положительным, поэтому в формуле нужно поставить два знака
Здесь M – полный изгибающий момент в рассматриваемом сечении, берётся по абсолютной величине, а знак перед M должен совпадать со знаком напряжений в первой четверти; х, у – координаты точки, в которой определятся напряжение φ – угол между плоскостью полного изгибающего момента и плоскостью наибольшей жёсткости бруса; Jx, Jy – главные центральные моменты инерции поперечного сечения бруса. Таким образом, мы получили общую формулу для нормальных напряжений при косом изгибе для любых сил. Теперь переходим к расчёту на прочность при косом изгибе. Рассмотрим некоторые предварительные соображения. При плоском изгибе соседние сечения поворачиваются относительно главной оси. При косом изгибе соседние сечения взаимно поворачиваются относительно двух осей, из теоретической механики известно, что они поворачиваются относительно некоторой одной (нейтральной) оси. Найдём нейтральную ось при косом изгибе. На ней σ = 0, так как волокна не изменяют своей длины, х 0, у 0 – координаты нейтральной оси. Представим их в формулу, тогда σ должно быть равно нулю.
Видно, что это уравнение прямой, свободных членов нет, поэтому это прямая, проходящая через начало координат. Запишем уравнение нейтральной оси в изменённом виде
Теперь изобразим поперечное сечение с плоскостью полного изгибающего момента и разберёмся, как на сечении расположена нейтральная ось (рис. 3.19). Для прямой, проходящей через начало координат Для определения положения нейтральной оси удобнее пользоваться смежным углом α, но tg α = – tg β, тогда
– формула для определения положения нейтральной оси. Из этой формулы видно, что α > φ, так как Jx > J y (об этом мы договорились, при изучении геометрических характеристик плоских сечений). Следовательно, если плоскость действия изгибающего момента поворачивается от плоскости наибольшей жёсткости на угол φ, то нейтральная ось поворачивается от плоскости наименьшей жёсткости в том же направлении на угол α > φ Если Jx = Jy, то α = φ, но в этом случае, при любом φ будет плоский изгиб, так как все центральные оси сечения, будут главными. Для чего мы искали положение нейтральной оси? Зная положение нейтральной оси, можно найти наиболее напряжённую точку сечения – это будет наиболее удалённая, от нейтральной оси, точка. Её можно найти, проведя касательные к контуру сечения, параллельные нейтральной оси. Пусть это будет точка 1 (см. рис. 3.19), тогда
– условие прочности для произвольного сечения балки при косом изгибе. Как им пользоваться? Во первых, нужно определить угол α, построить нейтральную ось, затем, проведя касательные к контуру сечения, параллельные нейтральной оси, определить коордитаты точки 1 (см. рис. 3.19). Только после этого, подставив эти координаты в условие прочности, можно оценить прочность. Рассмотрим частный случай, когда φ = const по длине бруса (балки) и тогда координаты наиболее удалённой от нейтральной оси точки по длине бруса не меняются. Тогда, второй множитель не меняется и наиболее опасным будет сечение, где действует М наиб, поэтому условие прочности для всей балки запишется следующим образом
Теперь в рамках этого частного случая (φ = const), рассмотрим сечения, которые имеют две оси симметрии и выступающие острые углы (рис. 3.20). Вне зависимости от положения нейтральной оси, касательные к ней, будут проходить через диагональные угловые точки и | х 1| = | х 2| = | х 3| = | х 4| = | х | наиб; | у 1| = | у 2| = | у 3| = | у 4| = | у | наиб. Если ещё учесть, что
– это условие прочности при косом изгибе для балок, поперечные сечения которых имеют две оси симметрии и выступающие острые углы и, конечно, для частного случая, когда φ = const. Здесь круглые скобки, так как все величины в скобках, положительные, Далее рассмотрим, как решаются три задачи сопротивления материалов при косом изгибе? 1 задача – проверка прочности.
Здесь всё выражено в явном виде. 2 задача – назначение размеров поперечного сечения. Разрешим условие прочности относительно Wx
В явном виде формула неразрешима, так как Wx есть и в правой части, но и это не главное. В правой части есть ещё Wy, который зависит от Wx через форму и размеры сечения. Поэтому размеры поперечного сечения назначаются методом попыток. Для первой попытки принимают среднее значение (Wx / Wy) ср для балок рассматриваемого профиля. Для двутавровых балок, например, (Wx / Wy) ср ≈ 10, а для прямоугольных сечений – (Wx / Wy)ср= (h / b)2
Теперь, зная
Как правило, первая попытка не бывает удачной. Условие прочности не выполняется, в ту или другую сторону: либо левая часть больше правой, либо левая часть заметно меньше правой. Поэтому, делается вторая попытка. Попытки продолжаются до тех пор, пока перегрузка станет менее 3 %, а недогрузка может быть и больше, это зависит от соседних стандартных размеров профиля (например, предыдущий двутавр даёт недопустимую перегрузку, а следующий – недогрузку более 5 %). 3 задача – определение грузоподъёмности.
Здесь всё выражено, в явном виде.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.110 (0.156 с.) |
 Будем рассматривать брусья постоянного сечения, причём будем рассматривать, не только прямые, но и брусья малой кривизны. К кривым брусьям малой кривизны относятся такие брусья, у которых R / h ≥ 5, где R – радиус оси бруса, h – высота поперечного сечения бруса.
Будем рассматривать брусья постоянного сечения, причём будем рассматривать, не только прямые, но и брусья малой кривизны. К кривым брусьям малой кривизны относятся такие брусья, у которых R / h ≥ 5, где R – радиус оси бруса, h – высота поперечного сечения бруса.
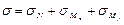 – сумма алгебраическая, так как слагаемые направлены по одной прямой (σ от кручения и сдвига нет),
– сумма алгебраическая, так как слагаемые направлены по одной прямой (σ от кручения и сдвига нет),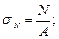
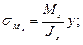 (здесь знак «+» при положительном Мх);
(здесь знак «+» при положительном Мх); 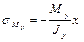 – (здесь знак «–» при положительном Му).
– (здесь знак «–» при положительном Му).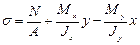
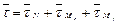 . Значения
. Значения 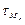 и
и 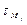 – определяются по формуле Журавского
– определяются по формуле Журавского 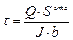 – эти касательные напряжения (от Qx и Q у) взаимно перпендикулярны;
– эти касательные напряжения (от Qx и Q у) взаимно перпендикулярны; 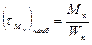 – эта формула, только для наибольших напряжений при кручении, а для любой точки – можно определить на компьютере.
– эта формула, только для наибольших напряжений при кручении, а для любой точки – можно определить на компьютере. тогда
тогда 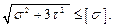 Так можно оценить прочность в любой точке бруса. Для всего бруса:
Так можно оценить прочность в любой точке бруса. Для всего бруса: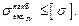


 – внутренние усилия при единичном нагружении.
– внутренние усилия при единичном нагружении.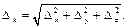
 , тогда формула Мора примет вид
, тогда формула Мора примет вид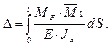

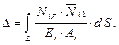
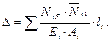

 Рама с внутренней статической неопределимостью – если за лишние неизвестные удаётся принять внутренние силы. Например, кольцо, нагруженное силами (рис. 3.5). Для нахождения внутренних сил необходимо мысленно разрезать кольцо (метод сечений), а чтобы ничего не изменилось, нужно приложить силы Х 1, Х 2 и Х 3 (которые переходят в разряд внешних), то есть рама с внутренней статической неопределимостью.
Рама с внутренней статической неопределимостью – если за лишние неизвестные удаётся принять внутренние силы. Например, кольцо, нагруженное силами (рис. 3.5). Для нахождения внутренних сил необходимо мысленно разрезать кольцо (метод сечений), а чтобы ничего не изменилось, нужно приложить силы Х 1, Х 2 и Х 3 (которые переходят в разряд внешних), то есть рама с внутренней статической неопределимостью. Далее рассмотрим вопрос об определении внутренних сил в рамах.
Далее рассмотрим вопрос об определении внутренних сил в рамах. Рассмотрим участок рамы (рис. 3.7) и любое сечение а – а. В этом сечении имеются три связи:
Рассмотрим участок рамы (рис. 3.7) и любое сечение а – а. В этом сечении имеются три связи:


 Будем рассматривать П-образную раму с защемлёнными концами (рис. 3.9). Она составлена из стержней одинаковой длины и нагружена горизонтальной силой F. Кроме силы, на раму действуют реакции в защемлениях. Неизвестные реакции можно направить как угодно – правильное направление укажет затем, знак.
Будем рассматривать П-образную раму с защемлёнными концами (рис. 3.9). Она составлена из стержней одинаковой длины и нагружена горизонтальной силой F. Кроме силы, на раму действуют реакции в защемлениях. Неизвестные реакции можно направить как угодно – правильное направление укажет затем, знак.

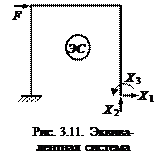 Запишем канонические уравнения метода сил, для три раза статически неопределимой системы
Запишем канонические уравнения метода сил, для три раза статически неопределимой системы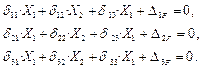
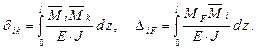
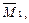
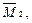
 и M F (рис. 3.12, а-г). Единичные силы и пара сил направлены так же, как и неизвестные силы Х 1, Х 2, Х 3.
и M F (рис. 3.12, а-г). Единичные силы и пара сил направлены так же, как и неизвестные силы Х 1, Х 2, Х 3.
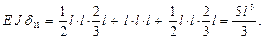
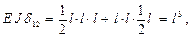
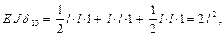
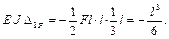
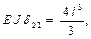
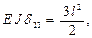
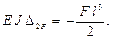
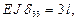
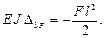
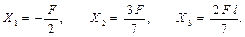
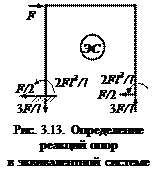 Далее нужно найти реакции опор в эквивалентной системе (рис. 3.13).
Далее нужно найти реакции опор в эквивалентной системе (рис. 3.13).
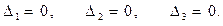


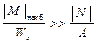 (рис. 3.16), то наиболее опасным будет сечение, где действует | М| наиб.
(рис. 3.16), то наиболее опасным будет сечение, где действует | М| наиб.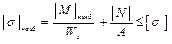

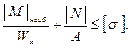
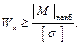



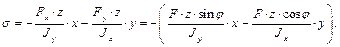
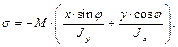

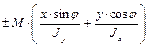 = 0, но М ≠ 0, поэтому
= 0, но М ≠ 0, поэтому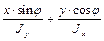 = 0 – уравнение нейтральной оси при косом изгибе.
= 0 – уравнение нейтральной оси при косом изгибе.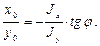
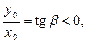 следовательно, угол β тупой.
следовательно, угол β тупой.
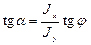

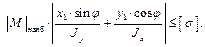
 Напомним, что эта формула справедлива только при α = const.
Напомним, что эта формула справедлива только при α = const.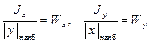 , и вынести за скобку Wx, то получим
, и вынести за скобку Wx, то получим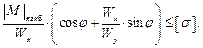

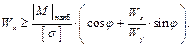

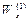 находим
находим 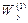 и проверяем прочность по формуле
и проверяем прочность по формуле