
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчёт на прочность цилиндрической оболочки
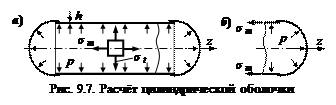
Рассмотрим для примера паровой котёл (рис. 9.7, а). Уравнение Лапласа
Для цилиндрической оболочки рт = ∞, pt = D / 2, тогда
Для определения осевых напряжений проведём сечение а – a и рассмотрим равновесие правой части цилиндра (рис. 9.7, б)
Применим третью теорию предельных напряжённых состояний
Условие прочности для цилиндрической части – Условие прочности для сферической части –
9.4 Расчёт на прочность конической оболочки, Уравнение Лапласа
Для конической оболочки (рис. 9.8, а) ρт = ∞, Рассмотрим заполненную часть оболочки
Тогда
Далее определим меридиональные напряжения (рис. 9.8, б)
Составим уравнение равновесия отсечённой части
– меридиональные напряжения заполненной части оболочки. Теперь рассмотрим незаполненную часть оболочки (рис. 9.8 в) при z ≥ H. Здесь p = 0, тогда по уравнению Лапласа Уравнение равновесия:
и откуда
Таким образом, в незаполненной части оболочки действуют только меридиональные напряжения. Построим эпюры напряжений (рис. 9.8, в) Окружные напряжения При z = 0 σ t = 0; при z ≥ H σ t = 0. Определим экстремальное значение σ t:
Меридиональные напряжения При z = 0 σ m = 0. Определим экстремальное значение σ m:
тогда наибольшие меридиональные напряжения возникают при Далее составим условие прочности конической оболочки. Оболочки, как правило, изготавливаются из пластичных материалов, поэтому применяем третью теорию предельных напряжённых состояний
σ 1 равен либо σ m, либо σ t, σ 3 = 0. Наибольшие окружные и меридиональные напряжения определяются по формулам
– условие прочности конической оболочки, наполненной жидкостью. Вопросы для самопроверки 1. Какие оболочки называются тонкостенными? 2. Какие допущения принимают в безмоментной теории оболочек? 3. Как записывается уравнение Лапласа для тонкостенных оболочек? 4. Каковы величины напряжений, возникающих в тонкостенных оболочках с внутренним давлением? 5. Как оценивается прочность сферических оболочек с внутренним давлением? 6. Как оценивается прочность цилиндрических оболочек с внутренним давлением? 7. Как оценивается прочность конических оболочек, наполненных жидкостью?
ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Мы изучали поперечный изгиб, а также продольный изгиб (устойчивость). Продольно-поперечный изгиб имеет место, если балка нагружена одновременно и продольными, и поперечными силами (вдоль и поперёк оси). Будем рассматривать прямой (плоский) продольно-поперечный изгиб, когда силы лежат в одной из главных плоскостей жёсткости балки. Пример – лонжерон летательного аппарата испытывает продольно-поперечный изгиб. 10.1. Точное решение уравнения
Пусть поперечные внешние силы приложены в плоскости наибольшей жёсткости, тогда система осей х, у и у = у (z) – прогиб в произвольном сечении. Особенность продольно-поперечного изгиба заключается в том, что здесь необходимо учитывать изгибающий момент и от продольных сил. Воспользуемся дифференциальным уравнением изогнутой оси балки. EJy " = M – уравнение, полученное при поперечном изгибе, применяется. и при продольном изгибе. В любом сечении M = M п – F · y. Первое слагаемое этого уравнения – изгибающий момент при поперечном изгибе – как его вычислить, известно. Знак минус перед вторым слагаемым, так как балка изгибается выпуклостью вверх. Подставим и преобразуем
– дифференциальное уравнение продольно-поперечного изгиба в случае, когда продольные силы вызывают сжатие. Если они вызывают растяжение, то перед k 2 нужно ставить минус.
Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общее решение этого уравнения ищем в виде y = y 0 + y *, где y 0 – общее решение однородного уравнения, y * – частное решение неоднородного уравнения.
Общее решение однородного уравнения было найдено в теме «Устойчивость сжатых стержней». Оно имело вид
Теперь найдём частное решение неоднородного уравнения. Это решение зависит от функции изгибающего момента: М п = М п(z) – есть общее решение, но мы обращаемся к частным случаям. Рассмотрим пример: балка на двух опорах, нагружена поперечной равномерно распределённой нагрузкой интенсивностью q и продольными силами F (см. рис. 10.1). Продольные силы F приложены центрально. Нам предстоит найти уравнение y *. Изгибающий момент в произвольном сечении z:
Перепишем еще раз дифференциальное уравнение
Если в правой части неоднородного дифференциального уравнения полином, то и частное решение нужно искать в виде полинома Подставим это решение в дифференциальное уравнение
Все слагаемые перенесём в левую часть и сгруппируем по степени
Как определить a, b, c? Если уравнение y * = a + b · z + c · z 2 является решением неоднородного дифференциального уравнения, то равенство нулю должно быть выполнено при любом z, в том числе и при z = 0, тогда
Теперь запишем решение:
Таким образом мы нашли частное решение, теперь запишем общее решение.
– это общее решение для рассматриваемого нагружения. Далее определим A и B из граничных условий: 1)при z = 0 y = 0 => 2)при z = l y = 0 => Отсюда
– это уравнение изогнутой оси балки, нагруженной поперечной равномерно распределённой нагрузкой интенсивностью q при продольно-поперечном изгибе. Приступаем к определению изгибающего момента. Можно это сделать по уравнению: M = M п – F · y, а можно, другим путём:
(sin k· z) ′′ = – k 2 · sin k· z, (cos k· z)′′ = k 2 cos k· z,
Можно видеть, что изгибающий момент изменяется по сложному закону. Для расчёта на прочность нужно знать наибольший момент. Как его найти? Необходимо исследовать функцию. Взять значение по границам, исследовать на экстремум – это общий подход. В данном случае просто – наибольший момент действует в среднем сечении балки. При z = l /2 Далее преобразуем (проделать самостоятельно):
Рассмотрим предельный случай, когда F стремится к нулю, тогда Если подставить в выражение (10.1), то получим неопределенность типа 0/0. Нужно применить правило Лопиталя, но можно и по другому (разложение в ряд)
и, следовательно, При k стремящемся к 0, все слагаемые, кроме первой величины – бесконечно малы. Пока k не достигнет значения 0, равенство будет приблизительным, а в пределе – это точно. М наиб = ql / 8 – это известная формула для поперечного изгиба. Особенности продольно-поперечного изгиба: 1) Обращаемся к выражению (10.1). М наиб зависит только от
2) Если (из выражения (10.1)), то М наиб → ∞ – это при возрастании F. Разберёмся в физическом смысле этого результата:
Следует обратить внимание на то, что задача получения точного решения является громоздкой, мы получили решение для частного случая. Если у балки будет несколько участков, то решение значительно усложнится. Задача громоздкая (но не сложная), поэтому применяется приближённый метод решения. 10.2. Приближённое решение уравнения Будем рассматривать случай, когда поперечные нагрузки действуют в одном направлении (рис. 10.2). В этом случае уравнение изогнутой оси балки можно представить приближённо в виде В действительности, это не совсем так, но при вычислении больших прогибов, это, почти правильно. При действии только поперечных сил: y п ≈ f п · sin (π· z / l) (при F = 0)
Подставим это, в уравнение продольно-поперечного изгиба
Разрешим выражение относительно f (самостоятельно)
Если умножить обе части уравнения на sin (π· z / l), то получим
– формула для прогиба в любом сечении балки. Это приближённая формула для определения перемещения при продольно-поперечном изгибе. Она применима только в случае, когда поперечные нагрузки действуют в одном направлении. Она оказывается, как показывает опыт, достаточно точной, при F ≤ 0, 75 F кp. Она точнее для бóльших прогибов, среди всех прогибов балки (например, для середины балки). Чем ближе к опорам, тем точность меньше. Эту формулу можно применять и для консольной балки. Получим формулу для момента
Если дважды продифференцировать выражение (10.2) по z и преобразовать, то, используя последние две формулы, получим
– эта формула работает при тех же ограничениях, что и предыдущая формула (для у). Она является достаточно точной при симметричном нагружении относительно середины пролёта. Это связано с общими свойствами приближённых функций, так как производная, увеличивает ошибки.
Для практики, этот случай не представляет интереса, а расчёт ведут только по поперечным силам (растяжение может быть учтено через σ = F / A). Посмотрим, насколько точна приближённая формула для M. Вычислим изгибающий момент для балки (рис. 10.3), которую рассчитаем по точной и приближённой формулам. Точное решение.
Подставим условия:
Приближённое решение.
Видно, что расхождение результатов составляет менее одного процента. 10.3. Расчёт на прочность Вспомним условие прочности при поперечном изгибе, когда нет продольных внешних сил
Эта формула выведена в предположении, что при увеличении внешних сил в n раз, внутренние силы увеличатся тоже в n раз. При продольно-поперечном изгибе эту формулу применять нельзя в силу нелинейности задачи. Эта нелинейность приводит к тому, что увеличение внешних нагрузок в п раз вызывает увеличение напряжений в бóльшее число раз. В справедливости этого вывода можно убедиться, рассматривая приближённую формулу (10.3) для изгибающего момента Выведем новую формулу. Будем считать, что при переходе к предельному состоянию внешние нагрузки возрастают пропорционально. В таком случае коэффициент запаса п т можно представить:
– здесь F т и F т = п т· F, Запишем формулу для напряжений при продольно-поперечном изгибе
Первое слагаемое (F / A) приходится учитывать, так как порядок напряжений одинаков. Вместо σ наиб подставим σ т.
Разделим обе части на п т
– это равенство можно рассматривать как условие полного использования грузоподъемности балки, тогда
– условие прочности при продольно-поперечном изгибе (то есть для сжато-изогнутых балок). Нелинейность этой формулы проявляется через коэффициент п т в знаменателе. За счёт нелинейности увеличивается левая часть условия прочности, а это означает, что допустимые нагрузки. будут несколько меньше. Может быть, случай растянуто-изогнутых балок, но с практической точки зрения, это менее интересная задача и продольная сила F не учитывается или учитывается через F / A.
Вопросы для самопроверки 1. Когда брус испытывает продольно-поперечный изгиб? 2. Как записывается дифференциальное уравнение продольно-поперечного изгиба? 3. Какой вид имеет точное решение дифференциального уравнения продольно-поперечного изгиба? 4. Как определяются перемещения при приближённом решении дифференциального уравнения продольно-поперечного изгиба? 5. Как оценивается прочность стержней при продольно-поперечном изгибе? 11. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ К наукам, изучающим прочность элементов конструкций, кроме сопротивления материалов относятся теория упругости, теории пластичности и ползучести, строительная механика и материаловедение. Содержание перечисленных дисциплин: Сопротивление материалов В сопротивлении материалов изучается действие сил на тело, которое можно считать брусом (стержнем). Брус – это тело, один из размеров (длина) которого значительно больше двух других размеров (размеров поперечного сечения). Задачи для толстостенных цилиндров, тонкостенных оболочек, которые мы изучали, не относятся к сопротивлению материалов – это задачи теории упругости. Таким образом, в сопротивлении материалов изучаются все стороны и особенности сопротивления брусьев (простые сопротивления и сложные сопротивления). Ещё, что очень важно, задача сопротивления бруса внешним силам решается с использованием гипотезы плоских сечений. Гипотеза плоских сечений заменяет уравнения совместности деформаций и имеет приемлемую точность, только для брусьев. Для тел, которые нельзя считать брусьями, гипотеза плоских сечений, приводит к большим ошибкам. Следовательно, в сопротивлении материалов изучается действие сил на брусья и при решении используется гипотеза плоских сечений. Теория упругости В теории упругости изучается действие сил на тело произвольной формы. Задача решается на основании точных уравнений, выражающих закономерности деформации системы. В теории упругости рассматриваются также, и брусья (действие сил на брус), но вместо гипотезы плоских сечений, используются точные уравнения совместности деформаций. Математический аппарат теории упругости сложнее, чем в сопротивлении материалов, так как постановка задачи, является более полной. В сопротивлении материалов используются обыкновенные дифференциальные уравнения, причём сравнительно простые, а в теории упругости – системы дифференциальных уравнений в частных производных, к тому же, не во всех случаях, известно решение этой системы. В теории упругости существуют два направления: математическое и прикладное. Поэтому существуют математическая теория упругости и прикладная теория упругости. В математической теории упругости исходят из точных дифференциальных уравнений, выражающих закономерности деформации тела. В прикладной теории упругости применяют деформационные гипотезы, то есть, вместо точных уравнений, отражающих закономерности деформации системы, для решения применяют, приближённые соотношения, что позволяет упростить задачу в математическом отношении. Следует заметить, что речь идёт о разумных гипотезах, которые, затем проверяются экспериментально. Далеко не для всех тел, можно применять эти гипотезы. Одной из задач прикладной теории упругости, является задача об изгибе пластинок. Для решения этой задачи, применяется гипотеза неизменности нормали к срединной поверхности пластины. Задача намного упрощается в математическом отношении, а решение, оказывается достаточно точным. Таким образом, сопротивление материалов, можно считать одной из простейших задач прикладной теории упругости. Основные уравнения теории упругости и пример их применения Рассмотрим произвольное тело, нагруженное самоуравновешенной системой внешних сил (рис. 11.1). Напряжения в любой точке упругого тела: σх = σх (x, y, z), Отыскание этих функций является задачей теория упругости. Без вывода, запишем уравнения, которым должны удовлетворять напряжения.
 (11.1) (11.1)
– уравнения статики в случае отсутствия объёмных сил (уравнения равновесия).
– уравнения совместности деформаций. Здесь σ = σ x + σ y + σ z. Должны быть также удовлетворены уравнения равновесия на контуре тела, так называемые контурные условия (рис. 11.2):
Компоненты напряжённого состояния должны удовлетворять уравнениям (10.1), (10.2), (10.3). Доказывается, что эти системы уравнений имеют единственное решение. Решаются эти уравнения, строго говоря, методом отгадывания. Пример. Для стержня, нагруженного по торцам равномерно распределённой нагрузкой, предлагается следующее решение (рис. 11.3) σ x = σу = 0, σ z = σ, τ xy = τу z = τ zx = 0.
а) уравнения статики – удовлетворяются; б) уравнения совместности деформаций σ x + σу + σ z = σ = const – удовлетворяются; б) контурные условия нужно рассмотреть всю поверхность. На боковой поверхности На верхнем и нижнем торцах Следовательно, предложенное решение является точным. Если на торцах. иное распределение σ z, например, приложены сосредоточенные силы, то, строго говоря, предложенное решение неприменимо, так как не удовлетворяется. третье уравнение системы (10.3). Однако предложенное решение, всё же можно применить, используя принцип Сен-Венана. Для этого, сосредоточенные силы заменяем равномерно распределёнными силами, статически им эквивалентными, то есть σ = F / A. В результате такой замены. изменяется напряжённое состояние. только вблизи от торца (на глубину одного размера сечения). В остальных точках бруса. предложенное решение применимо. Следовательно, оно применимо. и к нагружению сосредоточенными силами, но в области, исключающей торцы.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.254.122 (0.204 с.) |

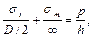 отсюда
отсюда
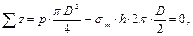 отсюда
отсюда 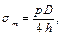 σ r ≈ 0, следовательно,
σ r ≈ 0, следовательно, 
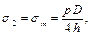 σ 3 = σ r = 0,
σ 3 = σ r = 0,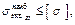 где
где 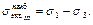
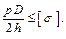
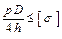 , то есть наиболее нагруженной является цилиндрическая часть и условие прочности для всего цилиндра, будет иметь вид
, то есть наиболее нагруженной является цилиндрическая часть и условие прочности для всего цилиндра, будет иметь вид
 где ρ – плотность жидкости.
где ρ – плотность жидкости.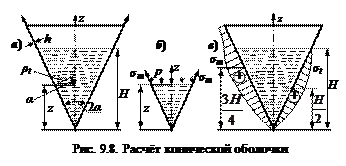
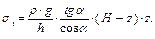


 окончательно
окончательно
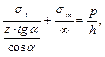 отсюда σ t = 0.
отсюда σ t = 0.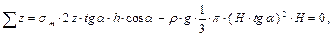
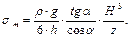
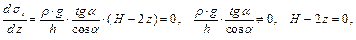 тогда наибольшие окружные напряжения возникают при z = H / 2.
тогда наибольшие окружные напряжения возникают при z = H / 2.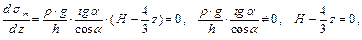
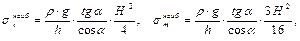 следовательно,
следовательно, 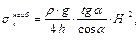 то есть самая опасная точка конической оболочки находится в середине заполненной части и это условие
то есть самая опасная точка конической оболочки находится в середине заполненной части и это условие Рассмотрим расчётную схему продольно-поперечного изгиба – балка на двух опорах, нагружена поперечной равномерно распределённой нагрузкой интенсивностью q и продольными силами F (рис. 10.1). Продольные силы приложены центрально. Если силы приложены внецентренно, то их нужно переместить к центру и возникает дополнительная пара сил F · e, где e – эксцентриситет силы.
Рассмотрим расчётную схему продольно-поперечного изгиба – балка на двух опорах, нагружена поперечной равномерно распределённой нагрузкой интенсивностью q и продольными силами F (рис. 10.1). Продольные силы приложены центрально. Если силы приложены внецентренно, то их нужно переместить к центру и возникает дополнительная пара сил F · e, где e – эксцентриситет силы. – положительная величина, тогда
– положительная величина, тогда
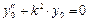 – решение однородного уравнения.
– решение однородного уравнения. "
" 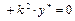 – решение неоднородного уравнения.
– решение неоднородного уравнения.
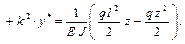

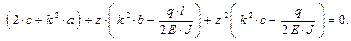
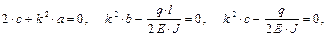 поэтому
поэтому


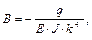
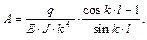

 так как
так как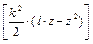 ′′ = – k 2
′′ = – k 2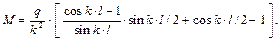
 (10.1)
(10.1)

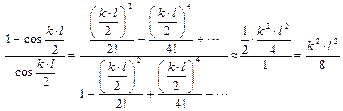
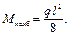
 (в формуле sin и cos), то есть, связь между внутренними и внешними силами не линейная или иначе, между внешними силами и напряжениями – нелинейная, и, следовательно, связь между прогибами и внешними силами, тоже нелинейная. Это единственная нелинейная задача в сопротивлении материалов. Следовательно, принцип сложения внешних сил (принцип суперпозиции) неприменим.
(в формуле sin и cos), то есть, связь между внутренними и внешними силами не линейная или иначе, между внешними силами и напряжениями – нелинейная, и, следовательно, связь между прогибами и внешними силами, тоже нелинейная. Это единственная нелинейная задача в сопротивлении материалов. Следовательно, принцип сложения внешних сил (принцип суперпозиции) неприменим.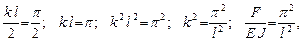 отсюда
отсюда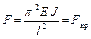 – при таком значении продольные силы, изгибающий момент обращаются в бесконечность, следовательно, наблюдается явление, происходящее тогда, когда F = F кр – то есть происходит потеря устойчивости.
– при таком значении продольные силы, изгибающий момент обращаются в бесконечность, следовательно, наблюдается явление, происходящее тогда, когда F = F кр – то есть происходит потеря устойчивости. Теперь обращаемся к диффе-ренциальному уравнению продольно-поперечного изгиба M = M п – F · y. Вычислим каждое слагаемое
Теперь обращаемся к диффе-ренциальному уравнению продольно-поперечного изгиба M = M п – F · y. Вычислим каждое слагаемое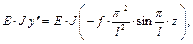
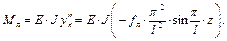

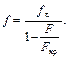
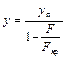 (10.2)
(10.2)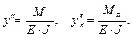
 (10.3)
(10.3) Если силы F вызывают растяжение, то в этом случае, в дифференциальном уравнении будет + F · y, а общее решение однородного уравнения выразится через гиперболические функции, и в приближенных формулах, в знаменателе, второе слагаемое будет со знаком «+», то есть
Если силы F вызывают растяжение, то в этом случае, в дифференциальном уравнении будет + F · y, а общее решение однородного уравнения выразится через гиперболические функции, и в приближенных формулах, в знаменателе, второе слагаемое будет со знаком «+», то есть 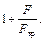
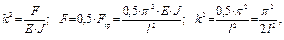 тогда
тогда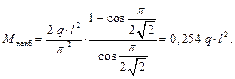
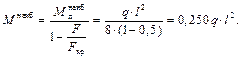
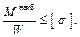
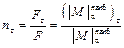
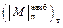 – это нагрузки, при которых наибольшее напряжение в балке достигает σ т. По способу допускаемых напряжений – это опасные нагрузки.
– это нагрузки, при которых наибольшее напряжение в балке достигает σ т. По способу допускаемых напряжений – это опасные нагрузки. – это нам будет необходимо.
– это нам будет необходимо.
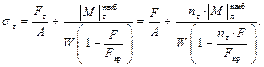
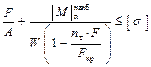

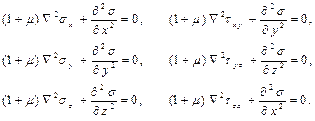 (11.2)
(11.2)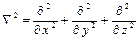 – оператор Лапласа второго порядка,
– оператор Лапласа второго порядка,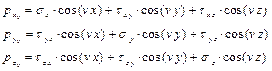 (10.3)
(10.3)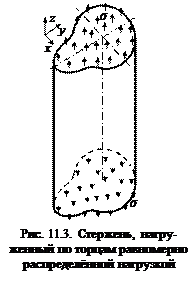 Проверим, удовлетворяет ли это решение, уравнениям теории упругости:
Проверим, удовлетворяет ли это решение, уравнениям теории упругости: – удовлетворяются;
– удовлетворяются; .
. 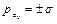 , третье уравнение системы (10.3)
, третье уравнение системы (10.3)  , то есть тоже удовлетворяется.
, то есть тоже удовлетворяется.


