Особенности древней преднауки.

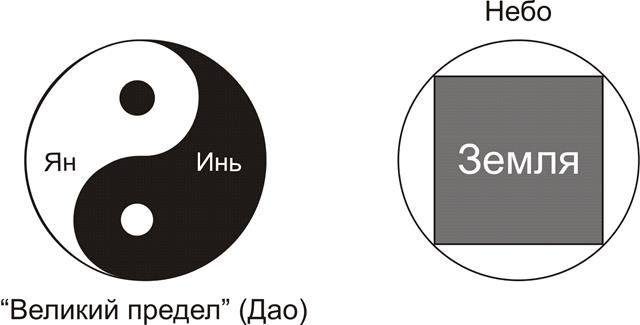
Познание ради хозяйственной практики. Встав на путь культуры, человечество быстро прогрессировало. К IV-II тысячелетиям до н.э. в Египте, Китае, Индии, Вавилоне сложились древние, относительно зрелые цивилизации. Хозяйственная практика в них достигла значительных высот. В Египте и Вавилоне развилось сложное строительное искусство: глинобитные строения из сырцового кирпича, храмы и пирамиды из каменных блоков в несколько тонн. Существовала металлургия меди и бронзы, из растений получали различные красители. Для измерения продуктов использовали механические весы. В 1936 г. недалеко от Багдада был найден медный кувшин (I в. до н.э.), бывший корпусом аккумуляторной батареи. При наполнении его какой-либо кислотой (уксусной, лимонной) в качестве электролита кувшин в течение 18 дней вырабатывал электрический ток напряжением в 0,5 вольта. Последовательный ряд таких элементов мог обеспечить гальванизацию металлов.

В Египте высокого развития достигли анатомия и медицина в связи с практикой мумифицирования. Готовились врачи разных специальностей, они знали систему кровообращения, выделяли роль мозга как управляющего центра тела (паралич ног объяснялся повреждением мозга). Хирурги делали трепанацию черепа. Пломбирование зубов было весьма широкой практикой. Сохранившиеся врачебные рецепты говорят о том, что врачи и аптекари неплохо знали азы химии лекарств. В «домах жизни» (египетские больницы) составляли описания признаков многих болезней. При раскопках гробниц найден богатый набор хирургических инструментов.

Трудовая и социальная практика встречалась с такими «вызовами», которые не могли не стимулировать развитие познания. Если взять сельское хозяйство Древнего Египта, то оно всецело определялось рекой Нил. Вдоль ее участки земли принадлежали разным сельским общинам. Разливы Нила регулярно стирали границы участков речным илом, и их восстановление стало важной практической задачей. Государственные чиновники были вынуждены изображать очертания участков точными чертежами на папирусе. И уже по ним восстанавливали границы, пользуясь туго натянутой веревкой с мерными узлами. При разметке исходных границ надо было вычислять площади участков, имеющих самую различную форму (треугольник, квадрат, параллелограмм и т.п.). В этих условиях возникла практическая геометрия, где пространственные представления сформированы измерениями.

Познание ради религиозных идеалов. При проведении раскопок в Анатолии (Турция) археологи в 2005 г. обнаружили остатки храмового комплекса, созданного за 10 тысяч лет до н.э. Люди каменного века создавали каменные строения для поклонения богам. На колоннах храма найдены строчки знаков. Стало быть, люди раннего неолита уже умели записывать свои священные формулы [1, с. 78]. Исчезнувшая цивилизация майя оставила на территории современной Панамы огромные каменные шары весом до 15 тонн, выполненные с удивительной геометрической точностью. Наиболее правдоподобное объяснение – шар обозначал место захоронения жреца-вождя.

Подчиненность древнего познания мифо-религиозному мировоззрению очевидна. Архаичные верования пронизывали все и вся, даже изобретение техники подчинялось этому влиянию. Так, колесо было посвящено богам. В буддистских храмах Тибета и Японии вместе с молитвенными колесами (символ «мандалы») находятся ветряные и водяные колеса. Индусы изобрели бурав с огнем для возжигания священного огня в жертвоприношениях. Это устройство весьма эффективно и способно получать огонь до 360 раз в сутки.

Главная фигура преднауки – жрец. В Вавилоне, Индии и Египте жречество есть узкое и привилегированное сословие людей (каста). Этот статус наследуется, т.е. переходит от старшего поколения младшему посредством особого закрытого обучения. (В Египте сохранились записи 365 поколений жрецов). Жрецы владели и поддерживали тайное знание, они не могли о нем сообщить непосвященным. Сохранилась жреческая заповедь: «все для народа, но через народ – ничто». Если вавилонские жрецы занимались астрономией для целей религиозного культа (жертвоприношения, гадательные гороскопы и т.п.), то профанам давалась облегченная версия: «небесные светила суть лики богов, наблюдающих за земной жизнью». В таком контексте религия снимала с повестки дня тему объяснения. Вопрос «почему так?» бессмыслен, ибо сотворенное богами надо принимать на веру. Да, и жрецы занимались тем, что добросовестно фиксировали божественный порядок.

Обязательным элементом религиозного культа была музыка и песнопение. Молитвам и священным гимнам придавался упорядоченный ритм, который и становился священной музыкой. Ее структурный лад выражался числовыми соотношениями, изучение которых естественно переходило в математическое исследование. Этот путь прошли греческие пифагорейцы, индийские математики и китайские мудрецы. Последние смогли перенести учение о музыкальных тонах даже на медицину.

Китайская преднаука осуществлялась государственными чиновниками. Древний Китай был земледельческой цивилизацией с развитым ремеслом. До II в. до н.э. в политическом плане он представлял собой конгломерат отдельных царств (княжеств). В каждой из них ключевой управляющей группой были государственные чиновники. Претенденты на чиновную должность испытывались на конкурсных экзаменах. Самой почитаемой должностью считался администратор по гидротехнике. Провалившиеся на имперских экзаменах шли в военные (в Индии, Вавилоне, Египте военачальники были по социальному положению выше хозяйственных управленцев).

Китайское государство всемерно поддерживало преднауку. С начала II тысячелетия до н.э. особая группа чиновников занималась астрономией и астрологией. В одном из царств с 840 г. до н.э. таким «исследователям» запрещалось общаться с другими чиновниками и простолюдинами, чтобы не происходила утечка ценных сведений. Кроме этого, государство вело субсидирование ряда исследовательских экспедиций: а) геодезическое исследование дуги меридиана от Индокитая до Монголии (VIII в.); б) экспедиция для нанесения на карту неба созвездий Южного полушария. Государство также давало задания на разработку объемных энциклопедий (медицинских, сельскохозяйственных и др.) и издавало их.

Государственная поддержка преднауки была обусловлена получением ее практических приложений. Уровень технических изобретений был для своего времени высоким. К началу нашей эры были сконструированы механические двигатели, использующие силу падающей воды и водоподъемный насос. Достижением мирового значения стало изобретением компаса в виде квадратной железной пластины со свободно вращающейся на ее поверхности магнитной «ложкой», ручка которой указывала на юг. Чжан Хэн (78 - 139) сконструировал первый прототип сейсмографа.

Древнекитайская гадательная математика и астрономия. Графическая фиксация количества появилась очень рано. Уже 30 тыс. лет назад кроманьонец использовал лучевые кости волка и группировал зарубки пятерками. Но принцип «один объект – один знак» примитивен и многие тысячи лет ушли на изобретение плодотворной системы счета. Решение было найдено не за счет умножения знаков, а на пути их системной связи. Параллельно этому поиску шло совершенствование знаков для представления объектов и их множеств. Открытие числовых систем было вызвано социальными причинами. Расцвет ранних городов вызвал экономические отношения обмена, торговли, займов и долгов. В хранилищах скапливались большие количества зерна, овощей, масел, что требовало должного учета. У наемных работников надо было учитывать множество рабочих дней. Требовались также предсказания не только природных циклов для аграриев, но и возможных войн для политиков. На вызовы времени этнические культуры давали разные ответы.

В Древнем Китае счетная практика началась с записей-зарубок на бамбуковых планках, затем перешли на узелковое письмо. Оно в дальнейшем уступило место триграммам и гексаграммам, а также иероглифам. Считается, что данный процесс возник в практике гаданий династии Инь (предсказание погоды, урожая, войны и т.п.). Мнения расходятся лишь в отношении способов гадания. Фэн Ю-лань полагал, что гадание происходило на панцирях черепах. На панцирь наносился текст вопроса, затем он прокалывался металлическим раскаленным копьем, и получавшиеся трещины истолковывались как ответ. Сплошная линия (ян) и линия с прерывом (инь) стали геометрическими знаками, которые заменили пророческие трещины и стали основой двоичного исчисления (оценка Г. Лейбница). Ван Юй-шен взял за основу практику гаданий на стеблях тысячелистника. Черта ян стала символом нечетных чисел (1, 7, 9), а черта инь – знаком четных (6, 8). Комбинирование черт в триграмму и гексаграмму позволило гадательные приемы преобразовать в математические операции с числами и геометрическими фигурами. Так возникла система «чжоуи» с ведущим приемом гематрии, где связь иероглифов превращается в комбинацию чисел и наоборот. Перемены имеют Великий Предел. Один [дао] рождает двоицу [инь и ян], она рождает четыре символа, а они – восемь триграмм, а все это – 64 гексаграмм. «Такое количество схем, способное отразить тьму вещей», и фигурирует в «Книге Перемен». Шестеричность китайской нумерологии обусловлена необходимостью получить 64 гексаграмма и 384 черты. Последнее число есть максимальное число дней в лунном календаре (6 месяцев – 29 дней, 6 месяцев – 30 дней, 1 месяц – 30 дней). По сути дела древние китайцы изобрели счетную машину, где алгоритм указывает, как выстраивать числовой ряд: 1, 2, 4, 8, 16, 32, 64. Линейная последовательность здесь выводится из пространственной структуры [2, с. 20-25]. Стрелки указывают порядок считывания триграмм внутри их пар; цифры – последовательность самих пар. (При всей наивности такой математики древние китайцы уже во II тысячелетии до н.э. считали до 30 тысяч, вычисляли десятичные дроби, они первыми изобрели отрицательные числа и владели весьма точным значением числа π).

Китайская нумерология приобрела астрономический и натурфилософский характер. Прежде всего, все планеты и важные созвездия (Зодиак) были обозначены гексаграммами. Так, гексаграмма Цянь стала знаком Юпитера, Сюй символизирует Венеру. «Великий Предел» обозначил годичный цикл уменьшения и роста сил ян и инь, эта двоица выразила летнее и зимнее солнцестояние. Единство земли (пространства) и неба (времени) предстало в особой комбинации цифровых и геометрических символов: Земля – 8 и квадрат, Небо – 12 и круг. Площадь квадрата – 8 единиц, площадь круга – 12.

Позиционный принцип вавилонской математики. Его сконструировали через две тысячи лет после введения алфавитного представления знаков языка. Важной предпосылкой здесь стал выбор основания для группировки чисел. Основанием может быть любое число, большее единицы, но большинство народов выбрало: 5, 10, 20 (число пальцев на руках и ногах). У кельтских племен и индейцев Майя сложилась 20-ричная система, у индусов, греков и славян числа группировались по десять. Десятиричная система без позиционного принципа была в Древнем Египте. Здесь каждой группе чисел, кратной десяти, присваивали свой иероглиф:

 

 

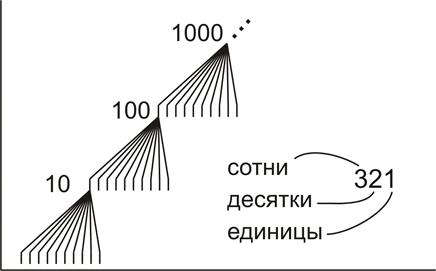
Основными вычислительными операциями были сложение и умножение, обратимость операций сложение / вычитание, умножение / деление не осознавалась. Позиционный принцип построения чисел был открыт шумерами или вавилонянами (Месопотамская цивилизация). Сначала шумеры разработали десятиричную систему и открыли ценнейшую идею. При увеличивающейся мощности множеств числовые знаки можно организовать в иерархию: вместо группы, кратной десяти, вводится новый знак, который используется как единица следующего разряда. И такой переход позволяет составить бесконечную последовательность.

 

 

В начале III тысячелетия до н.э. вавилоняне перешли на шестидесятиричную систему счисления. Ее возникновение связано с астрономией, данное основание облегчило запись наблюдений за небом, измерения времени стало естественным в лунном календаре (не случайно и современная цивилизация принимает 60 сек. в 1 минуту, 60 мин. в 1 час, 24 часа – это 1/5 от 60). Для измерения площадей и объемов надо было освоить операцию деления. А она дает отношение чисел или дроби, для их вычисления были созданы таблицы отношений: 1(60):20=3; 1:9=6,40; 1:24=2,30. Все четыре арифметических действия выполняются здесь по единым алгоритмическим правилам. Вавилонские математики создали числовую алгебру с решениями линейных, квадратных, биквадратных и кубических уравнений. Также решались системы линейных уравнений с двумя неизвестными, хотя из доантичных форм вавилонская математика оказалась одной из самых развитых, у нее были свои недостатки. Прежде всего, отсутствовал специальный знак пустого места, или нуль. Это создавало большие трудности. Допустим, что наше число превышает три сотни на две единицы. С нулем записать его легко - 302, а без нуля нужны сложные ухищрения. Кроме того, идея божественного происхождения целых чисел привела к догматическим неточностям. Год свелся к 360 (60∙60) дням и неучтенными оказались 5 дней. В математике по этой причине вне признания остались дроби и иррациональные числа [3].

Математический нуль изобретен под влиянием философии. Нуль изобрели древнеиндийские математики. Данное открытие было обусловлено философской позицией. Буддийский философ Нагарджуна (II в. н.э.) разработал учение о пустоте («шунья»), согласно которому пустота как отсутствие вещей есть изначальная сущность бытия. Все материальные образования возникли из мировой пустоты. (Здесь имеется явная перекличка с даосизмом, где пустотное дао порождает через ян и инь, ци и дэ «тьму вещей»). Онтологический образ пустоты стал необходимой предпосылкой перехода к математической абстракции – «нулю». Такое нововведение не было случайностью и в математическом отношении. Древнеиндийская математика достигла высокого уровня развития. Здесь была разработана десятиричная позиционная система исчисления. Индийские обозначения чисел и арифметические правила через арабов пришли в Европу и легли в основу современной арифметики. Свои достижения были в алгебре и они уже связаны с персоналиями. Так, Арьябхата (V - VI вв.) предложил оригинальное решение линейного уравнения, близкое к современному. Он же дал одно из относительно точных значений числа π. Многие современные математические термины – «цифра», «корень», «синус» и т.п. – имеют индийское происхождение.

Практика и религия породили астрономию. У М. Мамардашвили есть интересное объяснение происхождения астрономии. Древние люди непрерывно испытывали сильные нервно-психические потрясения или стрессы. Психологических техник еще не было. И вот наши предки открыли первую из них – регулярные наблюдения неба. Эта реальность демонстрировала людям высокий порядок и устойчивость, такое состояние не могло не внести в расстроенные души лад и гармонию. Данное соображение имеет свою убедительную силу и все же, как психологическое, оно должно отдать приоритет более важным факторам – практике и мировоззрению.

Существуют научные свидетельства очень раннего возникновения первых элементов астрономии. Уже в верхнем палеолите (около 30 лет до н.э.) человек придумал нотацию (запись) для лунных циклов. 15 тысяч лет назад возник интерес к годичному пути Солнца через созвездия. Были установлены «верхние», «средние» и «нижние» созвездия, в которых Солнце находится в весенне-летнее и осенне-зимнее время. Это дало возможность сформировать представление о такой небесной регулярности как «Зодиак» [4, с. 31-36]. За всеми этими новациями стояли потребности мифорелигиозной и хозяйственной практики.

Если взять китайскую культуру, то астрономия здесь была вписана в предсказательную технику, частным аспектами которой были прогноз погоды для растениеводства и предвидение важных социально-политических событий (войн, эпидемий и т.п.) С VI в. до н.э. китайские астрономы организовали регулярные наблюдения за небом. Властные структуры задали им жесткую установку – фиксировать все значимые перемены на небе и учитывать их в гаданиях. Санкции за нарушения были строгие. Если случалась какая-то непредсказуемая напасть, придворных астрономов казнили. Вот почему в китайских анналах отмечено более 50 новых или «временных» звезд (вспышки «сверхновых» звезд), что европейские астрономы стали фиксировать только в Новое время. Ган Дэ и Ги Шен составили звездный каталог, Чжан Хэн сконструировал небесный глобус, описав 2500 звезд и включив их в 320 созвездий. Китайские астрономы научились точно вычислять лунные и солнечные затмения. В 28 г. до н.э. признано существование пятен на Солнце.

Свои достижения имела египетская астрономия. Она была ориентирована на предсказание разливов Нила. Для этого был создан солнечный календарь, где год делился на три сезона по четыре месяца, 30-дневный месяц делился на три декады. Наблюдения показали, что разлив Нила сопряжен с появлением после долгого перерыва на рассвете первого нового года звезды Сириус. Поскольку не учитывался високосный год, утренний восход Сириуса расходился с новым годом на один день. Через 120 лет эта ошибка была уже ощутимой. И все же лунные и планетные таблицы египтян давали точные предсказания.

Египетская астрономия была пронизана религиозным духом. Солнце, Луна, планеты и выделенные звезды представлялись как небесные символы жизни богов. На гробнице Сета есть такая запись: «деканы (восходящие над восточным горизонтом через каждые десять дней звезды) умирают один за другим и затем очищаются в доме бальзамирования в преисподней, чтобы возродиться после 10 дней невидимости». Если в Древней Индии астрономических обсерваторий не было вообще, то у народов майя к концу I тыс. н.э. было построено 18 обсерваторий. Каждая из них представляла одновременно храм пирамидальной формы, стороны были строго ориентированы по сторонам света. Жрецы с высокой точностью устанавливали точку восхода Солнца в периоды солнцестояния и равноденствия [5, с. 149].

Знание в виде рецептурных правил. Ориентация преднауки на религиозную и хозяйственную практику наложила на нее особую печать. Все основные и общие результаты познания приобретали прикладной характер, т.е. они становились правилами интеллектуальных действий по решению задач. В египетском папирусе Ринда, вавилонских глиняных текстах сохранились конкретные примеры практических задач и соответствующих правил. Речь идет о специальной письменности, посредством которой осуществлялось обучение чиновников-писцов. Цель всех задач сводилась к нахождению численных решений, удовлетворяющих внешним практическим условиям, которые в каждой задаче варьируются: а) условия наследования; б) нормы оплаты труда; в) предпосылки для вычисления площади, объема и т.п. Типичная задача несла сведения о типичных условиях, и нужно было найти некий значимый для практики параметр. К примеру, сколько требуется весовых единиц (мер) ячменя, чтобы приготовить 20 единиц объема пива? При обучении будущим писцам давали правила расчета и конкретные образцы решения типичной задачи. Освоив такие примеры, писцы ничего нового в будущем не могли создавать. Их делом были расчеты по унаследованным формулам, где менялись лишь фактические данные, правила же оставались неизменными.

Важно отметить приближенный характер расчетов. Хотя правила давали общие предписания для вычислительных операций, для их эффективного действия были нужны специфические численные коэффициенты. Они и создавали нужное приближение к учету конкретики. Так, у вавилонян был весьма значителен массив коэффициентов для: а) среднего кирпича (объем и вес); б) стены (площадь); в) меда (вес); г) ячменя; д) типичного грузового судна (объем); е) тростника и т.п. Основные коэффициенты были сведены в таблицы, но очень многие надо было запоминать [6, с. 56-59].

Итак, древняя преднаука была исключительно эмпирической и ориентировалась на приблизительные расчеты. Идеал строгой точности возникнет только в античной Греции и он породит теоретическую науку. И все же не надо недооценивать преднауку. Ее субъективные правила, приблизительные правила и коэффициенты стали тем необходимым «жизненным миром» (Э. Гуссерль), логическая обработка которого и дала научную теорию. Без богатого практического опыта стройное здание теории появиться бы не могло. Кроме того, не надо забывать и о том, что все великие достижения древних цивилизаций возникли на основе преднаучных знаний: пирамиды, зиккураты, астрономия, сложная хозяйственная жизнь. Примером для подтверждения может быть строительство водопровода на греческом острове Самос (родине Пифагора). С двух сторон горы Кастро одновременно стали пробивать два туннеля. В середине горы каналы не совпали всего лишь на 5 метров по высоте и на 2 метра по горизонтали. Такой точности могут позавидовать и современные специалисты по подземным коммуникациям. Водопровод был построен в 530 г. до н.э.