
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что доказал опыт Штерна и Герлаха?Содержание книги
Поиск на нашем сайте Принято считать, что основополагающим экспериментом, доказавшим наличие собственных магнитных моментов у атомарных электронов, является опыт Штерна и Герлаха [Ш1]. Они, в откачанном объёме, направляли слабый ленточный пучок атомов серебра (с одним внешним электроном) сквозь зазор электромагнита, вдоль острия одного из его полюсов. На нейтральные атомы магнитное поле не действует, но если атом имеет собственный магнитный момент, то в неоднородном магнитном поле, создававшемся благодаря особой форме наконечников полюсов электромагнита, на атом должна действовать ненулевая сила. Согласно представлениям квантовой механики, в опыте Штерна-Герлаха магнитный момент атома серебра мог быть ориентирован либо по внешнему магнитному полю и, значит, по его градиенту, либо против внешнего магнитного поля и, значит, против его градиента. Поэтому ожидалось, что, при пролёте вдоль острия полюса, одна часть атомов отклонится в направлении к острию, а другая – в направлении от острия. Сразу за окончанием острия находилась стеклянная пластинка, на которой осаждались пролетевшие вдоль острия атомы серебра, и картина их осаждения исследовалась с помощью измерительного микроскопа. Штерн и Герлах в своих статьях [Ш2,Ш1] заявляли о том, что они получили не подлежащее никаким сомнениям доказательство «пространственного квантования в магнитном поле», из которого следует наличие у атома серебра магнитного момента в один магнетон Бора. Но обратим внимание на главную методологическую ошибку, которой они обеспечили приговор своему результату. Опыт считался ключевым в вопросе о пространственном квантовании магнитных моментов: если обнаружилось бы расщепление атомного пучка, то подтвердились бы представления квантовой механики. И расщепление обнаружилось, но почему-то была проигнорирована важная тонкость: для подтверждения квантовой механики было необходимо, чтобы все атомы серебра, влетавшие в магнитный зазор, имели одну и ту же скорость. Ведь если бы атом отклоняла постоянная сила, пропорциональная градиенту магнитного поля и не зависящая от скорости атома, то результирующее линейное отклонение d z атома зависело бы от времени t действия этой силы – а это время равно отношению длины l области неоднородного поля к скорости атома V. То есть, линейное отклонение, набранное атомом, зависело бы от его скорости – и весьма критично: при постоянном поперечном ускорении a оно составляло бы d z = a t2/2=(a /2)(l 2/ V 2), т.е. оно было бы обратно пропорционально квадрату скорости атома. Теперь заметим, что исходный пучок атомов серебра выходил из отверстия в стенке печи, содержавшей в своей полости пары серебра. Для температуры 1050оС [Ш1], максвелловское распределение атомов серебра по скоростям имеет пик при скорости 470 м/с и ширину на полувысоте около 500 м/с. Но, в опыте Штерна-Герлаха, никакая селекция атомов пучка по скоростям не проводилась. Значит, в магнитном зазоре пролетали атомы, имевшие разброс по скоростям ~100% – что, по логике действия неоднородного поля на магнитные моменты атомов, дало бы разброс линейных отклонений ~200%. Тогда не наблюдалось бы расщепление пучка: отпечаток представлял бы собой размытое сплошное пятно, и ни о каком определении магнитного момента атома серебра, «равного одному магнетону Бора», с точностью в 10% [Ш1], не могло бы быть и речи. Однако, расщепление пучка имело место. Правда, исходный ленточный пучок оставил «самый удачный» отпечаток не в виде двух полосок – которые дали бы атомы, отклонившиеся в полёте либо к острию, либо от острия – а в виде своеобразной замкнутой фигуры (см. Рис.7.8) [Ш1]. Эта «улыбка Чеширского кота» наводит на подозрение: а не
Рис.7.8. Отклонение «вверх» на отпечатке соответствует отклонению в направлении к острию.
получилась ли она в результате классического, электромагнитного воздействия на летящие атомы? Нам, конечно, напомнят, что электромагнитным воздействиям подвержены заряженные частицы, а не нейтральные атомы. А мы в ответ тоже напомним, что, по логике «цифрового» физического мира, «нейтральный» атом способен имитировать ненулевой электрический заряд в диапазоне от - e до + e – через продуцирование зарядовых разбалансов (7.1). Как обсуждалось выше (7.7), в магнитном поле атомы металлов продуцируют кратковременные «щелчки» зарядовых разбалансов чередующихся знаков – с частотой, прямо пропорциональной индукции магнитного поля. Обладая, на коротких интервалах времени, эффективным зарядом - e или + e, летящий атом серебра подвержен электромагнитным воздействиям, искривляющим его траекторию. И, как показал наш анализ опыта Штерна-Герлаха, магнитное воздействие не приводило здесь к заметным траектория атомов – магнитное поле обеспечивало лишь «щелчки» зарядовых разбалансов, а результирующая картина рассеяния определялась электрическими воздействиями на атомы при их пролёте сквозь малые диафрагмы. Действительно, в нескольких миллиметрах от входного торца зазора магнита находилась щелевая диафрагма с размерами 0.8 мм × 35 мкм, а в 3.5 см перед ней – круглая диафрагма с радиусом отверстия 31 мкм. Сильное магнитное поле действовало не только в зазоре магнита, оно «выпячивалось» из входного и выходного торцов этого зазора. Обе диафрагмы были пробиты в лоскутках платиновой фольги – которые, будучи не ферромагнитными, практически, не искажали поле, которое «выпячивалось» навстречу летящим атомам. Т.е., на всей длине своего полёта в установке Штерна-Герлаха, атомы серебра продуцировали «щелчки» зарядовых разбалансов. Когда такой атом пролетал сквозь диафрагму не точно по центру, а ближе к какому-то её краю, каждый кратковременный ненулевой заряд атома индуцировал на этом краю диафрагмы заряд противоположного знака, и атом, из-за кулоновского притяжения, приобретал приращение вектора скорости, направленное к этому краю диафрагмы. Если в области щелевой диафрагмы, при магнитной индукции ~1 Тл, «щелчки» зарядовых разбалансов того или иного знака повторялись на частоте ~1 ГГц, то в области круглой диафрагмы, при индукции, на два порядка меньшей, соответствующая частота составляла ~10 МГц. Тогда, при скорости атома 470 м/с, на времени пролёта мимо кромки круглой диафрагмы, при её толщине 40 мкм, укладывалось всего два «щелчка» зарядовых разбалансов обоих знаков, а для щелевой диафрагмы эта цифра составляла ~200. На каждом таком «щелчке», атом получал поперечное приращение скорости d V, направленное к кромке диафрагмы:
где a - поперечное ускорение атома, t - длительность «щелчка» зарядового разбаланса, k - коэффициент эффективности индуцирования противоположного заряда, e - элементарный заряд, e0 - диэлектрическая проницаемость вакуума, s - эффективное расстояние между летящим атомом и индуцированным зарядом, m - масса атома. При этом, угол поворота траектории, набиравшийся за один щелчок «зарядового разбаланса, составлял da=d V/ V. Итоговый угол поворота Da определялся умножением da на количество N «щелчков» зарядовых разбалансов при пролёте мимо кромки, т.е.
где D - толщина диафрагмы, f - частота повторения «щелчков» зарядовых разбалансов. При ничтожном количестве этих «щелчков» на первой, круглой диафрагме, она не вносила значимых возмущений в проходящий пучок – разве что отклоняла медленные атомы, пролетавшие вблизи кромки, так что поток атомов, попадавший в щелевую диафрагму, имел пространственную селекцию по скоростям: вблизи правого и левого краёв диафрагмы, он был обеднён медленными атомами. Мы говорим о «медленных» атомах, потому что, по логике вышеизложенного, итоговый угол поворота траектории Da нелинейно зависел не только от близости пролёта к кромке диафрагмы, но и от скорости атома. А картина рассеяния (Рис.7.8) находит простое объяснение, если допустить, что в правый и левый концы щелевой диафрагмы влетают, преимущественно, быстрые атомы, а в её центральную часть влетают, преимущественно, медленные атомы – которые отклоняются к верхней и нижней кромкам диафрагмы сильнее, чем быстрые атомы. Но для такой пространственной селекции атомов по скоростям требуется не только вышеупомянутое обеднение медленными атомами потоков, попадающих в правый и левый концы диафрагмы, но и перевод в эти потоки быстрых атомов из центра пучка. А эта процедура выполняется в пучке механически: при большом разбросе по скоростям, в пучке происходят соударения атомов, вызывающие расширение пучка. Здесь можно говорить о поперечной диффузии атомов в пучке – а быстрые атомы диффундируют быстрее, чем медленные. Таким образом, допущение о пространственной селекции по скоростям у атомов, попадающих в щелевую диафрагму, и о кулоновском воздействии на них при пролёте сквозь неё – объясняет картину на Рис.7.8 качественно. Теперь приведём количественные оценки результирующих отклонений атомов в опыте Штерна и Герлаха – для «быстрых» атомов (V =670 м/с) и «медленных» атомов (V =270 м/с). При допущениях о том, что k =0.1 и t=10-11 с (7.8.1), результаты показаны в Таблице для двух значений s (7.8.1): 10 мкм и 1 мкм. Итоговое линейное смещение на стеклянной пластинке Dz находилось умножением угла Da на длину зазора магнита, равную 3.5 см.
Полученные оценки очень неплохо согласуются с реальной геометрией картины рассеяния (Рис.7.8). Особенность в виде выроста в сторону ножевого полюса магнита можно объяснить дополнительным кулоновским воздействием на атомы, летевших вблизи острия. Таким образом, именно наш подход объясняет, почему чудовищный разброс скоростей атомов в опыте Штерна и Герлаха не приводил к сплошному размыванию отпечатка пучка. Как можно видеть, отсутствием селекции скоростей атомов в опыте Штерна и Герлаха обеспечивался «момент истины». Если имело бы место силовое воздействие на спины атомарных электронов, то большой разброс скоростей атомов непременно дал бы сплошное размывание отпечатка пучка. А, поскольку такого размывания не обнаружилось, то опыт Штерна и Герлаха, вопреки распространённому мнению, наглядно продемонстировал, что спины атомарных электронов – даже если они существуют! – никак себя не проявили.
Ссылки к Разделу 7.
В1. С.В.Вонсовский. Магнетизм микрочастиц. «Наука», М., 1973. В2. С.В.Вонсовский. Современное учение о магнетизме. «Гос. изд-во технико-теоретической литературы», М., 1953. ВИД1. «Эпизод Е. Сегнетоэлектрики и электрофорная машина». – http://newfiz.info, папка «НАШИ ФИЛЬМЫ». Г1. А.А.Гришаев. Зарядовые разбалансы в «нейтральных» атомах. – http://newfiz.info/razbalan1.htm Г2. А.А.Гришаев. Новый взгляд на сущность эффекта Мёссбауэра. – http://newfiz.info/messbau.htm Е1. А.С.Енохович. Справочник по физике и технике. «Просвещение», М., 1976. И1. Ф.Иона, Д.Ширане. Сегнетоэлектрические кристаллы. «Мир», М., 1965. К1. С.Г.Калашников. Электричество. «Наука», М., 1977. К2. К.Б.Канн. Электродинамика. – Доступна на: http://electrodynamics.narod.ru Л1. Г.С.Ландсберг. Оптика. «Гос. изд-во технико-теоретической литературы», М.-Л., 1940. М1. Л.И.Мандельштам. Отклонения от законов Френеля. В: Лекции по оптике, теории относительности и квантовой механике. «Наука», М., 1972, с.392. П1. Р.В.Поль. Учение об электричестве. «Гос. изд-во физико-математической литературы», М., 1962. П2. Н.М.Померанцев, В.М.Рыжков, Г.В.Скроцкий. Физические основы квантовой магнитометрии. «Наука», М., 1972. Т1. И.Е.Тамм. Основы теории электричества. «Гос. изд-во технико-теоретической литературы», М., 1956. Т2. Таблицы физических величин. Справочник. Под ред. акад. И.К.Кикоина. «Атомиздат», М., 1976. Ф1. Физический энциклопедический словарь. Гл. ред. А.М.Прохоров. «Сов. энциклопедия», М., 1983. Ф2. Физические величины. Справочник. Под. ред. И.С.Григорьева, Е.З.Мейлихова. «Энергоатомиздат», М., 1991. Х1. А.Р.Хиппель. Диэлектрики и волны. «Изд-во иностранной литературы», М., 1960. Х2. Химия. Энциклопедия для детей, Т.17. «Аванта +», М., 2001. Ш1. W.Gerlach, O.Stern. Über die Richtungsquantelung im Magnetfeld. Annalen der Physik, 74 (1924) 673–699. Ш2. W.Gerlach, O.Stern. Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. Zeitschrift für Physik, 9 (1922) 349–352. Ш3. Э.В.Шпольский. Атомная физика. Т.1. «Наука», М., 1974.
Раздел 8. ХИМИЧЕСКАЯ СВЯЗЬ
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |


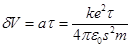
 , (7.8.1)
, (7.8.1)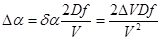 , (7.8.2)
, (7.8.2)


