Феномен сфер непроницаемости в атомах.

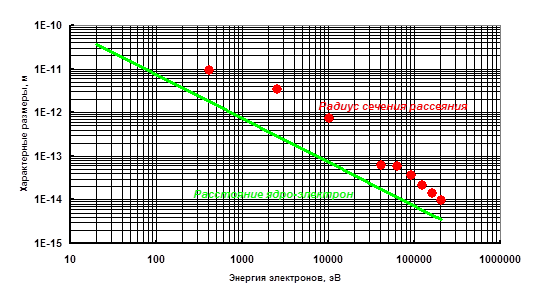
Характерный размер атома – несколько Ангстрем. По логике теоретиков, налетающий свободный электрон, с комптоновской длиной волны в 0.024 Ангстрема, с наибольшей вероятностью пронизывал бы атом насквозь, почти не встречая сопротивления. Но эти наивные ожидания опрокидываются опытом. Налетающие электроны натыкаются в атомах на то, что мы называем сферами непроницаемости [Г10]: они вложены друг в друга и имеют общий центр в центре атома – для проникновения в более глубокую сферу непроницаемости, электрон должен иметь всё большую кинетическую энергию. Если энергия налетающего электрона не превышает порогового значения, соответствующего той или иной сфере непроницаемости, электрон не может проникнуть внутрь этой сферы, а может лишь рассеяться на ней – упруго или неупруго. Образно говоря, сферы непроницаемости «цементируют» занимаемый атомом объём – и, чем ближе к ядру, тем это «цементирование» крепче.

Каждому электрону в атоме – а у них у всех разные расстояния от ядра – соответствует своя сфера непроницаемости, с центром в ядре и радиусом, равным расстоянию области удержания (6.4) электрона от ядра. Чем сильнее связан электрон, тем меньше его расстояние от ядра (см. (6.4.1)), и тем меньше радиус соответствующей сферы непроницаемости. Логично допустить, что пороговое значение кинетической энергии налетающего электрона, обеспечивающее его проникновение внутрь той или иной сферы непроницаемости, равно энергии связи атомарного электрона, которому соответствует та или иная сфера непроницаемости. Чтобы проникнуть в самую малую сферу непроницаемости и добраться до атомного ядра, налетающий электрон должен иметь кинетическую энергию, большую чем энергия связи самого сильно связанного атомарного электрона. Это подтверждается в опытах по зондированию атомов электронами – с определением соответствующих сечений рассеяния.

Действительно, при прохождении пучка электронов через газ, число электронов в пучке убывает по двум главным причинам: из-за упругого рассеяния электронов на частицах газа, а также из-за их неупругого рассеяния, при котором электроны теряют энергию на возбуждение и ионизацию атомов газа. Считается, что для энергий электронов от 10 КэВ и выше, «отклонение электронов почти полностью обусловлено упругими соударениями с атомными ядрами, в то время как потери энергии… происходят вследствие взаимодействия с электронами атомов» [К4].

Если согласиться с тем, что происходят «упругие соударения электронов с ядрами», то придётся признать два сопутствующих чуда. Первое чудо заключается в том, что «упругие соударения» электронов с ядрами возможны, если электроны отталкиваются ядрами, а не притягиваются, как это полагается при кулоновском взаимодействии зарядов противоположного знака. Поразительным образом, угловые распределения упруго рассеянных электронов [М7] тоже свидетельствуют о том, что происходит их отталкивание от рассеивающих препятствий, а не притяжение к ним. Речь о том, что эти угловые распределения содержат значимые количества рассеяний в обратную полусферу, вплоть до углов рассеяния 150^о (провести измерения на углах, более близких к 180^о, сложно технически). Обратное рассеяние легко объясняется как результат отскока от отталкивающего препятствия – например, от сферы непроницаемости – но в случае притягивающего центра придётся допустить, что электрон должен огибать его, набирая угол поворота вплоть до 180^о. На такие развороты никак не способны электроны с энергиями в несколько десятков эВ [Г10] – хотя и для таких электронов обратное рассеяние имеет место [М7]. Заметим, что теоретики нашли способ уйти от ответа на вопрос о том, притягивающее или отталкивающее действие на электрон оказывает рассеивающий центр. Применительно к угловым распределениям, говорят о «дифракции электронных волн на сферически симметричных рассеивающих атомах» [М7]. При таком подходе, действительно, можно забыть про то, что электроны несут электрический заряд.

Но даже такой подход не решает проблему. Ведь второе чудо, при допущении упругого рассеяния электронов на ядрах (размеры которых не зависят от энергии электронов), заключается в том, что сечение этого упругого рассеяния – которое как раз и характеризует размер рассеивающего препятствия – зависит от энергии электронов, и весьма сильно. Для подавляющего большинства химических элементов наблюдается следующее: при энергии налетающего электрона в несколько эВ, радиус сечения его упругого рассеяния близок к радиусу атома, а по мере увеличения энергии электрона, этот радиус уменьшается – вплоть до значений, близких к расстояниям от ядра у самых сильно связанных электронов. На диаграмме (Рис.6.5) точками обозначены радиусы сечения упругого рассеяния на основе экспериментальных данных (см. [Г10]); приведена также теоретическая зависимость (линия) расстояния от ядра у атомарных электронов, как функция их энергии связи, согласно (6.4.1).

 

Рис.6.5

 

Не выдерживает критики традиционное объяснение уменьшения сечения упругого рассеяния электронов при увеличении их энергии – которое апеллирует к соответствующему уменьшению их дебройлевской длины волны. Нас уверяют, что электроны – а, значит, и электронные волны – рассеиваются в атомах на ядрах, размеры которых одни и те же. При энергии электрона в несколько эВ, дебройлевская длина волны сопоставима с размером атома, и эта волна «не чувствует» ядро, т.е. препятствие с характерным размером на 5 порядков меньше. При энергии же электрона в сотню кэВ, дебройлевская длина волны составляет ~10^-12 м. Это меньше размера атома, но всё равно больше размера ядра на три порядка. Налицо ничтожность, по сравнению с длиной волны, размера препятствия – откуда же здесь быть рассеянию? Более того: теория волн гласит, что, при одних и тех же размерах препятствий, длинные волны рассеиваются меньше, чем короткие. Но если интерпретировать рассеяние электронов в терминах волн, то меньшее рассеяние более длинных электронных волн наблюдается лишь в некоторых инертных газах (Ar, Kr, Xe) в узком диапазоне энергий E ₀ электронов, 1 эВ £ E ₀ £ 10 эВ (вблизи области эффекта Рамзауэра [М7]) – а в огромном диапазоне энергий, E ₀ > 15 эВ, наблюдается меньшее рассеяние более коротких волн. Поэтому, на наш взгляд, некорректно говорить об эффекте Рамзауэра как о блестящем подтверждении волновой теории вещества. Ведь при этом умалчивается о том, что эффект Рамзауэра является жалким исключением из правила – по которому «электронные волны» ведут себя противоположно тому, как предсказывает волновая теория. Мы усматриваем здесь ещё одно свидетельство о том, что электроны волновыми свойствами не обладают (5.6).

Заметим, что выше мы говорили о проявлении феномена сфер непроницаемости в атомах только при столкновениях свободных электронов с атомами. Логично допустить, что этот феномен проявляется и при столкновениях атомов друг с другом: сферы непроницаемости задают границы занимаемых атомами объёмов, и, для всё более глубокого взаимопроникновения атомов, требуется всё большая энергия их столкновения.

Сферы непроницаемости в атомах, которые совершенно определённо проявляются в опытах, делают смехотворным расхожий тезис о том, что «атом, в основном, состоит из пустоты». В «пустоте» сферы непроницаемости действуют иные законы, чем в пустоте свободного от вещества пространства, и «пропуском» в сферу непроницаемости является энергия выше определённого порогового значения. Мы не представляем, как сферы непроницаемости в атомах могут порождаться чисто физическими свойствами. На наш взгляд, этот феномен порождается только соответствующими программными предписаниями.