Амплитудная модуляция квантовых пульсаций. Протон.

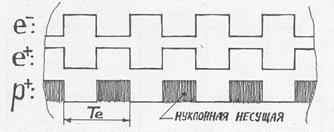
Временную развёртку квантовых пульсаций можно схематически проиллюстрировать меандром, т.е. прямоугольной волной; следует лишь иметь в виду, что амплитуда этой волны не имеет физического смысла – это подчёркивается тем, что энергия квантовых пульсаций зависит только от их частоты (1.4). Но если амплитуда квантовых пульсаций не имеет физического смысла, то очевидно, что амплитудная модуляция квантовых пульсаций может быть лишь стопроцентной по глубине, т.е. эта модуляция может заключаться лишь в периодическом «выключении», или прерывании, квантовых пульсаций.

Пусть квантовые пульсации на частоте f промодулированы с частотой прерываний B, (B << f). Пусть скважность прерываний равна 50%, т.е., на каждом периоде прерываний, в течение первого его полпериода происходят квантовые пульсации на частоте f, а в течение второго его полпериода эти пульсации отсутствуют. Модулированные таким образом квантовые пульсации, имеющие частоту f, пребывают в бытии лишь половину времени. Но при этом их энергия оказывается уменьшена отнюдь не вдвое, как это может показаться на первый взгляд. По необычным законам «цифрового» мира, энергия E _mod модулированных квантовых пульсаций, как мы полагаем, уменьшена на энергию, соответствующую частоте прерываний:

E _mod = hf - hB,                                                                                (5.2.1)

где h - постоянная Планка. Соответственно, масса квантового пульсатора, имеющего прерывания пульсаций, уменьшена на величину, эквивалентную энергии прерываний hB.

Теперь мы можем изложить наши представления о протоне. На наш взгляд, это квантовый пульсатор, имеющий модуляцию с электронной частотой (5.1) и фазой положительного электрического заряда (5.1); несущую же частоту протона, которая испытывает эти электронные прерывания, можно определить из того условия, что масса протона соответствует частоте, равной разности несущей и электронной частот, как следует из (5.2.1). При этом несущая частота протона составляет около 2.27×10²³ Гц, далее мы будем называть её нуклонной частотой (нуклонной несущей).

На Рис.5.2 схематически изображены дорожки квантовых пульсаций у электрона (e ^-), позитрона (e ⁺) и протона (p ⁺) – с учётом их фазовых соотношений (Т_е – период пульсаций на электронной частоте). В отличие от электрона и позитрона, протон имеет две частоты квантовых пульсаций: нуклонную, которой почти полностью соответствует масса протона,

 

Рис.5.2

 

и электронную, наличие которой означает наличие у протона элементарного электрического заряда – с фазой, соответствующей положительному заряду. При этом в протоне нет никаких суб-частиц: нельзя сказать, что он является соединением, например, массивного нейтрального керна и позитрона. Как можно видеть, объединение в протоне двух характеристических величин – массы, примерно в 1840 раз большей, чем у электрона, и элементарного заряда – реализовано простейшим, по логике «цифрового» мира, способом: через модуляцию квантовых пульсаций. Положительный заряд здесь не присоединён к большой нейтральной массе, а «вшит» в неё через модуляцию.

Будучи такой «сшивкой» двух квантовых пульсаторов, имеющих разные частоты, протон должен иметь и два характерных пространственных размера (1.4) – причём, объёмчики электронного и нуклонного пульсаторов протона должны перекрываться. Но их взаимное проникновение не должно вызывать проблемной ситуации неоднозначного программного управления (1.4). Эта проблема остро проявлялась бы для случая однотипных квантовых пульсаторов. Так, при совмещении двух свободных электронов и синхронизме их квантовых пульсаций, эти электроны были бы совершенно неразличимы для управляющих программ – не говоря уже о том, что два совмещённых квантовых пульсатора, которые пульсируют синхронно, должны вести себя, по цифровой логике, как один пульсатор, т.е. энергия (и масса) одного из них должна исчезнуть бесследно. Но эта проблема проявлялась бы тем менее остро, чем сильнее различались бы квантовые пульсаторы по своим частотам и, соответственно, по характерным размерам. Т.е., проблема взаимной непроницаемости остро проявляется при взаимодействии именно однотипных квантовых пульсаторов – например, при электрон-электронном рассеянии – но, начиная с некоторой разности по частотам и размерам квантовых пульсаторов, этой проблемы для них нет вовсе, и нет необходимости в их жёстком пространственном разделении. Это означает, что квантовые пульсаторы, достаточно сильно различающиеся по частотам и размерам, взаимопроницаемы и способны свободно проходить друг сквозь друга. Согласно нашей модели, само существование протона является иллюстрацией этого удивительного тезиса.