Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободная внутренняя термо-релаксация.
Если в теле создано неравенство максвелловской и планковской температур (10.2), и затем это тело предоставлено самому себе, то в нём начинается процесс самопроизвольного выравнивания этих двух температур. Этот процесс, по ходу которого состояние тела эволюционирует к термодинамически равновесному, мы будем называть свободной внутренней термо-релаксацией. Почему тело самопроизвольно стремится к термодинамическому равновесию? Ортодоксальная физика не даёт вразумительного ответа на этот вопрос, прикрываясь мистическими придумками вроде «закона неубывания энтропии». Такой трюк ничего не объясняет, а только переключает внимание с одной «непонятки» на другую, которая ещё хлеще первой. Между тем, вопрос проясняется, если учесть, что в игре участвуют две температуры – максвелловская и планковская (10.2) – а не одна, «просто температура», как это обычно полагают. В самом деле, если при взаимодействиях атомов изменялись бы энергии только в сопряжённых парах «энергии квантовых возбуждений – энергии связи» (т.е., в привычных терминах, если происходил бы только радиационный энергообмен), то, для такой ситуации, мы не усматриваем причин для того, чтобы неравновесное распределение по энергиям квантовых возбуждений самопроизвольно превращалось в равновесное. Аналогично, если, например, молекулы в газе испытывали бы только абсолютно упругие соударения, с сохранением суммы кинетических энергий до и после соударения – то, для такой ситуации, мы также не усматриваем причин для того, чтобы неравновесное распределение по кинетическим энергиям самопроизвольно превращалось в равновесное. Но эволюцию к равновесным распределениям энергий могут обеспечить взаимодействия, при которых у атомов происходят перекрёстные энергопревращения – с участием как энергий квантовых возбуждений, так и кинетических энергий. Такие взаимодействия известны: это, например, неупругие соударения частиц в газе. Они подчиняются законам сохранения энергии и импульса, но здесь допустимы определённые комбинации перераспределений энергий в обеих сопряжённых парах у участников соударения. Речь, например, об уменьшении кинетической энергии одного участника (и соответствующем увеличении его массы), и увеличении энергии квантового возбуждения у другого участника (и соответствующем уменьшении его энергии связи). Именно так, на наш взгляд, происходит столкновительное возбуждение атома. Но заметим, что задача о неупругом соударении имеет не единственное решение, а множество решений. И если перекрёстные перераспределения энергии при неупругих соударениях подчинены тем или иным правилам приоритета (программно заданным, (1.1)), то термодинамическое состояние может эволюционировать – причём, направление этой эволюции может быть задано этими правилами. Так, правила, задающие приоритет предельных случаев перекрёстных перераспределений – с минимизацией энергий квантовых возбуждений и соответствующим приростом кинетических энергий (или наоборот) – очевидно, уводили бы состояние от равновесного, поскольку усиливали бы рассогласования распределений в сопряжённых парах энергий и увеличивали бы несовпадение максвелловской и планковской температур. Нам представляется, что эволюцию состояния к равновесному обеспечивает алгоритм, по которому результатом неупругого соударения является, по возможности, выравнивание у участников как энергий тепловых квантовых возбуждений, так и кинетических энергий. Тогда распределения атомов по кинетическим энергиям и по энергиям тепловых квантовых возбуждений будут автоматически подстраиваться друг под друга, стремясь, соответственно, к максвелловскому и планковскому – и к совпадению максвелловской и планковской температур.
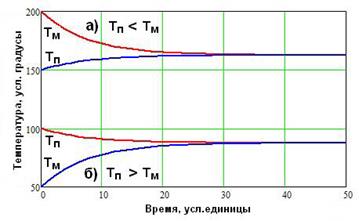
По логике вышеизложенного, вопрос «Что является источником теплового движения молекул?» так же нелеп, как и вопрос «Что является источником теплового возбуждения атомов?» Если тело имеет конкретную температуру выше абсолютного нуля, то, благодаря неупругим взаимодействиям, тепловое движение и тепловые возбуждения наличествуют в нём по определению, потому что они первичны, а соответствующие им температуры – вторичны. Важно отметить, что, при температуре T, наиболее вероятная, т.е. соответствующая максимуму распределения, кинетическая энергия молекулы есть kT [К5], где k – постоянная Больцмана, а наиболее вероятная энергия кванта теплового возбуждения есть 5 kT [Г18]. Значит, в процессе свободной внутренней термо-релаксации, когда максвелловская и планковская температуры (Т М и Т П, соответственно), сближаются так, чтобы стать равными при достижении равновесного состояния, максвелловская температура «подтягивается» к равновесному значению быстрее, чем планковская – что схематически иллюстрирует Рис.10.3. При этом, временем tрел свободной внутренней термо-релаксации можно назвать время, за которое исходная разность между значениями максвелловской и планковской температур уменьшится до средней величины флуктуаций температуры в равновесном состоянии.
Рис.10.3 Динамика максвелловской и планковской температур при свободной внутренней термо-релаксации.
Следует добавить, что принцип обеспечения свободной внутренней термо-релаксации – через перекрёстные превращения в двух сопряжённых парах энергии при неупругих взаимодействиях частиц – должен работать не только в газах, но и, например, в твёрдых телах. Ниже мы постараемся показать, что сама структура молекулярных кристаллов (10.7), а также механизм их теплового расширения (10.9), во многом определяются тесной связью между тепловыми квантовыми возбуждениями и тепловыми движениями молекул – главным типом которых, в данном случае, являются крутильные вибрации.
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 67; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.184.214 (0.004 с.) |