Раздел 2. Координатные поля и локально-абсолютные скорости

 

 

2.1 Непригодность концепции относительных скоростей для описания реалий физического мира.

«Скорости движения тел относительны, и нельзя сказать однозначно, кто относительно кого движется, ибо если тело А движется относительно тела В, то и тело В, в свою очередь, движется относительно тела А…»

 Эти умозаключения, насаждавшиеся нам ещё со школьной скамьи, выглядят безупречными с формально-логической точки зрения. Но, с физической точки зрения, они сгодились бы лишь для нереального мира, в котором отсутствуют ускорения. Неспроста Эйнштейн поучал, что СТО справедлива лишь для систем отсчёта (СО), «движущихся друг относительно друга прямолинейно и равномерно» [Э1] – впрочем, ни одной такой практической системы отсчёта он не указал. До сих пор никакого прогресса в этом вопросе не наблюдается. Не смешно ли, что, на протяжении более сотни лет, для базовой теории официальной физики не оговорена практическая область применимости?

А причина этой анекдотической ситуации весьма проста: в реальном мире, из-за физических взаимодействий, ускорения тел неизбежны. И тогда, попирая формальную логику, движение обретает однозначный характер: Земля обращается вокруг Солнца, ракета взлетает с Земли и выводит аппарат на траекторию полёта к Марсу, камешек падает на Землю, и т.д. Например, однозначность кинематики при падении камешка на Землю – т.е., нефизичность ситуации, при которой Земля падает на камешек – имеет подтверждение даже на основе закона сохранения энергии. Действительно, если при соударении камешка с Землёй скорость соударения составляет V, то кинетическая энергия, которая может быть превращена в другие формы, составляет при этом половину произведения квадрата скорости V на массу камешка, но уж никак не на массу Земли. Значит, эту скорость набрал именно камешек, т.е. названный случай адекватно описывается в СО, связанной с Землёй.

Но такая простая логика не устраивает релятивистов. Им никак нельзя соглашаться с тем, что бывают у тел такие ускорения, которые вызываются реальными физическими воздействиями на эти тела, а бывают у тел ускорения совсем другого рода – только из-за того, что СО, в которой эти ускорения обнаруживаются, сама движется ускоренно. Если признать эту разницу – понятную для ребёнка! – то концепции относительных скоростей очень не поздоровится. Поэтому общая теория относительности провозгласила равноправность всех СО – независимо от того, в каком состоянии движения они находятся. С тех пор нам пытаются втолковывать, что СО, связанная с падающим на Землю камешком, ничуть не хуже, чем СО, связанная с Землёй. Правда, в СО, связанной с камешком, Земля движется с ускорением g =9.8 м/с² и, набирая скорость, приобретает чудовищную кинетическую энергию. По логике релятивистов, движет Землю с ускорением g сила инерции, которая действует в СО, связанной с камешком. При этом релятивисты не утруждают себя объяснениями того, откуда у Земли берётся чудовищная кинетическая энергия, и куда эта энергия девается после того как Земля замирает, врезавшись в камешек. Вместо этих объяснений, нам подсовывают ставшую уже хрестоматийной дурилку про реальность сил инерции: если, мол, резко затормозит поезд, в котором ты едешь, дорогой читатель, то именно сила инерции швырнёт тебя вперёд и причинит увечья! У этого доходчивого разъяснения есть всего один недостаток: в нём умалчивается про то, что на причинение увечий здесь будет тратиться кинетическая энергия, опять же, пассажира, а не чего-то ещё. В этом можно легко убедиться: набрать исходную скорость самостоятельно, без помощи поезда – и с разгону налететь на столб или капитальную стену. Увечья выйдут ничуть не хуже – причём, без помощи всяких там сил инерции. Это мы к тому, что так называемые «реальные силы инерции», которые действуют только в ускоренных СО – это не более чем теоретические измышления. А истинно реальные физические процессы и реальные превращения энергии происходят независимо от того, в какой из СО проводится их теоретический анализ.

Более того, если вспомнить, что реальные превращения энергии должны происходить однозначно (1.3), то факт участия кинетических энергий в этих превращениях означает нечто поразительное. А именно: поскольку кинетическая энергия квадратична по скорости, то, при анализе ускоренного движения тела в различных СО, в которых мгновенная скорость тела различна, оказывается, что одно и то же приращение скорости даёт различные приращения кинетической энергии в различных СО. Из однозначности же приращений кинетической энергии следует, что мгновенная скорость тела тоже должна быть однозначна, т.е. адекватное описание движения тела должно быть возможно лишь в какой-то одной СО – в которой скорость тела является «истинной».

Кстати, однозначность приращений кинетической энергии пробного тела, в соответствии с приращениями его «истинной» скорости, была бы весьма проблематична, если тело притягивалось бы сразу к нескольким другим телам и, соответственно, приобретало бы ускорение свободного падения сразу к нескольким притягивающим центрам – как того требует закон всемирного тяготения. Например, если астероид испытывал бы тяготение и к Солнцу, и к планетам, то какова «истинная» скорость астероида, приращения которой определяют приращения его кинетической энергии? Вопрос нетривиальный. И, чтобы с ним не мучиться, гораздо проще разграничить области действия тяготения Солнца и планет в пространстве – так, чтобы пробное тело, где бы оно ни находилось, всегда тяготело лишь к какому-нибудь одному «притягивающему центру». Для этого нужно обеспечить, чтобы области действия тяготения планет не пересекались друг с другом, и чтобы в каждой области планетарного тяготения было «отключено» солнечное тяготение. При такой организации тяготения, т.е. по принципу его унитарного действия (3.8), простейшим образом решается проблема обеспечения однозначности приращений кинетической энергии пробного тела – а заодно и проблема отсчёта «истинных» скоростей физических объектов. Именно такой подход единым махом объясняет замалчиваемые официальной наукой факты, касающиеся движения астероидов (3.9) и межпланетных станций (2.6), аберрации света от звёзд (2.7), линейного эффекта Допплера при радиолокации планет (2.5), а также отсутствия «солнечных» гравитационных вариаций хода атомных часов на бортах спутников GPS (3.8).

Физики потратили немало усилий, пытаясь найти одну-единственную привилегированную СО – для адекватного определения абсолютных скоростей сразу всех физических объектов во Вселенной. Но эта задача, увы, была неверно поставлена. Опыт свидетельствует о том, что такой СО, одной для всей Вселенной, не существует, но зато существует иерархия СО для адекватного определения абсолютных скоростей – причём, рабочие области этих СО разграничены в пространстве, соответствуя разграничению областей действия тяготения больших космических тел. Принимая во внимание эту разграниченность, мы будем говорить не об абсолютных скоростях физических объектов, а об их локально-абсолютных скоростях (2.3), которые имеют чёткий физический смысл.

 

2.2  Координатные поля и мерность физического пространства.

Текущие координаты квантового пульсатора – это ключевые параметры, необходимые для работы его индивидуального пакета программ, которые обеспечивают его существование в физическом мире и управляют его поведением. Этими координатами определяется не только конкретное место, в котором производятся квантовые пульсации, но и текущее участие квантового пульсатора в физических взаимодействиях. Поэтому мы должны пояснить, как организованы системы координат, которыми оперирует программное обеспечение физического мира.

Заметим, что если объёмчики, занимаемые однотипными квантовыми пульсаторами, могли бы перекрываться – например, если два электрона могли бы совмещаться в физическом пространстве – то для объёма их перекрытия возникала бы ситуация двойного программного управления. Но, по логике однозначного программного управления (1.3), такая ситуация недопустима, поэтому программными средствами должна обеспечиваться уникальность индивидуальных координат однотипных квантовых пульсаторов. Для этого необходимо, чтобы программы работали с однозначными значениями координат, т.е. эти координаты непременно должны иметь абсолютный характер. Однако, абсолютный характер используемых координат вовсе не означает, что задействована одна-единственная система координат, охватывающая всю Вселенную. Можно организовать несколько разграниченных областей, в каждой из которых будет использоваться своя, независимая система абсолютных координат.

Есть прямые экспериментальные указания на то, что в Солнечной системе такая разграниченность организована следующим образом. Область действия солнечного тяготения имеет конечные размеры – граница проходит, с большой долей вероятности, по внешнему краю пояса Койпера, т.е. на радиусе ~48 а.е. [Г4]. В области действия солнечного тяготения, рабочей системой координат для программного обеспечения физического мира является гелиоцентрическая система координат. Именно гелиоцентрические положения и скорости имеют абсолютный, однозначный и совершенно чёткий физический смысл для пробных тел, находящихся в области действия солнечного тяготения. В частности, именно гелиоцентрические положения и скорости малого тела (астероида, кометы, межпланетного космического аппарата) являются теми параметрами, из которых выстраивается его кеплерова траектория при свободном полёте в межпланетном пространстве. Но, в области «солнечного» координатного поля имеются вычеты, где рабочими являются другие системы координат – это области планетарных координатных полей. Радиус области земного координатного поля – около 900 тыс. км. В пределах этой области, рабочей является геоцентрическая система координат, и однозначный абсолютный смысл имеют геоцентрические положения и скорости. На практике, для корректных расчётов полётов малых тел в околоземном пространстве, требуется использовать именно геоцентрические положения и скорости этих тел.

Таким образом, по разные стороны границы планетарного координатного поля, управляющие веществом программы используют разные системы координат: снаружи границы – гелиоцентрическую, а внутри границы – планетоцентрическую. Речь идёт не о пустой математической формальности – речь о том, что в пределах каждого координатного поля используется своя однозначная координатная привязка, необходимая для управления веществом. А координатная привязка – это не пустая формальность: из однозначных координат сразу следуют однозначные скорости, из однозначных скоростей – однозначные кинетические энергии. А из однозначности кинетических энергий сразу следует однозначность процессов, в которых происходят изменения этих энергий! Вот где разгадка тайны «инерциального фона» для однозначного отсчёта скоростей – это всего лишь координатные поля, которые используются программным обеспечением физического мира!

Фактически, эти координатные поля играют роль эфира, к необходимости наличия которого приходят мыслители, понявшие, что концепция относительных скоростей не выдерживает критики. Но эти мыслители полагают, что эфир является физическим объектом, материальной средой – и, из-за этого, работоспособную модель эфира не удаётся построить, поскольку его физические свойства оказываются слишком фантастическими и противоречивыми. Не будем перечислять противоречия, которые, практически, похоронили гипотезу о физическом эфире ещё в начале XX века. Обратим внимание вот на что: допуская физический эфир, мы сталкиваемся с той же самой его разграниченностью – область с припланетным эфиром движется (по орбите вокруг Солнца) сквозь межпланетный эфир, как целое, и при этом межпланетный и припланетный эфиры не должны смешиваться. Как такое возможно? – ведь не наблюдается никаких пограничных эфиродинамических эффектов: отсутствуют даже признаки обтекания, не говоря уже про турбулентность! Между тем, разграничить области с разными рабочими координатными полями и организовать беспроблемное перемещение одной области по другой – эта задача вполне решается программными средствами. Такое перемещение является чисто программной процедурой трансляции малого координатного поля по большому – с сохранением, в пределах малого поля, его собственного координатного формата.

Таким образом, вместо идеи о физическом эфире, ведущей в тупик, мы предлагаем новый путь. Модель координатных полей, которые использует программное обеспечение физического мира – это готовая модель эфира, свободная от противоречий в физических свойствах, поскольку этот эфир имеет природу не физическую, а надфизическую, программную. Похоже, именно этот эфир называется библейским термином «небесная твердь» - термин, на наш взгляд, исключительно удачен [Д1].

Добавим, что координатное поле, «с точки зрения» программ, которые его используют, представляет собой набор всех комбинаций координат, возможных для задаваемой этим полем области физического пространства. При этом, движение квантового пульсатора по физическому пространству – это всего лишь изменение значений координат в ячейках памяти, выделенных под эти значения. Заметим, что количество независимых координат, однозначно определяющих местоположение в физическом пространстве, определяет то, что называется мерностью физического пространства. Наше физическое пространство трёхмерно по простой причине – потому, что, для идентификации местоположений квантовых пульсаторов, программы используют тройки чисел. Именно к реалиям трёхмерного физического пространства приспособлено наше мышление [Н2].

При таком подходе к вопросу о мерности физического пространства, совершенно ясно, что эта мерность может иметь только целочисленное значение. Поэтому мы не относимся серьёзно к заявлениям иных теоретиков о том, что мерность физического пространства может быть меньше тройки на некоторую ничтожно малую величину, или к учению Н.Левашова о том, что тяготение порождается градиентами мерности (?!) пространства.

 

 

2.3 Что такое локально-абсолютная скорость.

С учётом вышеизложенных представлений о координатных полях (2.2), мы видим, что тело имеет целый набор своих положений и скоростей по отношению к другим телам (сколько других тел – столько относительных положений и скоростей, причём, всех сразу), но тело имеет совершенно однозначные положение и скорость по отношению к координатному полю, на котором оно находится. Поэтому однозначность протекания физических процессов, неизбежная при программном управлении ими (1.3), не обеспечивается через привязку к относительным координатам – она обеспечивается через привязку к абсолютным координатам, которые и реализуются с помощью координатных полей (2.2). Уместен вопрос: разве это можно называть «абсолютными» координатами? ведь разграниченных координатных полей – не два, не три, а гораздо больше, и у каждого – своя система координат! Отвечаем: каждое координатное поле задаёт систему именно абсолютных координат – но действующую только в пределах этого координатного поля. При пересечении границы между координатными полями, абсолютная координатная привязка переключается, но термин «локально-абсолютные координаты», на наш взгляд, адекватно описывает ситуацию – в каком бы координатном поле тело ни находилось.

Из понятия «локально-абсолютные координаты» логично следует понятие «локально-абсолютная скорость». Определение таково: вектор локально-абсолютной скорости – это вектор скорости относительно локального участка координатного поля. Может показаться, что такое определение не имеет никакой практической ценности. Координатное поле – это программная реальность… а как же, спрашивается, определять скорость тела относительно какой-то программной реальности?.. ведь ещё великий Мах учил, что на практике «мы можем проследить движение тела только относительно других тел»! К счастью, тела отсчёта для верного нахождения локально-абсолютных скоростей не нужно долго искать: Солнце и планеты покоятся в центрах своих координатных полей. Поэтому, в пределах планетарного координатного поля, искомым телом отсчёта является планета, а в межпланетном пространстве, не затронутом планетарными координатными полями, искомым телом отсчёта является Солнце.

При очевидном наличии тел отсчёта для верного нахождения локально-абсолютной скорости на практике, мы определяем её всё-таки по отношению к локальному участку координатного поля – потому что такое определение, на наш взгляд, более точно отражает реалии «цифрового» физического мира. Во-первых, координатные поля формируются чисто программными средствами и существуют независимо от физических тел – т.е., в принципе, подходящего тела отсчёта может и не быть. Во-вторых, именно координатными полями задаются области «инерциального фона» - или «небесной тверди», по отношению к которой имеет чёткий смысл та скорость движения физического объекта, которая является истинной-однозначной, т.е. локально-абсолютной. Чёткий смысл локально-абсолютной скорости проявляется даже в том, что движущееся тело имеет в себе четкий и однозначный признак того, что оно движется именно с этой скоростью: квантовые уровни энергии в атомах испытывают квадратично-допплеровские сдвиги – которые определяются квадратом именно локально-абсолютной скорости (2.8)!

Как же на практике верно отсчитывать локально-абсолютные скорости? В области земного координатного поля (радиус которой составляет около 900 тысяч километров), «небесная твердь» монолитно неподвижна по отношению к геоцентрической невращающейся системе отсчёта – несмотря на то, что область земного координатного поля движется по орбите вокруг Солнца, а Солнечная система каким-то образом движется в Галактике. Как можно видеть, в околоземном пространстве локально-абсолютной скоростью объекта является его скорость в геоцентрической невращающейся системе отсчёта. Если Вы, дорогой читатель, сейчас сидите за столом, т.е. покоитесь относительно земной поверхности, то Ваша локально-абсолютная скорость не равна нулю – она равна линейной скорости суточного обращения на Вашей широте и направлена на местный восток. Если же Вы движетесь относительно земной поверхности, то для нахождения Вашей локально-абсолютной скорости следует найти соответствующую векторную разность.

Заметим, что на практике уже существует удобная физическая реализация привязки к геоцентрической невращающейся системе отсчёта – с помощью таких спутниковых навигационных систем, как GPS. Плоскости орбит спутников GPS сохраняют ориентацию относительно «неподвижных звёзд», а Земля, в центре «розочки» этих орбит, совершает своё суточное вращение. Скорость самолёта в системе GPS – это именно локально-абсолютная скорость самолёта. На практике обычно требуется знать путевую скорость самолёта, т.е. горизонтальную составляющую его скорости относительно земной поверхности. Путевая скорость находится внесением в GPS-скорость соответствующей поправки на движение локального участка земной поверхности из-за суточного вращения Земли. Как можно видеть, для окрестностей Земли уже реализована процедура для измерения, в реальном времени, локально-абсолютных скоростей физических тел. В этой процедуре имелась важная практическая потребность. Именно вектор локально-абсолютной скорости космического аппарата требуется знать, чтобы корректно управлять его полётом – в особенности, если его траектория не является баллистической. Если при расчётах тяги и расхода топлива для выполнения манёвров использовать в качестве текущей скорости аппарата не локально-абсолютную, то его полёт по желаемой траектории и попадание в желаемый пункт назначения будут практически неосуществимы.

Следует добавить, что локальный участок координатного поля является «инерциальным фоном», по отношению к которому отсчитываются локально-абсолютные скорости не только физических тел. Скорость света в вакууме является фундаментальной константой тоже только в локально-абсолютном смысле. В частности, в области земного координатного поля, скорость света в вакууме ведёт себя как константа «с» лишь по отношению к единственной системе отсчёта – геоцентрической невращающейся – независимо от того, что область земного координатного поля каким-то образом движется в Солнечной системе и Галактике (4.11).

 

 

2.4 Правда про результат опыта Майкельсона-Морли.

Специальный принцип относительности, в переводе на общепонятный язык, утверждает, что никакими физическими опытами внутри лаборатории невозможно обнаружить её прямолинейное равномерное движение. То есть, в принципе невозможен прибор, который детектировал бы свою скорость автономно – без оглядки на «неподвижные звёзды» и навигационные спутники.

Согласно же излагаемому подходу, если скорость света «привязана» к локальному участку координатного поля, в котором он распространяется (2.3), то движущийся по этому же участку оптический прибор, способный «почувствовать» разницу скоростей света по ходу и против хода своего движения, вполне способен выявить свою скорость – причём, одну-единственную, локально-абсолютную (2.3). Способный на это прибор, покоясь на земной поверхности, не дал бы отклик ни на скорость орбитального движения Земли вокруг Солнца, ни на скорость собственного движения Солнечной системы в Галактике. Единственная скорость, на которую он дал бы отклик – это его линейная скорость из-за вращения Земли вокруг своей оси. Потому что для такого прибора имел бы место лишь один «эфирный ветерок» – дующий с востока со скоростью, равной линейной скорости суточного вращения земной поверхности на местной широте.

Вспомним: официальная история физики повествует о том, что упорные поиски эфирного ветра не увенчались успехом. Ключевым здесь считается опыт Майкельсона-Морли. Схема интерферометра Майкельсона, идея опыта и расчёт разности хода лучей приведены во множестве учебных пособий, и мы на этом останавливаться не будем. Широко известно об «отрицательном результате» опыта Майкельсона-Морли: никакого эфирного ветра, якобы, не обнаружилось. Это неправда. Опыт был нацелен на выявление эфирного ветра, обусловленного орбитальным движением Земли вокруг Солнца – и вот он, действительно, не обнаружился. Но ведь обнаружился «эфирный ветерок» с востока!

Действительно, С.И.Вавилов [В1] обработал результаты опыта Майкельсона-Морли 1887 года [М1] и рассчитал наиболее достоверные сдвиги интерференционных полос, в зависимости от ориентации прибора. Из-за орбитального движения Земли, со скоростью 30 км/с, там ожидался эффект с размахом в 0.4 полосы. Цифры Вавилова демонстрируют волну с размахом 0.04-0.05 полосы, причём горбы и впадины этой волны соответствуют ориентациям плеч прибора в направлениях «север-юг» и «запад-восток» – независимо от времени суток и времени года.

Официальная наука уклоняется от обсуждения этого впечатляющего эффекта. Мы же попробуем его объяснить. При длине плеча L =11 м, длине волны l=5700 Ангстрем, и скорости прибора V =0.35 км/с (на широте Кливленда), сдвиг на 0.05 полосы слишком велик, чтобы объяснить его на основе традиционного расчёта, дающего для ожидаемого сдвига полос величину (2 L /l)(V ²/ c ²), где c - скорость света. Но мы обратили внимание на следующее: от эксперимента к эксперименту по схеме Майкельсона-Морли наиболее сильно варьировалась длина плеча, причём увеличенные «ненулевые» результаты, в частности, у Миллера, получались как раз при увеличенных длинах плеч. Не могло ли оказаться так, что некоторый эффект, зависящий от длины плеч, не принимался в расчёт?

Обратим внимание: интерферометр Майкельсона-Морли имеет ненулевой угол клина, т.е. угол между плоскостями эквивалентной воздушной прослойки. Ненулевой угол клина g и, соответственно, ненулевой угол схождения интерферирующих лучей 2g требуются здесь для того, чтобы интерференционная картинка представляла собой полосы равной толщины, а не полосы равного наклона. Наш анализ [Г1] показывает, что, из-за ненулевого угла клина, разностный сдвиг интерференционных полос при двух вышеназванных характерных ориентациях прибора составит D n» 4 L g(V / c)/l. Поскольку экспериментаторы не принимали во внимание этот эффект, они не сообщали о величине угла клина. Но если подставить в это выражение для D n названную Вавиловым величину 0.05, а также вышеприведённые значения остальных параметров, то для угла клина мы получим цифру g»5.5×10^-4 рад. Такая величина для угла клина интерферометра Майкельсона представляется нам совершенно реалистичной. Поэтому можно допустить, что Майкельсон и Морли в эксперименте 1887 года, фактически, продетектировали локально-абсолютную скорость прибора.

Да и на что ещё мог реагировать прибор Майкельсона-Морли, кроме как на свою локально-абсолютную скорость? Это же не интерферометр Саньяка, в котором свет движется во встречных направлениях в обход контура с ненулевой площадью, благодаря чему детектируется собственное вращение прибора. У интерферометра Майкельсона-Морли площадь контура нулевая! И это не акселерометр, который используется, например, в системах инерциальной навигации – где детектируется ускорение, а затем оно интегрируется, и, таким образом, вычисляется скорость. Нет, прибор Майкельсона-Морли реагировал непосредственно на свою скорость, повергая в прах принцип относительности. Вот почему релятивисты помалкивают про эфирный ветерок с востока, который обнаружился у Майкельсона и Морли – но, наоборот, громко кричат о том, что не обнаружился эфирный ветер из-за орбитального движения Земли.

Само собой, этот обман им пришлось подкреплять ещё целой вереницей обманов, которые на их языке называются «аналогами опыта Майкельсона-Морли». Эти «аналоги» - целый ряд выполненных по разным схемам опытов, в которых результаты поиска эфирного ветра оказались, практически, полностью нулевыми, как будто этот ветер отсутствовал совершенно. То, что в этих опытах никак не проявилось орбитальное движение Земли – это само собой. Но почему там не проявилось движение установки из-за вращения Земли вокруг своей оси? Потому что это не-проявление было обусловлено либо метрологически, либо методологически. То есть, либо была недостаточна точность опыта, чтобы обнаружить эфирный ветерок с востока, со скоростью ~300 м/с, либо сама постановка опыта была такова, что обнаружение этого ветерка принципиально исключалось.

Так, Эссен [Э2] искал вариации частоты полого цилиндрического резонатора на 9200 МГц, которые имели бы место при изменениях его ориентации по отношению к линии эфирного ветра. При горизонтальном положении оси резонатора, он поворачивался в горизонтальной плоскости, делая оборот за минуту. Через каждые 45^о поворота, частота резонатора измерялась с помощью кварцевого стандарта. Относительная разность частот резонатора для положений вдоль и поперёк линии эфирного ветра составляла бы (1/2)(V ²/ c ²). Для скорости эфирного ветра V =30 км/с, эффект составил бы ~5×10^-9. Данные Эссена демонстрируют волну с размахом на порядок меньше. Такая волна свидетельствовала об отсутствии «орбитального» эфирного ветра. Но происхождение самой этой волны осталось невыясненным – причём, в её присутствии, не было шансов обнаружить волну из-за «суточного» эфирного ветра, с размахом на три порядка меньшим.

Таунс с сотрудниками [Т1] измеряли частоту биений у пары мазеров на аммиаке, установленных пучками молекул навстречу друг другу – причём, вдоль линии «запад-восток». Затем разворачивали установку на 180^о и вновь измеряли частоту биений. Эти измерения проводились на протяжении более полусуток, чтобы Земля повернулась более чем на пол-оборота вокруг своей оси. «Орбитальный» эфирный ветер при такой методике обнаружился бы, а «суточный» - нет, поскольку, при развороте установки, допплеровские сдвиги частот у мазеров просто менялись ролями, и частота биений оставалась прежней.

Ещё в одном эксперименте, выполненном под руководством Таунса [Т2], исследовалась частота биений двух ИК-лазеров, с ортогонально расположенными резонаторами, при поворотах установки на 90^о между положениями, в которых один резонатор ориентирован по линии «север-юг», а другой – по линии «запад-восток». Принималось, что у резонатора, ориентированного параллельно «эфирному ветру», частота есть f ₀(1-b²), а у резонатора, ориентированного ортогонально «эфирному ветру», частота есть f ₀(1-b²)^1/2, где f ₀ – невозмущённая частота, b= V / c. Поскольку f ₀=3×10¹⁴ Гц, то из-за скорости 30 км/с можно было ожидать разностный эффект с размахом 3 МГц. Размах же обнаруженного эффекта составил всего 270 кГц, причём он почти не зависел от времени суток, хотя проявлению «эфирного ветра» из-за орбитального движения Земли следовало быть максимальным в 0 и 12 часов, а минимальным – в 6 и 18 часов местного времени. Обнаруженный эффект интерпретировали как результат магнитострикции в металлических стержнях резонаторов из-за влияния магнитного поля Земли. Линейная скорость из-за суточного вращения дала бы здесь эффект с размахом около 300 Гц, который был бы сфазирован с эффектом от магнитострикции и тоже не зависел бы по величине от времени суток – а, значит, его не-обнаружение было обусловлено даже методологически.

В особую группу можно выделить эксперименты, в которых обеспечивалась весьма высокая точность измерений – но, увы, ориентация всех элементов установки относительно земной поверхности была постоянна. Конечно, там не могло быть никаких разностных эффектов из-за линейной скорости суточного вращения. Поэтому оно никак не проявилось, например, в эксперименте с использованием стандарта частоты на охлаждённых ионах [П1], или при спектроскопии двухфотонного поглощения в атомном пучке [Р1], или при сличениях частот двух лазеров видимого диапазона, стабилизированных разными способами [Х1].

Между тем, при достаточной точности измерений и корректной методике, линейная скорость лаборатории из-за суточного вращения Земли успешно детектируется. Мы расскажем о двух таких экспериментах.

Чемпни и соавторы [Ч1] разместили мёссбауэровские излучатель и поглотитель (Co⁵⁷ и Fe⁵⁷) на диаметрально противоположных участках ротора ультрацентрифуги, вращаемой в горизонтальной плоскости. Один детектор гамма-квантов был установлен с северной стороны от ротора, второй – с южной. Детекторы были прикрыты свинцовыми экранами с диафрагмами, пропускавшими лишь те кванты, которые шли в узком створе, соосном с линией «излучатель-поглотитель», когда эта линия была ориентирована в направлении

 

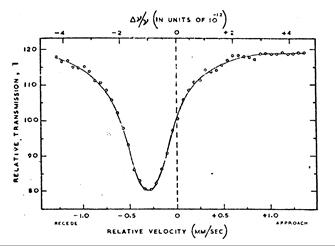
Рис.2.4.1

 

«север-юг». Пик резонансного поглощения на 14.4 кэВ, заранее полученный линейно-допплеровским методом (см. Рис.2.4.1), соответствовал скорости расхождения излучателя и поглотителя ~0.33 мм/с, при этом энергия рабочего перехода у поглотителя была меньше, чем у излучателя, на ~1.1×10^-12. Идея опыта была основана на том, что если абсолютные скорости в эфире имеют физический смысл, то, при движении установки в эфире (расчёт был, опять же, на орбитальное движение Земли) вращение ротора даст неравенство абсолютных скоростей излучателя и поглотителя. Соответственно, их линии приобретут неодинаковые квадратично-допплеровские сдвиги. Так, пусть лаборатория движется в эфире на восток, а ротор вращается против часовой стрелки, если смотреть на него сверху. Тогда северный счётчик будет считать кванты в условиях, когда линейная скорость вращения излучателя складывается со скоростью установки в эфире, а линейная скорость вращения поглотителя – вычитается из неё. Из-за результирующих квадратично-

 

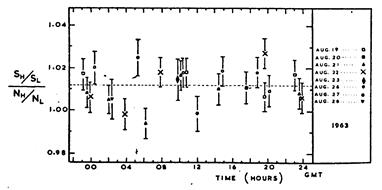
Рис.2.4.2

 

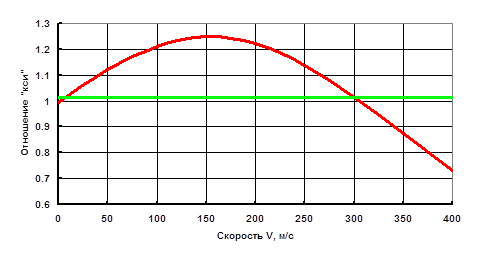
допплеровских сдвигов, линии излучателя и поглотителя сдвинутся друг к другу, отчего поглощение увеличится, т.е. скорость счёта уменьшится. Соответственно, для южного счётчика всё будет наоборот. В итоге опыт позволял сделать вывод о том, абсолютные или относительные скорости имеют физический смысл. Действительно, при каждом цикле измерений использовались две скорости вращения ротора – 200 Гц и 1230 Гц – дававшие линейные скорости вращения 55.3 и 340 м/с. Измерялись четыре величины: скорость счёта северного счётчика при малой и большой скоростях вращения, N _L и N _H, и, аналогично, для южного счётчика, S _L и S _H – и находилось отношение x=(S _H/ S _L)/(N _H/ N _L). При справедливости концепции относительных скоростей, отношение x было бы, с точностью до погрешностей, равно единице. При справедливости же концепции абсолютных скоростей, отношение x отличалось бы от единицы – причём, если бы имел место эфирный ветер из-за орбитального движения Земли, x зависело бы от времени суток. Как показывают результаты [Ч1], которые мы воспроизводим (см. Рис.2.4.2), x близко к единице и не зависит от времени суток – т.е. орбитальный эфирный ветер никак не проявился. Вместе с тем, среднее по приведённому набору данных составляет, как можно видеть, 1.012. Не свидетельствует ли этот результат об эфирном ветерке из-за суточного вращения Земли?

Если обозначить скорость этого ветерка через V, то квадратично-допплеровские расхождения линий излучателя и поглотителя для южного счётчика и, наоборот, их сближение для северного счётчика, составит величину D=2 Vv / c ², где v – линейная скорость вращения излучателя и поглотителя. Используя график (см. Рис.2.4.1), мы нашли аппроксимации для функций скоростей счёта обоих счётчиков от скорости V – для меньшей и большей вышеназванных скоростей v. При меньшем значении v мы использовали линейную аппроксимацию, для S _L(V) и N _L(V), а при большем – квадратичную аппроксимацию, для S _H(V) и N _H(V). Вышеназванная комбинация этих четырёх функций даёт зависимость отношения x от V, которая приведена на Рис.2.4.3.

Рис.2.4.3

 

Как можно видеть, на этом графике значение x=1.012 соответствует двум значениям V: 6.5 и 301 м/с. Для первого из них мы не усматриваем физического смысла, а второе всего на 7.9% отличается от 279 м/с – линейной скорости суточного вращения на широте Бирмингема, где проводился опыт. Едва ли можно сомневаться в том, что авторы [Ч1] продетектировали локально-абсолютную скорость лаборатории – но, странным образом, они проигнорировали этот результат.

Ещё один эксперимент, где проявилась локально-абсолютная скорость лаборатории, провели Брилет и Холл [Б1]. Они разместили гелий-неоновый лазер (3.39 мкм) и внешний

 

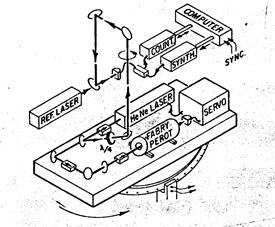
Рис.2.4.4

 

резонатор Фабри-Перо, по которому лазер был стабилизирован, на медленно вращающейся платформе (см. Рис.2.4.4). Частота этого лазера сравнивалась с частотой невращающегося гелий-неонового лазера, стабилизированного по линии поглощения в метане. Авторы утверждали, что эффект от «эфирного ветра» не превышал 0.13±0.22 Гц, или (1.5±2.5)×10^-15. Между тем, они наблюдали стойкий систематический эффект на второй гармонике частоты вращения платформы, с амплитудой 17 Гц (2×10^-13), причём фаза этого эффекта была строго согласована с ориентацией платформы относительно лаборатории. О магнитострикции речь не шла, поскольку зеркала внешнего резонатора были посажены на торцы трубки из стеклокерамики, к тому же резонатор был экранирован. Источник эффекта на второй гармонике остался невыясненным, и авторы везде говорили об этом эффекте как о паразитном. Давайте посмо