
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автономные превращения энергии квантовых пульсаторов.Содержание книги
Поиск на нашем сайте
Теоретики приписывали статус физической реальности объектам с совершенно фантастическими энергетическими характеристиками. Так, удивительной находкой оказалась идея о физических полях – гравитационном, электромагнитном – с их бесконечными числами степеней свободы, а, значит, и с бесконечным энергосодержанием. Впоследствии физические поля проквантовали – и назвали «физическим вакуумом» состояние полей с минимальной возможной энергией (которая всё равно осталась бесконечной). Ещё больше оживили физическую картину мира «виртуальные частицы», которыми, якобы, бурлит физический вакуум. На этих виртуальных частиц теоретики имеют обыкновение сваливать ответственность за разного рода энергетические парадоксы – ведь виртуальная частица, якобы, способна произвести в локальности как угодно большое отклонение от закона сохранения энергии. Правда, такое отклонение длится, в согласии с принципом неопределённости, исключительно недолго – но теоретикам и этого хватает для решения своих проблем. В реальном физическом мире подобный произвол с энергиями не имеет места. Мы сознательно устраняем «энергетических паразитов» из понятийного базиса физики и утверждаем, что обладателем всех форм физической энергии является только вещество. Причём, каждая форма физической энергии соответствует конкретной форме движения в веществе. По логике «цифрового» мира, элементарные частицы вещества представляют собой квантовые пульсаторы (1.4). У квантового пульсатора мы усматриваем три основных формы энергии. Главная из них – собственная энергия; соответствующая ей форма движения – это квантовые пульсации. Вторая из них – кинетическая энергия; соответствующая ей форма движения – это, очевидно, перемещение в пространстве. Наконец, третья из них – это энергия связи (если частица входит в состав некоторой структуры); соответствующая форма движения – это циклические перебросы квантовых пульсаций из одной связуемой частицы в другую (6.2). Чтобы выполнялся закон сохранения энергии, для трёх названных форм энергии квантового пульсатора должна быть обеспечена беспроблемная и однозначная превращаемость друг в друга. При этом однозначность кинетической энергии обусловлена тем, что она определяется однозначной, «истинной» скоростью частицы – а именно, её локально-абсолютной скоростью (2.3) (ниже, говоря о скорости частицы V, мы будем подразумевать именно локально-абсолютную скорость). Вот эти обратимые взаимопревращения собственной энергии, кинетической энергии и энергии связи у элементарной частицы вещества мы называем автономными превращениями энергии квантового пульсатора. Заметим, квантовый пульсатор может не иметь кинетической энергии и энергии связи, но собственная энергия у него есть обязательно. Учитывая, что только квантовые пульсаторы являются носителями физических энергий, мы приходим к выводу: «необязательные» формы энергии могут быть у квантового пульсатора лишь при соответственно уменьшенной «обязательной» - т.е., за её счёт. У каждого квантового пульсатора сумма трёх энергий – собственной энергии, кинетической энергии и энергии связи – остаётся постоянной (при постоянном гравитационном потенциале). И всё многообразие физических процессов сводится к тому, что, в результате тех или иных взаимодействий, происходят перераспределения между тремя формами энергии у квантовых пульсаторов – по принципу их автономных превращений. Так, свободная элементарная частица может иметь кинетическую энергию только за счёт точно такой же убыли своей собственной энергии. Это непривычно, ведь многовековой опыт учит нас: чтобы разогнать тележку, нужно совершить работу и сообщить тележке кинетическую энергию. Этот штамп – «сообщить кинетическую энергию» – прочно вошёл в учебники по физике. Он однозначно подразумевает, что кинетическая энергия может быть сообщена разгоняемому объекту лишь откуда-то извне. Но в микромире, на уровне элементарных частиц, эта логика не работает. Как ни старайтесь, вы не сможете сообщить элементарной частице кинетическую энергию. Вы сможете лишь превратить в её кинетическую энергию часть её собственной энергии. Потому что так работают программные предписания: у элементарной частицы других вариантов приобретения кинетической энергии не предусмотрено. Получим выражение для кинетической энергии E кин свободного квантового пульсатора – на основе принципа автономного превращения. Принимая, что прирост кинетической энергии обусловлен убылью собственной энергии, имеем:
где m 0 - масса свободного покоящегося квантового пульсатора, V - его скорость. Из (1.5.1) получаем искомое выражение: Соответственно, собственная энергия E соб свободного квантового пульсатора, как функция его скорости, имеет вид: Обращает на себя внимание сходство формул (1.5.2) и (1.5.3), в которых привычные выражения помножены на одну и ту же дробь, в которую входит квадрат скорости. Эти формулы наглядно показывают, что по мере увеличения скорости, собственная энергия квантового пульсатора даже не остаётся постоянной – она, частично превращаясь в кинетическую энергию, уменьшается. Причём, в случае V= c кинетическая энергия свободного квантового пульсатора составит одну треть (а собственная энергия – две трети) от его собственной энергии покоя. Таким образом, из этих формул следует, что, по мере увеличения скорости, собственная энергия (а, значит, и масса) квантового пульсатора не испытывает релятивистского роста. Но не спешите, дорогой читатель, ставить крест на этих формулах. Да, всем нам со школьной скамьи вдалбливали, что релятивистский рост массы (энергии, импульса) – есть, есть, есть! Это, заметьте, при том, что, в отличие от нашего подхода, в официальной физике до сих пор нет определения того, что такое масса, и нет внятного физического обоснования – с какой стати масса должна расти при увеличении скорости. Поэтому релятивисты апеллируют только к опыту – релятивистский рост массы, мол, это экспериментальный факт! Но это ложь: экспериментальные реалии говорят совсем другое (1.6). А правда в том, что в кинетическую энергию свободного электрона превращается его собственная энергия, и никакая другая. Ортодоксам трудно в это поверить. Они полагают, что в кинетическую энергию электрона превращается энергия ускоряющих его электромагнитных полей. Именно это, якобы, проделывается на ускорителях заряженных частиц. Логика убийственная: электроны ускоряются лишь тогда, когда электромагниты включены – значит, ускоряются-то они на энергиях полей! И, чтобы стать ультрарелятивистскими, ускоряемые электроны должны накрутить многие километры!.. Да мы не оспариваем то, что на ускорителях электроны накручивают километры. Мы лишь напомним, что в природе есть способ гораздо более эффективного разгона электрона. Вот он: при бета-распаде [Д2] из ядра выстреливается готовый релятивистский электрон. Спрашивается: что это за чудовищные поля генерируются в ядре – которые, к тому же, избирательно действуют лишь на выстреливаемый электрон? А если не поля – то что? Не маленькие же зелёные человечки с кувалдами! «Моментальный» разгон электрона при бета-распаде остаётся тайной для науки. По традиционной логике, здесь кинетическая энергия должна быть откуда-то сообщена электрону. Поэтому полагают, что в его кинетическую энергию превращается часть разности энергий связи исходного и результирующего ядер. Но как это происходит – и происходит ли вообще! – об этом не сообщается. Принцип автономных превращений энергии позволяет по-новому взглянуть на эту проблему. Но прежде скажем о том, как мы представляем алгоритм пространственного перемещения свободного квантового пульсатора. Если сущностью квантового пульсатора является циклический скачкообразный процесс, то логично предположить, что и перемещаться в пространстве он может лишь скачкообразно. Движение квантового пульсатора с постоянной скоростью означает, что, через некоторое постоянное число собственных циклов, он совершает элементарное скачкообразное перемещение – длина которого, как мы полагаем, равна характерному размеру квантового пульсатора, т.е. его комптоновской длине. Такое элементарное перемещение мы называем квантовым шагом. Частота квантовых шагов W равна, как можно видеть, отношению скорости движения к длине квантового шага, т.е. к комптоновской длине lС, которая, с учётом (1.5.3), также зависит от скорости:
Как можно видеть из (1.5.4), по мере роста скорости частота квантовых шагов W растёт, и при V= c она становится равной собственной частоте пульсатора. Ясно, что частота квантовых шагов не может превышать собственной частоты пульсатора, поэтому не представляется возможным его движение со скоростью, превышающей c (что же касается относительных скоростей – например, у пары движущихся друг навстречу другу квантовых пульсаторов – то эти скорости должны подчиняться классическому закону сложения скоростей, т.е., они могут превышать с). Теперь вернёмся к «моментальному» разгону электрона при бета-распаде. Алгоритм, который осуществляет превращение собственной энергии электрона в кинетическую, работает, по логике вышеизложенного, с дискретом во времени, соответствующим периоду пульсаций электрона. И такое превращение – хоть даже на максимально допустимую величину – может произойти, в принципе, за один цикл работы этого алгоритма. И – полетел он, релятивистский электрон! Уточним, что, согласно принципу автономных превращений энергии, частица вещества не может ни отдать часть своей энергии вовне, ни получить добавочную энергию извне. Казалось бы, этот подход противоречит опыту – ведь при многих взаимодействиях, как полагают, происходит передача энергии от одного микрообъекта другому. Но при ближайшем рассмотрении оказывается, что во всех этих случаях вполне может происходить не передача энергии, а её согласованные автономные превращения, порождающие иллюзию передачи. Например, говорят, что, при столкновениях частиц, налетающая частица передаёт покоящейся частице свою кинетическую энергию. В рамках же нашего подхода, при таком столкновении полные энергии каждой из частиц не изменяются, а происходят равные по величине и противоположные по направлению перераспределения между собственной и кинетической энергиями у каждой из этих частиц. Аналогично, при ударном возбуждении атома ударяющий электрон отнюдь не отдаёт атому свою кинетическую энергию, которая превращается в энергию возбуждения атома. При этом, как мы полагаем, у ударяющего электрона уменьшается кинетическая энергия и, соответственно, увеличивается собственная, а у атома – уменьшается энергия связи и, соответственно, тоже увеличивается собственная. Если происходит ударная ионизация, то сначала энергия связи обнуляется, с соответствующим восстановлением собственных энергий, а затем освобождённый электрон ещё и может быть приведён в движение – с превращением части его собственной энергии в кинетическую. Сходным образом, дело обходится без передачи энергии от атома к атому, когда при их соударении происходит столкновительный перенос возбуждения. Наконец, при квантовом перебросе световой энергии с атома на атом происходят, как мы полагаем, всего лишь скоррелированные перераспределения энергии у этой пары атомов (4.12). Подчеркнём, что автономные превращения энергии происходят со стопроцентным коэффициентом полезного действия, совершенно без потерь энергии. Так, при ускорении элементарной частицы вещества гравитационным или электромагнитным воздействием, не происходит диссипации энергии. Напротив, если говорить про двигатели, в которых сжигается топливо, то они производят почти стопроцентную диссипацию, которая сопровождается жалким побочным продуктом – автономным приростом кинетической энергии у частиц приводимого в движение аппарата. Насколько возросли бы возможности техники, если бы в ней использовался прямой доступ к алгоритмам, управляющим автономными превращениями энергии!
1.6 Где же он, релятивистский рост массы (энергии, импульса)? Тезис о том, что кинетическая энергия элементарной частицы не может превышать одной трети от её энергии покоя (1.5), кажется смешным с позиций современной официальной физики – особенно в свете достижений ускорительной техники, где, как нас уверяют, электронам, имеющим энергию покоя в полмиллиона эВ, сообщают кинетические энергии, исчисляемые миллиардами эВ. «Если бы не было релятивистского роста массы, - вещают с телевизионных экранов академики, - то не работал бы ни один ускоритель!» Для домохозяек такие аргументы – вполне убедительны. Они же не знают, как эти ускорители «работают». А если бы узнали – ужаснулись бы. Вот, спрашиваем: как на ускорителях проявляется релятивистский рост массы? Да, отвечают, всё так же, одним-единственным способом: через уменьшение эффективности воздействия электромагнитных полей на быстро движущуюся заряженную частицу – как и в самых первых опытах такого рода с быстрыми электронами (опыты Бухерера, Кауфмана и др.; см., например, [С2,Д3]). Чем больше скорость электрона, тем более сильное магнитное воздействие требуется приложить, чтобы искривить его траекторию. При большом желании, результаты этих опытов, действительно, можно истолковать так: по мере увеличения скорости частицы, у неё увеличивается масса, а вместе с ней и инертные свойства – так что магнитное воздействие на такую частицу вызывает всё меньший отклик. Но такое толкование уместно, и вправду, только при большом желании – ведь здесь, как говорится, возможны варианты! Известен универсальный принцип: воздействие на объект стремится к нулю, если скорость объекта приближается к скорости передачи воздействия. Вот классический пример из механики: ветер разгоняет парусник. Когда скорость парусника становится равной скорости ветра, ветер перестаёт на него действовать. Даже детям понятно: это получается не оттого, что масса парусника становится бесконечной. Аналогичные вещи происходят при раскрутке ротора асинхронной машины вращающимся магнитным полем, а также при взаимодействии электронов с замедленной электромагнитной волной в лампе бегущей волны – и здесь, как полагают, массы тоже остаются самими собой. Лишь для методики магнитного отклонения заряженной частицы делается исключение – здесь, мол, не что иное, как релятивистский рост! На основании чего делается такое исключение? Скорость заряженной частицы может быть измерена с помощью различных методик, напрямую реализующих понятие скорости, т.е. основанных на измерении промежутка времени, в течение которого преодолевается известное расстояние. Если на заряженную частицу, движущийся с измеренной скоростью V, подействовать поперечным магнитным полем с напряжённостью H, то частица станет двигаться по траектории с радиусом кривизны r:
где m и e - соответственно, масса покоя и заряд частицы, g - релятивистский фактор. Анализ искривлений треков сталкивающихся частиц показывает, что сохраняется сумма их релятивистских импульсов m V g. Раз сохраняется релятивистский импульс – значит, мол, он и реален! Но ведь те же самые трековые данные допускают и другую интерпретацию. Если считать, что релятивистский корень в (1.6.1) описывает уменьшение напряжённости магнитного поля, которое воспринимает движущийся электрон – в согласии, заметим, с релятивистскими преобразованиями компонент поля [Л2]! – то наблюдаемый радиус кривизны траектории будет соответствовать не истинному значению импульса, а в g раз завышенному. С учётом поправок на это завышение, все трековые данные будут говорить о сохранении именно классического импульса m V. Ибо релятивистский фактор g не будет присущ импульсу, как таковому, а будет являться следствием нелинейности шкалы в данной измерительной методике. Впрочем, можно до хрипоты спорить – так или этак интерпретировать трековые данные. Но мы обращаем внимание на бесспорный факт: вывод о релятивистском увеличении энергии частицы делается по результатам её взаимодействия только с полями – когда от этой чудовищной энергии никому «ни жарко, ни холодно». Давайте же использовать и другие методики измерения энергии частицы – по результатам её взаимодействия с веществом! Это будет прямое и честное измерение – если измерить всю энергию, в те или иные формы которой превратится энергия частицы! Здесь-то и находится «момент истины»: прямые и честные измерения показывают, что никакого релятивистского роста энергии не существует. Ну, действительно: кому удалось, из одного релятивистского электрона, извлечь, при его взаимодействии с веществом, энергию в несколько ГэВ? Или хотя бы в несколько МэВ? Давайте посмотрим! Вот, например, заряженные частицы оставляют треки в камере Вильсона или в пузырьковой камере. При образовании этих треков, превращения энергии, по меркам микромира, огромны – но они происходят, в основном, не за счёт энергии инициирующей частицы. Здесь регистрирующая среда пребывает в неустойчивом состоянии – это переохлаждённый пар или перегретая жидкость. Частица тратит кинетическую энергию лишь на создание ионов в среде – и эти потери энергии невелики. А ионы становятся центрами бурной конденсации или парообразования. Успей сфотографировать очаги фазовых превращений в среде – вот и трек частицы. Но энергия этих фазовых превращений – несоизмеримо больше ионизационных потерь частицы. А можно ли измерить сами ионизационные потери? Конечно, можно. В своё время в экспериментальной физике широко использовались замечательные приборчики: пропорциональные счётчики [Д2]. Влетев в этот приборчик, частица растрачивает свою кинетическую энергию на ионизацию атомов вещества-наполнителя – принципиально до полной своей остановки. Чем больше энергия частицы, тем больше ионов она создаёт, и тем больше генерируемый приборчиком импульс тока. Обращаем внимание: средняя энергия, требуемая для создания одной пары ионов, совсем невелика – это два-три десятка эВ [Э1]. По отношению к такой энергии, говорить о релятивистском завышении неуместно. Поэтому к показаниям пропорциональных счётчиков следовало бы относиться с большим доверием – поскольку имеются веские основания полагать, что они измеряют энергию частицы честно. И вот как выглядят результаты этих честных измерений. В «нерелятивистской области», пока энергия частиц малая, результаты её измерения пропорциональными счётчиками совпадают с результатами измерений по методике магнитного отклонения. Но в «релятивистской области» единство измерений нарушается: энергия, измеряемая по магнитной методике, лезет в релятивистскую бесконечность, а энергия, измеряемая пропорциональными счётчиками, выходит на насыщение и дальше не растёт [Д2]. Причём, не похоже на то, что счётчики «шалят»: все они – при разных типах и конструкциях – показывают одно и то же. А именно: никакого релятивистского роста энергии нет. Этот очевидный факт причинял релятивистам немало душевных страданий. Пришлось принимать меры: придумывать гипотезы, которые наукообразно разъясняли – отчего у пропорциональных счётчиков, при измерениях в релятивистской области, увеличиваются аппаратурные погрешности [Д2]. Да ведь как согласованно увеличиваются – в точности маскируя релятивистский рост, как будто его и нет вовсе! Знаете, дорогой читатель, физики обычно не упускают возможности позубоскалить над гипотезами ad hoc – так называются вспомогательные гипотезы, выдвинутые ради только какого-то одного трудно объяснимого случая. Так вот, для разных типов и конструкций пропорциональных счётчиков, «увеличение аппаратурных погрешностей» пришлось объяснять по-разному, так что гипотез ad hoc здесь набрался целый букет. И никто не зубоскалил. Все, похоже, понимали: грешно смеяться над больными. А страдать релятивистов заставляли не только пропорциональные счётчики. Была ещё одна методика прямого измерения тормозных потерь быстрых заряженных частиц – в фотоэмульсиях. Здесь частица тоже теряет энергию на ионизацию атомов, причём каждый образовавшийся ион становится центром формирования фотографического зёрнышка. И эти зёрнышки различимы под микроскопом. Значит, число ионизаций, произведённых частицей, можно пересчитать, а затем умножить это число на энергию одной ионизации – вот и получится исходная энергия частицы! И что же? А то, что и здесь всё получалось, как и в пропорциональных счётчиках. В «нерелятивистской области», число зёрнышек, умноженное на энергию одной ионизации, вполне соответствовало результатам «магнитной» методики. А в «релятивисткой области» число зёрнышек выходило на постоянную величину и дальше, практически, не росло [Б2]. И, опять же, использовались различные составы фотоэмульсий. И опять же, все они говорили одно и то же: если подходить к вопросу методом простого всматривания, то никакого релятивистского роста энергии не обнаруживается. И опять пришлось выдвигать гипотезы ad hoc. Насчёт того, что быстрая частица теряет энергию в фотоэмульсиях не только на ионизацию: есть, якобы, ещё и «недетектируемые» потери энергии – на возбуждение атомов или ядер, на выбивание нейтральных частиц, на излучение [Б2]. Пикантность ситуации в том, что эффективности разных каналов этих «недетектируемых потерь» по-разному зависят от энергии частицы – но в сумме эти потери, якобы, так согласованно нарастают, что в точности маскируют ожидаемый релятивистский рост детектируемых потерь! Не проще и не разумнее ли допустить, что, в релятивистской области, потери не растут просто потому, что истинная кинетическая энергия частицы имеет верхний предел? Нет, этот вопрос не решается по критериям простоты и разумности. Тут дело на принцип пошло! И, чтобы релятивистам не утруждать себя каждый раз объяснениями того, куда же деваются релятивистские излишки энергии частицы, они пустились на небывалый в истории физики прецедент. «Магнитная методика, - заявили они, - непогрешима! Поэтому все остальные методики измерения энергии следует калибровать именно по ней, по магнитной!» После этого им, действительно, полегче стало. Кстати, были ведь эксперименты, где «магнитная» и «немагнитная» методики встречались, так сказать, нос к носу. Это получалось там, где измеряли импульс отдачи у атома, из ядра которого выстреливался релятивистский электрон при бета-распаде. Здесь устраивалась «очная ставка» двум методикам: импульс отдачи атома измерялся по «немагнитной» методике, а импульс выстреливаемого электрона – по «магнитной», во всей её непогрешимой красе. Первые же опыты такого рода [К5] поставили в крайне затруднительное положение учёных, стоявших на позициях закона сохранения релятивистского импульса. Ведь импульс электрона получался чудовищно больше, чем импульс отдачи атома. Следите за логикой: импульс электрона измерялся по непогрешимой методике – значит, правильно измерялся именно он. Следовательно, импульс отдачи у атома оказывался чудовищно меньше, чем требовалось по закону сохранения релятивистского импульса. Т.е., подавляющая часть импульса отдачи куда-то тихо исчезала. Экспериментаторы клялись и божились, что это не их рук дело – а теоретики не могли в это поверить... «Пялились исследователи на фотопластинки, вертели ими так и сяк… Можно было поступить совсем просто: отбросить иллюзорные релятивистские завышения импульсов у электронов, и тогда их результирующие импульсы становились бы равными импульсам отдачи! Но – что вы! это было бы святотатство! Уж лучше было сидеть и страдать молча… Ферми смотрел-смотрел на эти страдания, и его доброе сердце дрогнуло. «Ладно, - подмигнул он, - вы только не плачьте! Вот что мы сделаем: введём новую частицу. И припишем ей всё, что требуется. Вам нужен импульс? – у ней он есть!» - «Как?! – просияли от радости экспериментаторы. – Так просто? Впрочем, погодите-погодите. Мы же такую возможность исследовали. Никаких следов третьей частицы при бета-распаде не обнаруживается!» - «Ну, и что такого? Если следов не обнаруживается, значит, эта частица их не оставляет! Я же говорю – припишем всё, что требуется!» - «Да, но… странно как-то. Трудно поверить! Частица… импульс имеет… и – никаких следов… Как же её поймать?» - «А зачем обязательно – поймать? Сам по себе процесс ловли – разве он удовольствия не доставляет? Так ловите, до скончания века, и наслаждайтесь! На зависть окружающим!» - «А, ведь, действительно! Позвольте полюбопытствовать, а как предлагается назвать эту неуловимую прелесть?» - «Да придумаем хохмочку какую-нибудь… Вот: назовём эту прелесть нейтрончиком!» [Д4] Уж простите за приведённую цитаточку, но так и было: нейтрино «открыли» только для того, чтобы не рухнул закон сохранения релятивистского импульса. А чтобы успокоить тех, кто сомневался в реальности нейтрино, ей быстренько приписали статус одной из фундаментальных, абсолютно стабильных, частиц – которых, как считается, всего-то четыре. В физике организовали новый раздел – «Физика нейтрино». Понастроили грандиозных «детекторов». Мне довелось побывать на одном из них – в Баксанском ущелье на Кавказе. Чтобы только нейтрино, с их выдающимися проникающими способностями, могли долетать до этого «детектора», помещение для него выдолблено в центре подошвы огромной каменной горы: эта гора прикрывает «детектор» сверху... Так, думаете, эти детекторы реагируют на нейтрино? Да нет, они реагируют на продукты реакций, которые, как полагают теоретики, могут порождать только нейтрино – да и то крайне редко. Уж больно оно неуловимое. Кстати, по свойству исключительно слабо взаимодействовать с веществом, нейтрино резко отличается от остальных частиц, испускаемых при радиоактивных превращениях: нейтрино «умирает» на много порядков реже, чем рождается. Налицо абсурдная асимметрия, которая до сих пор не имеет объяснения. Не проще ли устранить эту асимметрию, признав, что нейтрино и релятивистский импульс являются теоретическими иллюзиями? Но нам могли бы ещё возразить: если релятивистские излишки энергии были бы иллюзиями, то это непременно проявилось бы при сопоставлении энергии частиц с энергиями гамма-квантов, которые измеряются независимыми способами. Увы – хотя арсенал способов измерения энергии гамма-квантов довольно-таки богат [Э2], об их независимости не может быть и речи. Целый ряд методов основан на измерениях энергий конверсионных электронов и вторичных электронов, которые выстреливаются в результате комптон-эффекта, фотоэффекта, и образования электрон-позитронных пар – но «магнитный анализ спектров вторичных электронов… является наилучшим методом точного измерения энергии g-квантов» [Э2]. По результатам этого знакомого «наилучшего метода» калибруются остальные методы – в которых определяются пороги ядерных реакций или энергии вторичных ядерных частиц, а также такой, казалось бы, обособленный метод, как измерение длины волны гамма-излучения с помощью дифракции на кристалле [М1]. Этот метод сохраняет свою обособленность, опять же, лишь при малых энергиях гамма-квантов. Но, уже при энергиях ~100 кэВ, соответствующая длина волны гамма-излучения на порядок меньше, чем расстояния между атомными плоскостями в кристаллах, что весьма затрудняет – особенно при скользящих углах падения – определение индекса брэгговской дифракции; так что калибровка здесь необходима. Выходит следующее: если, как мы полагаем, метод магнитного отклонения даёт не истинную, а релятивистски завышенную энергию, то с аналогичным завышением определяются и энергии гамма-квантов! Кстати, специалистам по гамма-спектроскопии хорошо известен вопиющий факт, имеющий место при аннигиляции быстрых электронов и позитронов. Казалось бы: чем больше энергии электронов и позитронов, тем больше должна быть энергия продуктов их аннигиляции. Ничего подобного! Даже когда исходные частицы являются релятивистскими, их аннигиляция даёт узкополосное характеристическое гамма-излучение с энергией 511 кэВ [Д1]. Именно поэтому излучение аннигиляции обеспечивает важнейшую калибровку в гамма-спектроскопии [Д2]! Заметим, что в измерениях по магнитной методике можно было бы до некоторой степени избегать иллюзорных завышений, если использовать частицы с достаточно большой массой – поскольку энергия, которая, согласно (1.5.2), близка к предельной у электрона, далека от предела у протона. Отсюда, кстати, вытекает возможность получения ещё одного свидетельства о наличии ограничения у кинетической энергии частицы. Известно множество ядерных реакций с порогами всего в несколько МэВ [Б2]. Эти реакции инициируются, например, протонами, для которых энергия в несколько МэВ является ничтожной, и есть гарантия, что пороги при этом измеряются без релятивистского завышения. Эти же реакции инициируются и нейтронами, и гамма-квантами – была бы их энергия выше пороговой. Электроны, которые имели бы энергию в несколько МэВ, инициировали бы эти реакции, казалось бы, ещё охотнее, чем протоны – ведь электроны притягиваются к ядру, а не отталкиваются от него. Но нет: что-то мешает электронам инициировать ядерные реакции. Считается, что релятивистские электроны, при взаимодействии с ядрами, испытывают почему-то лишь упругое рассеяние [К4]. Налицо странная асимметрия: вылететь из ядра, прихватив оттуда немалую энергию, электрон может (при бета-распаде) – а ударить по ядру, сообщив ему такую же энергию, электрон не может! Что по этому поводу говорит физика высоких энергий? А она по этому поводу хранит гробовое молчание. Высокие энергии оказалось гораздо практичнее измерять не по электронной, а по протонной шкале. Тут уж не до единства измерений – быть бы живу! Ибо из опыта ясно, что, скажем, 3 МэВа у протона – это полноценные 3 МэВа, а 3 МэВа у электрона – это пустышка. Но как же так? Неужели не проводились эксперименты по прямому измерению энергии быстрых электронов – калориметрическим методом – при известном ускоряющем вольтаже? Ведь было сооружено множество ускорителей. И нас уверяют, что без релятивистского роста энергии у быстрых частиц, ни один ускоритель не работал бы! Так покажите нам его, прямо измеренный релятивистский рост! Где же изобилие публикаций на эту тему? В это трудно поверить, но на эту тему известна всего одна (!) публикация – о которой релятивисты если и упоминают, то делают это как-то странненько, сквозь зубы. В чём же был секрет у Бертоцци [Б3], если только он один и смог прямо измерить релятивистский рост? Бертоцци использовал двухступенчатую схему ускорения электронных сгустков. На первой ступени электроны ускорялись статическим электрическим полем, формируемым с помощью высоковольтного генератора Ван-де-Граафа. А второй ступенью был линейный индукционный ускоритель. При известном ускоряющем вольтаже, автор измерял две величины – скорость и энергию электронов. Скорость он определял пролётно-импульсным методом: по времени, разделявшему два всплеска тока, которые наводились пролетающим сгустком в электродах, разнесённых на известное расстояние. А об энергии электронов автор судил по нагреву алюминиевого стаканчика, который улавливал разогнанные электронные сгустки. Если релятивистский рост энергии имеет место, то, при изменении ускоряющего вольтажа, скорость электронов должна была, практически, не изменяться (будучи близкой к скорости света), а их энергия должна была изменяться весьма заметно. На первый взгляд, именно такую зависимость и демонстрируют пять экспериментальных точек, представленных автором на графике. Но не всё было так просто. В таблице (см. ниже) первые два столбца отображают ускоряющий вольтаж и отношение измеренной скорости электронов к скорости света. Но вот, внимание: «При вольтажах 0.5, 1.0 и 1.5 МэВ линейный ускоритель не был включён» (перевод наш) – эту особенность отражает третий столбец в таблице. И, наконец: «Измерения энергии проводились для ускоряющих вольтажей 1.5 и 4.5 МэВ» (перевод наш) – эту особенность отражает последний столбец в таблице.
Таким образом, реальных экспериментальных точек оказывается, вместо пяти, всего две, причём одна из них была получена, когда индукционный ускоритель был выключен, а другая – когда он был включён. В этом – и секрет фокуса. Когда индукционный ускоритель работает, он индуцирует вихревые токи в металлических штучках. Его самого приходится охлаждать проточной водой! Конечно, вихревые токи наводились и в мишени-стаканчике – вот и грелся стаканчик сильнее. Эту мелочь автор почему-то не учёл, и соответствующей калибровки не проделал. Каким образом у него две точки удачно легли на релятивистскую кривую – это уже не имеет значения: совершенно очевидно, что дело здесь не в релятивистском росте. Тогда становится понятно, почему никто из коллег Бертоцци не отважился подтвердить его эксклюзивный результат. А ведь могли бы и на кольцевых циклических ускорителях мишеньки погреть – хотя бы между делом! Релятивистский рост энергии стоит того! Да могли бы вкачать в электроны не какие-то жалкие МэВы, а те самые ГэВы, о которых домохозяйкам все уши прожужжали! Так нет же. Эх, знали бы домохозяйки, что каждый удачный прогон на серьёзном ускорителе – это для релятивистов чудо, которого они до сих пор понять не могут. Надо же: вкачивают-вкачивают сумасшедшую энергию в ускоряемые электроны, потом этими электронами бьют по мишени… а там, вместо сумасшедшей энергии, выделяется смехотворный пшик! Вот в этом и заключается «работа» ускорителей! На такие слова релятивисты вытаскивают ещё один аргумент: им, оказывается, хорошо известно о том, что релятивистский прирост энергии может превратиться в частицы вещества, которых до этого не было. Представляете – речь не просто о подтверждении наличия релятивистского роста, речь о нечто большем: о том, что из кинетической энергии можно лепить новое вещество! Если бы это было так – грош цена была бы нашей логике «цифрового» мира. Но, посмотрим, какие же подтверждения своих слов предъявляют релятивисты. А вот, например, они говорят про каскадные ливни [Я1] в атмосфере, порождаемые протонами космических лучей с высокой энергией. Традиционно считается, что электроны и позитроны в каскадных ливнях рождаются за счёт убыли кинетической энергии инициирующего протона. Оценки этой энергии по числу треков в сильных ливнях дают величины, на много порядков превышающие энергию покоя протона. Но ведь нет доказательств того, что все эти электроны и позитроны «рождаются» из кинетической энергии протона. На наш взгляд, более разумна версия о том, что протон тратит кинетическую энергию лишь на освобождение пар электрон-позитрон, находившихся в предельно связанном состоянии [Г1], причём, подавляющее большинство треков в ливне оставляют электроны и позитроны вторичные, третичные, и т.д. – на появление которых энергия протона не тратится совсем. Нам здесь легко «спекулировать на трудностях», потому что этот аргумент с релятивистскими протонами природного происхождения – неубедителен. Зато на протонных ускорителях, как уверяют нас, вещество рождается из кинетической энергии полностью контролируемым образом! И рассказывают про нашумевшую в своё время историю с открытием антипротона [Ч1]. В 1955 г. на про
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.44.46 (0.033 с.) |

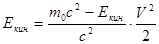 , (1.5.1)
, (1.5.1)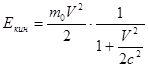 . (1.5.2)
. (1.5.2)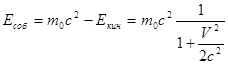 . (1.5.3)
. (1.5.3)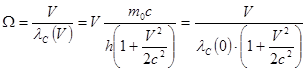 . (1.5.4)
. (1.5.4)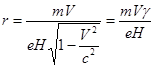 , (1.6.1)
, (1.6.1)


