
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действие тяготения на свободный квантовый пульсатор.
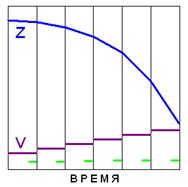
Хорошо известно, что пробное тело, которому не мешает падать опора или подвес, приобретает ускорение свободного падения. По логике вышеизложенного (3.11), это происходит потому, что, у каждой частицы тела, управляющая ей программа периодически производит приращения вектора скорости – значения и направления этих приращений должны быть в полном соответствии с локальным вектором ускорения свободного падения. Этот вектор определяется локальным градиентом частот (3.7.3), и, значит, для расчёта правильных приращений вектора скорости частицы, управляющая программа должна располагать информацией о значении и направлении этого градиента. Чтобы получить эту информацию, требуется узнать параметры локального участка частотного склона (3.7). Значит, для точек в окружающей частицу области координатного поля, требуется выполнить считку предписанных значений частот квантовых пульсаций (для свободного и покоящегося квантового пульсатора). Эта считка, как можно допустить, производится последовательно: сначала для ближайших к частице точек координатного поля, затем для точек следующего шарового слоя, и так далее – т.е. считка производится на фронте расходящейся от частицы сферической волны, поэтому эту программную процедуру мы называем термином «гравитационное сканирование». Скорость распространения волны гравитационного сканирования – которая является чисто программной реальностью! – определяется, по логике «цифрового» физического мира, быстротой программного сканирования координатного поля, и её значение равно скорости света в вакууме. Каждый прогон гравитационного сканирования заканчивается на таком радиусе от частицы, чтобы, в пределах просканированной сферической области, уверенно проявилось направление максимального перепада частот, задающее местную вертикаль (3.7). При этом, величина максимального перепада частот, отнесённая к диаметру просканированной области, даст величину искомого градиента частот. Таким образом, приобретается вся информация, необходимая для расчёта очередного приращения к вектору скорости частицы – и, сразу после каждого прогона гравитационного сканирования, это рассчитанное приращение производится. При свободном падении частицы, происходящем по вышеописанному алгоритму, ускорение свободного падения приобретается ей принципиально не так, как это обычно полагают. А именно, вектор скорости частицы изменяется НЕ непрерывно, а дискретными мгновенными скачками, на интервалах времени между которыми вектор скорости остаётся постоянным – иллюзия же его непрерывного изменения является результатом сглаживания при наблюдении этого процесса. На Рис.3.12.1 схематически показаны зависимости от времени у скорости V и вертикальной координаты Z при свободном вертикальном падении на малом перепаде высоты, где ускорение свободного падения можно считать постоянным – зелёными отрезками обозначены интервалы времени, на которых производится гравитационное сканирование. Как можно видеть, зависимость скорости от времени имеет ступенчатый характер, а зависимость вертикальной координаты от времени представляет собой кусочно-ломаную, которая превращается в параболу при сглаживании.
Рис.3.12.1
Заметим, что «ступенька» вертикального приращения скорости dV и интервал времени t g, которым разделены две соседние «ступеньки», должны подчиняться очевидному соотношению dV/t g =g, где g - величина локального ускорения свободного падения. Но, в условиях малых и больших g, параметры гравитационного сканирования должны различаться. Наиболее логичным нам представляется вариант, при котором периодичность гравитационного сканирования, т.е. интервал времени t g, не изменяется, и тогда радиус гравитационного сканирования в условиях малых g больше, чем в условиях больших g – для обнаружения того перепада частот, который достаточен для уверенных расчётов (см. выше). Сделаем некоторые оценки для параметров гравитационного сканирования, взяв в качестве базового значения g его значение на поверхности Земли, т.е. 9.8 м/с2. Начнём с оценки для величины dV×t g,т.е. для произведениядискрета приращения вертикальной скорости на период повторения этих приращений – эта величина равна вертикальному смещению на первом отрезке вертикального свободного падения после устранения действия опоры или подвеса; на этом отрезке, постоянная скорость падения равна dV. С одной стороны, если дискретные эффекты при свободном падении (Рис.3.12.1) напрямую не проявляются, то величина dV×t g едва ли больше, чем характерный размер атома. С другой стороны, этой величине бессмысленно быть много меньше, чем характерный размер атома – поскольку, в таком случае, был бы совершенно неоправданно увеличен объём производимых программных манипуляций. Поэтому будем исходить из того, что величина dV×t g на порядок меньше характерного размера атома и составляет 10-11 м. Комбинируя соотношения dV×t g =10-11 м и dV/t g =9.8 м/с2, мы находим, что t g»10-6 с, т.е. приращения вертикальной скорости частицы производятся на частоте»1 МГц. Эта цифра представляется нам реалистичной, поскольку частота в 1 МГц много меньше частот циклических процессов, характерных как для химических связей (8.3), так и для смен валентных конфигураций, дающих переключения химических связей (8.6) – т.е. дискретность действия тяготения на частицы тела не является фактором, который серьёзно вмешивался бы в процессы, поддерживающие микроструктуру тела. Приведём ещё одну показательную цифру: при движении со скоростью 7.9 км/с – это первая космическая скорость вблизи поверхности Земли – частица за время t g»10-6 с пролетает около 8 мм. Тогда, согласно излагаемому подходу, траектория частицы при свободном облёте Земли представляет собой не окружность, а кусочно-ломаную – из прямолинейных отрезков по 8 мм. При этом, величина дискретных вертикальных приращений скорости составляет, как и при вертикальном свободном падении, произведение g×t g, т.е.»10-5 м/с.
Теперь скажем о радиусах гравитационного сканирования на разных удалениях от Земли. Если считать, что на границе области действия земного тяготения – т.е. на удалении от центра Земли примерно в 900 тыс. км – каждый прогон гравитационного сканирования длится весь промежуток времени t g =10-6 с, то радиус гравитационного сканирования, выполняемого со скоростью света (см. выше), должен составлять там 300 метров. При ускорении свободного падения, равном там около 5×10-4 м/с2, обнаруживаемый перепад частот на перепаде высот в 600 м должен, согласно (3.7.3), в относительном исчислении составлять D f / f»3.3×10-18. Вблизи поверхности Земли, такой же перепад частот обнаруживался бы при радиусе гравитационного сканирования всего в 1.5 см. Подчеркнём, что все вышеприведённые параметры гравитационного сканирования являются грубыми оценками и имеют исключительно ориентировочный характер. Теперь рассмотрим вопрос о превращениях энергии при свободном падении квантового пульсатора. Согласно концепции «цифрового» физического мира, никакой «потенциальной энергией в поле тяготения» квантовый пульсатор не обладает – потенциальная энергия является фикцией, поскольку ей не соответствует никакая форма движения (1.3). Согласно принципу автономных превращений энергии (1.5), кинетическая энергия у частицы появляется за счёт такой же убыли её собственной энергии, т.е. за счёт убыли её массы (1.4) – и процесс свободного падения не является исключением из этого правила. Но при свободном падении масса изменяется, по мере изменения высоты, ещё и из-за действия программных предписаний, формирующих частотный склон (3.7). Так, при свободном полёте вниз, масса покоя уменьшается, и кинетическая энергия растёт за счёт уменьшения и без того уменьшающейся собственной энергии.
Действительно, на частотном склоне зависимость энергии свободного квантового пульсатора от его расстояния r до центра частотной воронки есть
где m 0 - масса покоя «на бесконечности», а, практически, на границе данной частотной воронки; GM - в терминах традиционного подхода, гравитационный параметр «силового центра», т.е. произведение гравитационной постоянной на его массу. Индекс «полн» у энергии (3.12.1) означает, что она является полной энергией квантового пульсатора – которая, при появлении у него кинетической энергии, распадается на сумму двух его энергий: собственной и кинетической. Исходя из выражения (3.12.1), и с учётом принципа автономных превращений энергии (1.5), для кинетической энергии того же квантового пульсатора можно записать:
где V - его локально-абсолютная скорость (2.3). Комбинируя (3.12.1) и (3.12.2), для собственной энергии квантового пульсатора получаем:
Выражения (3.12.2) и (3.12.3) показывают, что масса квантового пульсатора, покоящегося или движущегося на частотном склоне, есть
умножение этой массы на c 2 даёт собственную энергию квантового пульсатора, как функцию от r и V. Сказанное схематически иллюстрирует Рис.3.12.2, где кривая АС показывает зависимость, от r, у собственной энергии покоящегося квантового пульсатора, а кривая АВ – то же, для случая свободного вертикального падения с радиуса r 1 на радиус r2, с нулевой начальной скоростью. По логике вышеизложенного, кинетическая энергия, приобретённая при прохождении этого перепада высот, равна длине отрезка ВС, а уменьшение собственной энергии покоя из-за действия частотного склона равно, для того же перепада высот, длине отрезка DC. Прежде чем дать ответ на ключевой вопрос – как соотносятся между собой отрезки ВС и DC, обратим внимание на следующее. Не противоречит ли наш подход закону сохранения энергии? – ведь, согласно этому подходу, при свободном полёте с изменением высоты полная энергия свободного квантового пульсатора не остаётся постоянной – это отражает кривая АС! Действительно, по логике проявления частотного склона, часть
Рис.3.12.2
собственной энергии квантового пульсатора, по мере его перемещения вниз, «изымается из оборота» и исчезает из физического мира. Но мы не усматриваем здесь грубого противоречия с законом сохранения энергии. Действительно: во-первых, изъятие мизерной части собственной энергии из оборота происходит строго контролируемым образом, поскольку оно обусловлено работой соответствующих программ. Во-вторых, это изъятие полностью обратимо: при перемещении квантового пульсатора вверх, программы увеличивают его собственную энергию, добавляя энергию в физический мир. Таким образом, для записи корректного баланса энергий квантового пульсатора при его перемещениях по высоте, следует учитывать вклад DC из-за проявления частотного склона. Этот вклад мы будем называть гравитационной поправкой D E g – её величина, очевидно, есть
Теперь ответим на вопрос: как, при вертикальном свободном падении, соотносятся гравитационная поправка D E g и приобретаемая кинетическая энергия? В нерелятивистском приближении, выражение для кинетической энергии (3.12.2) приобретает хорошо знакомый вид: Eкин = m 0 V 2/2. При начальной скорости V 1, после прохождения малого перепада высот D r, на котором ускорение свободного падения g можно считать постоянным, справедливо соотношение
и тогда
Поскольку, для малого перепада высот, гравитационная поправка (3.12.5) тоже равна m 0 g D r, то, на малом перепаде высот, прирост кинетической энергии при свободном падении равен гравитационной поправке. Это означает, что, для любого r, крутизна у кривой АВ в два раза больше, чем у кривой АС, и – в сделанных выше приближениях – равенство между приростом кинетической энергии и гравитационной поправкой остаётся справедливо и для больших перепадов высот. Отсюда немедленно следует соотношение
справедливость которого для свободных полётов по кеплеровым траекториям не вызывает сомнений [Л4]. Следует подчеркнуть, что вышеописанное действие тяготения на частицу представляет собой в чистом виде безопорную тягу. Здесь приобретение частицей ускорения не сопровождается динамической реакцией ни у какого из физических объектов: третий закон Ньютона хорошо работает для соударений тел, для реактивного движения – но отнюдь не для ускорения свободного падения, вызываемого прямыми программными воздействиями. Добавим, что выше мы говорили о ситуации, при которой гравитационное сканирование для частицы вещества проводится по пространству, свободному от других частиц. При наличии же достаточного количества окружающих частиц, градиенты частот могут выявляться проще – через считку собственных энергий окружающих частиц. Причём, такое сканирование даже имеет приоритет перед сканированием «пустого» координатного поля. Это означает, что если в теле создан (неважно, каким способом!) градиент собственных энергий у частиц, то частицы тела будут испытывать силовое воздействие – с ускорением безопорной тяги, определяемым этим градиентом аналогично (3.7.3). Проиллюстрируем это на примере центробежных сил, действующих на элементы вращающегося диска. Как следует из (1.5.3), собственная энергия частицы диска составляет
где m 0 – масса этой частицы диска при отсутствии его вращения, w - угловая скорость вращения, R - радиус вращения. Тогда, для ускорения безопорной тяги, по аналогии с выражением (3.7.3) получаем:
т.е. хорошо известную величину центробежного ускорения. Отсюда мы делаем вывод, что центробежные силы – которые вполне реальны, поскольку они реально растягивают диск в радиальных направлениях – эти силы обусловлены радиальными градиентами собственных энергий у частиц вращающегося диска.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.151.214 (0.017 с.) |
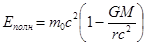 , (3.12.1)
, (3.12.1)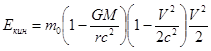 , (3.12.2)
, (3.12.2)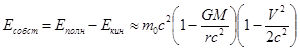 . (3.12.3)
. (3.12.3)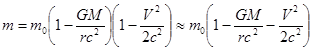 (3.12.4)
(3.12.4)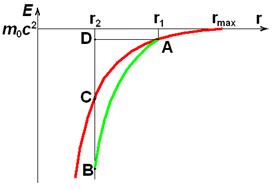
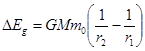 . (3.12.5)
. (3.12.5)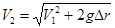 , (3.12.6)
, (3.12.6)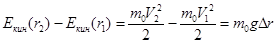 . (3.12.7)
. (3.12.7)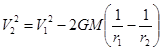 , (3.12.8)
, (3.12.8)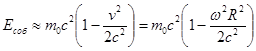 , (3.12.9)
, (3.12.9)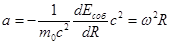 , (3.12.10)
, (3.12.10)


