
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные склоны. Ускорение свободного падения.
Выше мы привели ряд примеров, которые свидетельствуют о том, что вещество не обладает способностью порождать тяготение. Оно не притягивает, оно лишь подчиняется тяготению. К чему же оно тяготеет? В такой форме – «К чему?» - вопрос некорректен. Правильнее спросить: «Куда направлено тяготение?» Тогда ответ таков: «Оно направлено вниз по местной вертикали». А эти местные вертикали формируются следующим образом. Как отмечалось выше (1.4), частоты квантовых пульсаций заданы программно. Если частота квантовых пульсаций, например, электрона, была бы задана одинаковой во всём пространстве, то в таком мире не было бы физических проявлений выделенных направлений – местных вертикалей. Чтобы создать эти выделенные направления, программы обязывают частоты квантовых пульсаторов зависеть от местоположения в координатном поле (2.3). Таким образом формируется программная реальность, которую мы называем частотными склонами. Это просто совокупность программных предписаний, расклад частот квантовых пульсаций по координатам: частица, оказавшаяся в таком-то месте координатного поля, должна иметь такую-то частоту квантовых пульсаций, а, оказавшись в другом месте – соответственно, другую частоту квантовых пульсаций (такой же расклад получается и для массы частицы (1.4)). Например, в околоземном пространстве, частота f квантовых пульсаций электрона – и, соответственно, его масса – увеличивается при увеличении его расстояния r от центра Земли:
где f 0 - частота «на бесконечности», а, практически, на границе земного координатного поля, GM З – в терминах традиционного подхода, гравитационный параметр Земли, т.е. произведение её массы на гравитационную постоянную, c - скорость света. Таким образом, направление «вниз» по местной вертикали – это направление, в котором предписанные частоты квантовых пульсаций уменьшаются быстрее всего. Крутизна частотного склона на поверхности Земли была впервые измерена, с помощью мёссбауэровской спектроскопии, в 1959 г. Паундом и Ребкой [П2]. Правда, они неверно интерпретировали свой результат – полагая, что измерили «гравитационное красное смещение», т.е. гравитационный сдвиг частоты у гамма-квантов, движущихся вертикально. Они не приняли во внимание, что если источник и поглотитель находятся на разных высотах, то их спектральные линии имеют такой же взаимный гравитационный сдвиг [Л3]. Если ещё и гамма-кванты, при своём вертикальном движении, изменяли бы свою частоту, то итоговый эффект был бы удвоенный – а он был одинарный. Строго говоря, схема эксперимента Паунда и Ребки не позволяла сделать вывод о причине обнаруженного эффекта: является ли он следствием взаимного сдвига линий источника и поглотителя, или следствием сдвига частоты гамма-квантов, движущихся по вертикали. Но в дальнейшем был проведен целый ряд экспериментов с транспортируемыми атомными часами, в частности, многочисленные применения этих часов на бортах ИСЗ. Эти эксперименты убеждают нас в том, что гравитационные сдвиги квантовых уровней энергии в веществе непременно имеют место – причём, они в точности объясняют и результат Паунда и Ребки. Значит, эти авторы измерили не сдвиг частоты у гамма-квантов, а именно крутизну частотного склона на поверхности Земли. Вот параметры этой крутизны: при 22.5-метровой разнице высот расположения мёссбауэровских источника и поглотителя, относительная разность частот составила около 2.5×10-15 [П2].
Учёт реальности частотных склонов даёт простое и естественное объяснение такого феномена, как гравитационное изменение хода атомных часов. Этот феномен проявляется тем, что атомные часы, находящиеся выше, идут несколько быстрее, чем такие же атомные часы, находящиеся ниже. Как следует из (3.7.1), при небольшом перепаде высот D h, на котором ускорение свободного падения g можно считать постоянным, гравитационная относительная разность частот одного и того же квантового перехода составляет
Этот феномен, как показывает опыт (2.10), отнюдь не является следствием т.н. гравитационного замедления времени вблизи массивных тел. Концепция гравитационного замедления времени является спекуляцией, причём спекуляцией совершенно излишней, если реальностью является прямое программное управление частотами квантовых пульсаций, порождаемое частотными склонами. Как отмечалось выше (2.8), энергия связи частиц является характеристической величиной для конкретной структуры, составляя определённый процент от собственных энергий связанных частиц. Значит, если собственные энергии частиц изменяются из-за предписаний частотного склона аналогично (3.7.2), то так же изменяется и энергия связи частиц – а, значит, и соответствующие квантовые уровни энергии сдвигаются так, что разности между ними испытывают такие же изменения. Вот почему энергии и частоты квантовых переходов зависят от гравитационного потенциала – что, на практике, проявляется как зависимость от высоты.
Ещё одним атрибутом частотного склона является то, что для любой локальной области координатного поля, в которой он действует, соответствующим градиентом частот квантовых пульсаций определяется вектор ускорения свободного падения – которое приобретает тело, если ему не мешает падать опора или подвес. Выражение для вектора ускорения свободного падения имеет вид [Г5]:
где d/ d r – градиент (вектор), c – скорость света. Как можно видеть, вектор g противоположен градиенту частот, т.е. он направлен вертикально вниз. О чём говорит выражение (3.7.3)? Прежде всего, оно подчёркивает непричастность масс к порождению тяготения, поскольку, как можно видеть, ускорение свободного падения не зависит от массы «силового притягивающего центра»: оно определяется лишь геометрией локального участка частотного склона. Далее, из выражения (3.7.3) тривиально следует объяснение того факта, что, скажем, в одном и том же месте области действия тяготения Земли, различные тела имеют одно и то же ускорение свободного падения – независимо от их массы, формы, химического состава и агрегатного состояния. Эйнштейн придавал этому факту фундаментальное значение. Он полагал, что его теория объяснила этот фундаментальный факт. Там вышло вот что: в ньютоновском законе всемирного тяготения фигурирует т.н. гравитационная масса тела, а в выражении второго закона Ньютона – его инертная масса. Комбинация этих выражений даёт, что ускорение свободного падения тела прямо пропорционально отношению его гравитационной массы к инертной. А это отношение в каждом месте одинаково для различных малых тел – и пусть оно, мол, равно единице! Тогда, мол, всё сходится! Но у этого «объяснения» есть всего один недостаточек. Оно, может, и работало бы, если понятие «гравитационная масса» имело бы физический смысл – если массы обладали бы притягивающим действием. Но, как проиллюстрировано выше, это не так. А одинаковость ускорения свободного падения у разных тел обусловлена тем, что в любом месте крутизна частотного склона, порождающего тяготение, одинакова для всех. Поэтому, когда говорят, что эксперименты Этвёша, Дикке и Брагинского установили равенство инертной и гравитационной масс с точностью аж до двенадцатого знака, то надо понимать, что установили-то, с этой точностью, одинаковость ускорений свободного падения для различных тел, и ничего сверх этого. Согласно (3.7.3), идентичность этих ускорений, сообщаемых разным малым телам одним и тем же участком частотного склона – это по определению так. Не нужно здесь изображать заумную «фундаментальность»!
Наконец, легко убедиться в том, что выражение (3.7.3) вполне согласуется с результатом вышеупомянутого эксперимента Паунда и Ребки: измеренная ими относительная разность частот, делённая на соответствующий перепад высоты и умноженная, согласно (3.7.3), на квадрат скорости света, даёт величину ускорения свободного падения на поверхности Земли.
Планетарные частотные воронки. Унитарное действие тяготения. Совокупность окружающих планету частотных склонов представляет собой сферически-симметричную частотную воронку. При зависимости частот квантовых пульсаций от расстояния до центра планеты по типу (3.7.1) – вплоть до границ планетарного координатного поля – величина ускорения свободного падения (3.7.3) обратно пропорциональна квадрату расстояния до центра планеты. В чём смысл такой программной реальности, как планетарная частотная воронка? Выше мы говорили о том, что солнечное и планетарные координатные поля разграничены и не перекрываются (2.2), что частотные склоны созданы с привязкой к координатным полям (3.7), и что вектор ускорения свободного падения определяется локальными параметрами частотного склона (3.7). Сопоставляя всё это, мы приходим к тому, что область планетарного координатного поля, область планетарной частотной воронки и область действия планетарного тяготения – это одна и та же область пространства в физическом мире. Таким образом, в вопросе о тяготении мы приходим к самому поразительному несогласию между официальной теорией и реальностью – между законом всемирного тяготения и организацией действия тяготения в «цифровом» физическом мире. Согласно закону всемирного тяготения, притягивающее действие каждой массочки простирается, практически, до бесконечности, и тяготение, порождаемое разными массочками, действует аддитивно – например, в любом месте Солнечной системы, на пробное тело суммарно действует тяготение всех больших тел Солнечной системы. В реальности же всё совсем по-другому: области действия тяготения больших тел Солнечной системы строго разграничены, и тяготение действует не по аддитивному принципу, а по унитарному – на пробное тело действует только одно тяготение, определяемое локальными параметрами той области тяготения, в которой тело находится. То есть, в пределах каждой планетарной частотной воронки действует только планетарное тяготение, а солнечное тяготение там «отключено», а в межпланетном пространстве, не занятом частотными воронками планет, действует только солнечное тяготение. Главным свидетельством о такой разграниченности областей действия тяготения является скачкообразное изменение типа кеплеровой траектории космического аппарата на определённом расстоянии от планеты (2.6) – при пересечении аппаратом границы области планетарного тяготения.
Заметим, что даже если солнечное тяготение действовало бы и в пределах планетарных частотных воронок, складываясь там с планетарным тяготением, то такое совместное действие не могло бы обеспечить центростремительного ускорения планет к Солнцу. По аналогии с изложенным в 3.4, участок солнечный склона, приходящийся на планетарную воронку, деформировал бы её – отчего возникало бы направленное к Солнцу воздействие на вещество планеты. Но ведь планета продолжала бы оставаться в деформированной воронке. Значит, если даже солнечный склон навёл бы «перекос» этой воронки, планета всего лишь заняла бы в ней новое положение равновесия – но центростремительного ускорения к Солнцу планета не имела бы, если его не имела бы сама планетарная частотная воронка [Г4]. А это уже очень интересно. Это приоткрывает тайну происхождения Солнечной системы. Ни одна из выдвинутых на эту тему научных гипотез, основанных на законе всемирного тяготения, не проясняет главного: каким это дивным образом планеты в своё время приобретали «правильные» векторы скорости, чтобы продолжать своё движение по, практически, круговым орбитам, радиусы которых зависят от их порядкового номера, подчиняясь эмпирическому правилу Тициуса-Боде [С3]. Мы же, с учетом вышеизложенного, приходим к выводу об искусственном устроении движения планет. Вещество планет просто удерживается в центрах планетарных частотных воронок – для которых организовано орбитальное движение вокруг Солнца. Организовано, конечно, чисто программными средствами [Г4] – да так, чтобы для ускорений планетарных частотных воронок к Солнцу и друг к другу имитировался закон обратных квадратов (см. также 6.10)! И, в дополнение к этому чуду, имеются экспериментальные свидетельства о том, что в пределах планетарных частотных воронок, т.е. в областях действия планетарного тяготения, солнечное тяготение действительно «отключено», т.е. планетарная частотная воронка не деформирована из-за наложения на неё соответствующего участка солнечного частотного склона. Так, убийственное свидетельство об «отключенности» солнечного тяготения в окрестностях Земли появилось с началом эры GPS. Если бы солнечное тяготение действовало здесь аддитивно с земным, то спутники GPS, движущиеся над дневной и ночной сторонами Земли, находились бы в неодинаковых гравитационных потенциалах. Соответственно, бортовые атомные часы на этих спутниках имели бы неодинаковые хода. Максимальная относительная разность этих ходов 2 a S R / c 2, где a S - ускорение свободного падения к Солнцу на радиусе орбиты Земли, R - радиус орбиты спутников GPS, c - скорость света, составляла бы величину около 3.5×10-12. Такие вариации ходов бортовых часов GPS, с периодом около полусуток, были бы быстро и уверенно обнаружены – но о них не сообщается. А ведь если эти вариации имели бы место, то их интерпретация – через аддитивное действие земного и солнечного тяготений – не заставила бы себя ждать. Почему же об этих вариациях помалкивают? Ответ очевиден: потому что их нет. А, значит, нет и никакого «аддитивного» действия планетарного и солнечного тяготения.
Вместо этого, имеет место разграниченность областей действия солнечного и планетарных тяготений – малое пробное тело, где бы оно ни находилось, тяготеет либо только к планете, либо только к Солнцу (исключение – аномально организованное и короткодействующее тяготение Луны, которое наложено на земное тяготение (3.14)). В организации действия тяготения по такому, унитарному, принципу мы усматриваем большой смысл. Вспомним, что превращения энергии в «цифровом» мире должны происходить однозначно (1.3). При свободном падении тела изменяется его кинетическая энергия, однозначное значение которой зависит от квадрата локально-абсолютной скорости тела. А эта скорость определяется по отношению к локальному участку частотного склона. Значит, для однозначности превращений энергии при свободном падении, пробное тело должно иметь одну локально-абсолютную скорость, т.е. находиться только на одном частотном склоне – а, значит, солнечные и планетарные частотные склоны не должны накладываться друг на друга. Организация тяготения по унитарному принципу радикально упрощает не только мироустройство, но и расчёты движения малого тела – например, космического аппарата при межпланетном полёте. В рамках традиционного подхода, задача движения аппарата при его притяжени к нескольким силовым центрам – даже всего к двум! – уже не имеет аналитического решения. Унитарное же действие тяготения устраняет эту проблему. Где бы ни находился аппарат, он притягивается к одному силовому центру – и его движение описывается аналитически. Практика межпланетных полётов с очевидностью это подтверждает (2.6)! С учётом вышеизложенного, происхождение планет нам представляется следующим образом. В солнечный частотный склон встраивали частотную воронку будущей планеты и приводили её в орбитальное движение вокруг Солнца, а затем в эту воронку «загружали» вещество, из которого формировалась планета. При такой технологии, в результате загрузки в готовую воронку даже крупнодисперсных глыб вещества, глобальная фигура формируемой планеты мало отличалась бы от шаровой (см. также 6.10). В этой связи, мы не можем обойти молчанием такую аномалию в устройстве Солнечной системы, как отсутствие планетарной частотной воронки на орбите между Марсом и Юпитером. Согласно вышеупомянутому правилу Тициуса-Боде, там должна обращаться ещё одна планета, но вместо неё там имеет место пояс астероидов. Происхождение этого пояса астероидов официальная наука затрудняется объяснить. Действительно, чтобы развалить на обломки «гравитирующую» планету, следовало бы «совершить работу против сил гравитации». Это мог бы сделать достаточно мощный взрыв, но тогда разные обломки приобрели бы приращения к вектору орбитальной скорости, сильно различающиеся по величинам и направлениям. Поэтому траектории орбит обломков планеты, образовавшихся в результате её взрыва, имели бы огромный разброс параметров – и никакого пояса астероидов не было бы. Чтобы образовался пояс астероидов из планеты, её вещество должно было тихо рассредоточиться. Мы усматриваем здесь единственный разумный сценарий: по какой-то причине, частотная воронка планеты была отключена (ясно, что если программными манипуляциями возможно частотную воронку создать, то уничтожить её – тоже возможно). При этом, «отключилось» и планетарное тяготение, а вещество планеты могло рассредоточиться в результате срабатывания одних лишь сил упругости, до этого уравновешивавших силы гравитационного сжатия. Что касается воззрений официальной науки на пояс астероидов, то она ухватилась за гипотезу о том, что астероиды – это строительный материал, из которого планета так и не сформировалась. Указывают даже причину такой неудачи: влияние, каким-то образом, сильного гравитационного поля Юпитера. Эта версия не выдерживает критики, если иметь в виду, что в Солнечной системе планетарные частотные воронки, а, значит, и области планетарного тяготения, не перекрываются друг с другом. Орбита пятой планеты недосягаема для области действия тяготения Юпитера, поэтому формированию пятой планеты Юпитер никак не мог помешать. Ниже, в 3.9, мы проиллюстрируем это с особенной наглядностью.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.141.202 (0.013 с.) |
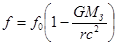 , (3.7.1)
, (3.7.1) . (3.7.2)
. (3.7.2)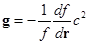 , (3.7.3)
, (3.7.3)


