
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оглушительные результаты гравиметрических измерений.
Поверхностные массы Земли распределены неоднородно. Там есть мощные горные массивы, с плотностью пород около трёх тонн на кубометр. Есть океаны, в которых плотность воды составляет всего тонну на кубометр – даже на глубине в 11 километров. Есть долины, лежащие ниже уровня моря – в которых плотность вещества равна плотности воздуха. По логике закона всемирного тяготения, эти неоднородности распределения масс должны действовать на гравиметрические инструменты. Простейшим гравиметрическим инструментом является отвес – успокоившись, он ориентирован вдоль местной вертикали. Издавна предпринимались попытки обнаружить уклонения отвеса, обусловленные притяжением, например, мощных горных массивов. Только роль отвеса здесь играл, конечно, не простой грузик на ниточке – ибо как можно знать, куда и насколько он отклонён? А использовался метод сравнения геодезических координат пункта измерений (получаемых, например, с помощью триангуляции) и его же координат, получаемых из астрономических наблюдений. Лишь во втором из этих методов используется привязка к местной вертикали, которая реализуется, например, с помощью ртутного горизонта у телескопа. Таким образом, по разнице координат пункта, полученных названными двумя методами, можно судить об уклонении местной вертикали. Так вот, результирующие уклонения в большинстве случаев оказались гораздо меньше тех, которые ожидались из-за действия горных массивов. Во многих учебниках по гравиметрии (см., например, [Ц1,Ш1]) упоминаются измерения, которые в середине 19-го века провели англичане южнее Гималаев. Там ожидались рекордные уклонения, ведь с севера находился самый мощный горный массив Земли, а с юга – Индийский океан. Но обнаруженные уклонения оказались почти нулевыми. Аналогичное поведение отвеса обнаруживается и вблизи морской береговой линии – вопреки ожиданиям того, что суша, более плотная, чем морская вода, будет притягивать отвес сильнее. Для объяснения подобных чудес учёные приняли гипотезу об изостазии. Согласно этой гипотезе, действие неоднородностей поверхностных масс скомпенсировано действием неоднородностей противоположного знака, находящихся на некоторой глубине. Т.е., под поверхностными плотными породами должны находиться рыхлые, и наоборот. Причём, эти верхние и нижние неоднородности должны, совместными усилиями, повсеместно обнулять действие на отвес – как будто никаких неоднородностей нет вовсе.
Знаете, когда читатели наших статей доходили до мест про изостазию, то они, не веря возможности такого лепета в современной науке, кидались, например, в Википедию – и убеждались, что всё так и есть. И – как они выражались – «от хохота падали пацтул». Ну, действительно: чем глубже океан, тем мощнее плотные компенсирующие залежи под его дном. А чем выше горы, тем на всё более рыхлом фундаменте они красуются. Причём, всё – тютелька в тютельку! Даже детям смешно! Но дети ещё не знают, что концепция изостазии прямо противоречит реалиям динамики земной коры [М1] – а то они смеялись бы ещё громче. Заметим, что уклонения отвеса свидетельствуют о горизонтальных компонентах местного вектора силы тяжести. Вертикальная же его компонента определяется с помощью гравиметров. С гравиметрами творятся те же самые чудеса, что и с отвесами. Но измерений с гравиметрами – очень много. Поэтому, чтобы народ не смешить, специалисты нагромоздили терминологические и методологические дебри, сквозь которые трудно продраться непосвящённому. Если публиковать прямые результаты гравиметрических измерений, то было бы слишком очевидно, что они не зависят от поверхностных неоднородностей масс. Поэтому прямые результаты пересчитывают, внося специальные поправки. Первая поправка, «за свободный воздух», или «за высоту», отражает нахождение пункта измерений на высоте, не совпадающей с уровнем моря (вблизи поверхности Земли эта поправка составляет около 0.3 мГал/м; 1 Гал = 1 см/с2). Вторая поправка отражает действие поверхностных неоднородностей масс. Сумму этих поправок называют поправкой Буге. Разность между измеренным и теоретическим значениями силы тяжести называют аномалией: без учёта второй поправки эта разность называется аномалией в свободном воздухе, а с учётом обеих – аномалией Буге. Теперь процитируем [Ш1]: «…пределы изменений аномалий в свободном воздухе должны быть от –350 мГал (для океана глубиной 5 км) до +450 мГал (для плоскогорья высотой 4 км). Аномалии Буге должны равняться нулю.
Однако оказалось, что результаты наблюдений противоречат этой теоретической зависимости. Аномалии в свободном воздухе почти не выходят за пределы ±50 мГал, а огромное большинство аномалий вообще близко к нулю. В то же время аномалии Буге в горных районах оказываются, как правило, отрицательными и довольно значительными по величине. Так, в западном Тибете, Памире, Куэнь-Луне аномалии Буге колеблются в пределах от –250 мГал до –550 мГал, в Мексиканском нагорье достигают –200 мГал, в Альпах –150 мГал. Напротив, в Атлантическом и Тихом океанах они имеют положительные значения от 300 до 400 мГал.» «…длинные полосы отрицательных аномалий… прослеживаются вдоль западного берега Южной и Центральной Америки, вдоль Алеутской островной дуги,… вдоль внешнего края дуги Суматра-Ява, вдоль Пуэрто-Рико, по дуге Южных Сандвичевых островов… Всюду эти аномалии или совпадают с глубоководными желобами, или идут по их краю». Таким образом, имеет место чёткая закономерность: если при гравиметрической съёмке не вводить поправок на влияние поверхностных масс, а использовать только поправку «за свободный воздух», то аномалии силы тяжести везде становятся близкими к нулю. Но считается, что поверхностные массы не могут не оказывать влияния на гравиметр, поэтому вычисляются и вносятся поправки, которые и дают аномалии, равные по величине этим поправкам. А затем, чтобы обнулить аномалии и привести теоретические значения в согласие с измеренными, применяют всё ту же остроумную гипотезу об изостазии. Думаете, не может быть такого плачевного состояния дел в науке? Может, может. А вот чего не может быть – так это изостатической компенсации. И по очень простой причине. Вот, пусть под поверхностью грунта находится локальное включение с повышенной плотностью, а под ним – компенсирующее включение с пониженной плотностью. Заметим, что если сила тяжести над этими включениями равна силе тяжести над участком с нормальной плотностью, то в стороне от этих включений компенсация уже не имеет места: изостатический диполь «притягивает» иначе, чем аналогичный участок с нормальной плотностью, что должно вызвать соответствующее уклонение отвеса. При заданном неоднородном распределении поверхностных масс, никаким распределением компенсирующих масс нельзя добиться сразу и нулевых уклонений отвеса, и нулевых аномалий силы тяжести: изостазия для отвесов и изостазия для гравиметров – несовместимы. На практике же повсеместно нулевые уклонения отвеса наблюдаются вместе с нулевыми аномалиями силы тяжести (если не вводить излишних поправок). Т.е. практика с полной очевидностью показывает: гравиметрические инструменты не реагируют на распределение масс. А почему? Наука до сих пор не выработала ответа на этот вопрос. А мы отвечаем: потому что массы не обладают притягивающим действием. И не только для поверхностных масс Земли справедлив этот вывод – гравиметрия позволяет обобщить его на всё вещество Земли. Это возможно с помощью измерений под поверхностью геоида, проводимых в шахтах или на борту погрузившегося под воду батискафа. Смотрите: согласно закону всемирного тяготения, земная сила тяжести в приближении, когда Земля считается однородным невращающимся шаром, максимальна на поверхности этого шара. Ведь, при подъёме над поверхностью, ускорение свободного падения уменьшается согласно выражению GM З/ r 2, где G - гравитационная постоянная, M З - масса Земли, r - расстояние до её центра. А, при погружении под поверхность, ускорение свободного падения уменьшается из-за того, что уменьшается «притягивающая» масса, поскольку равно нулю суммарное действие масс в поверхностном шаровом слое с толщиной, равной глубине погружения. При этом ускорение свободного падения линейно зависит от расстояния до центра Земли: GM З r/ R 3, где R - радиус Земли. Таким образом, в названном приближении, на поверхности Земли имел бы место излом (а также смена знака!) зависимости ускорения свободного падения от расстояния до центра Земли. Если же, как мы утверждаем, тяготение порождается не массами, и ускорение свободного падения не зависит от распределения масс, то и у зависимости ускорения свободного падения от высоты нет излома на поверхности Земли – функция ~1/ r 2 сохраняет свой вид при заглублении под поверхность. Именно это и показывают «сырые», нескорректированные данные измерений. Чтобы не афишировать эти убийственные для закона всемирного тяготения факты, авторы публикаций о тяготении в шахтах придерживаются следующих правил:
1) приводить данные лишь для уровней ниже поверхности, но не выше – чтобы не бросалось в глаза отсутствие «излома»; 2) не уточнять – увеличивается или уменьшается сила тяжести при погружении под поверхность; 3) не приводить «сырых» данных: приводить только данные, которые скорректированы хотя бы на действие поверхностных масс (а эти коррекции являются произволом: они зависят от принятой модели распределения поверхностных масс). При таких делах, почему же мы уверены в том, что в шахтах подтверждается не закон всемирного тяготения, а наша модель? Да повезло, знаете. Авторы статьи [С6], проводившие измерения в шахтах Квинсленда (Австралия), опубликовали-таки «сырые» данные (Табл.1, колонка 3). Причём, чётко указали, что представлены значения, измеренные на глубине, минус значение, измеренное на поверхности – откуда сразу ясно, что ускорение свободного падения увеличивается при погружении, а не уменьшается, как требует закон всемирного тяготения. Более того! Обратите внимание: согласно этому закону, модуль производной у высотной зависимости ускорения свободного падения при подходе к точке излома сверху, 2 GM З / R 3, в два раза больше чем при подходе к точке излома снизу, GM З / R 3. При задействованном перепаде глубин D h =948.16 м [С6], расчётная величина приращения ускорения свободного падения 2 GM ЗD h/ R 3, т.е. при надповерхностном значении производной, составляет»2.96×10-3 м/с2. Сравните с ней измеренное значение для названного перепада глубин: 2.9274×10-3 м/с2 [С6]. Совершенно очевидно: при переходе через поверхность Земли сверху вниз, не имеет место не только смена знака, но и двукратное уменьшение модуля производной у высотной зависимости ускорения свободного падения. Такое возможно, если всё вещество Земли не обладает притягивающим действием! Мы обнаруживаем здесь, прямо скажем, глобальный прокол закона всемирного тяготения – наша же модель подтверждается и качественно, и количественно.
Знаете, один писатель, приближённый к военным кругам, красочно описывал, как наши атомные подводные лодки легко отрывались от американских, закладывая лихие виражи между подводных гор Срединно-Атлантического хребта. Это, якобы, потому, что на наших лодках были гравитационные детекторы подводных гор, а у американцев такой прелести не было. Ну, ну. Знал бы этот писатель о положении дел в гравиразведке полезных ископаемых. Практикам-то известно, что, несмотря на хорошо разработанную теорию, эффективность гравиразведки является наихудшей по сравнению с эффективностями других методик – например, сейсмической или электромагнитной. Показания гравиметров и вариометров (приборов на основе крутильных весов) лишь в ничтожном проценте случаев отражают истинную картину залегания тех или иных пород. И эти редкие случаи происходят просто потому, что если прибор указывает направление совершенно случайно, то рано или поздно он укажет его правильно. Неужто нашёлся бы капитан подводной лодки, который доверял бы подобным приборам? Или, пардон, на подводных лодках гравитационные детекторы – какие-то особенные? Основанные на том, что «в боевой обстановке значение синуса может приближаться к четырём»! Эх, а ведь до сих пор разные организации предлагают простакам услуги по гравиметрической разведке. Разведка пешая! Автомобильная! С борта самолёта! Со спутников! «Любые фантазии клиентов – за их денежки!» Причём, ведь гравиметрические карты рисуют – разноцветные! Ну, что тут скажешь. Во-первых, красиво. А, во-вторых, кому эти картинки мешают?
3.4 Малые планеты: как же они ускоряются к Солнцу? Из закона всемирного тяготения следует, что притяжение к нескольким массивным телам равно векторной сумме притяжений к каждому из них по отдельности. Т.е., тяготения нескольких тел действуют совместно, аддитивно. Такой подход приводит к поразительному парадоксу; мы изложим его в терминах гравитационных потенциалов. Тело, имеющее собственное тяготение, находится в центре собственной потенциальной ямы. Быть в этой яме означает быть в устойчивом равновесии. Отчего же малое тело, находясь вблизи много большего тела, ускоряется к нему? Оттого, говорят нам, что потенциальная ямка малого тела, складываясь с потенциальным склоном большого тела, возмущает этот склон настолько слабо, что суммарное распределение потенциала в объёме малого тела представляет собой, в первом приближении, склон, а не ямку – а по склону тело должно «скатываться». Очень хорошо! Теперь пусть малое тело удаляется всё дальше от большого. При этом крутизна потенциального склона большого тела становится всё меньше, и, наконец, она сравняется с крутизной потенциальной ямки малого тела на его поверхности. Расстояние от большого тела, на котором это произойдёт, мы называем дальностью отчуждения. За пределами дальности отчуждения малое тело находится уже не «на склоне», а «в ямке». Конечно, эта «ямка» асимметрична из-за перекоса, наводимого склоном большого тела – но теперь это, в первом приближении, ямка, а не склон. А в ямке тело должно удерживаться. С чего ему теперь «скатываться» в сторону большого тела? В перекошенной ямке у тела будет другое положение равновесия и другое распределение деформаций, чем в симметричной ямке, но перекошенная ямка будет удерживать тело не хуже, чем симметричная. Таким образом, из аддитивности действия тяготения следует вывод: малое тело, находящееся за пределами дальности отчуждения от большого тела, не должно к нему ускоряться. Но практика не подтверждает этот вывод.
Действительно, для малого тела с массой m и радиусом r, дальность отчуждения Dот от большого тела с массой M, в предположении справедливости закона всемирного тяготения, есть
В таблице приведены рассчитанные по этой формуле дальности отчуждения от Солнца для некоторых малых планет (a – расстояние от Солнца в афелии; справочные данные взяты из [К2]).
Как можно видеть, расстояния от Солнца, на которых малые планеты, несомненно, ускоряются к нему, на порядок превосходят соответствующие дальности отчуждения. Как такое возможно? Парадокс легко разрешался бы, если у малых планет, действительно, не было бы собственного тяготения, т.е. не было бы собственных потенциальных ямочек. Тогда для них не было бы и дальностей отчуждения от Солнца, и они могли бы ускоряться к нему в пределах всей области действия солнечного тяготения – что и происходит в действительности.
3.5 Где же притягивающее действие у спутников планет? В Солнечной системе собственное тяготение с полной очевидностью имеется у Солнца, планет и Луны. Что касается остальных спутников планет, то мы обнаруживаем следующее. Во-первых, даже в случаях самых крупных спутников (в том числе и Титана) не обнаружена динамическая реакция их планет – ведь, в согласии с законом всемирного тяготения, планета должна обращаться вокруг общего со спутником центра масс. Во-вторых, о тяготении спутников планет свидетельствовало бы наличие у них атмосфер. Но, за исключением Титана, явных признаков атмосфер ни у кого из них не обнаружено. В-третьих, ни у кого из шести десятков известных на сегодня спутников планет не обнаружено ни одного собственного спутничка. В свете теории вероятностей, такое положение вещей выглядит довольно-таки странным. В-четвёртых, особого упоминания заслуживают т.н. динамические определения масс спутников, основанные на аксиоме о том, что спутники одной планеты непременно возмущают движение друг друга. Если в действительности спутники не притягивают друг друга, то динамические определения их масс являются попытками решения некорректно поставленной задачи. И признаки этого – действительно налицо: результаты применения этой методики оказываются расплывчатыми и неоднозначными. Вот комментарии определения де Ситтером масс четвёрки крупных спутников Юпитера, на основе полученного им периодического решения: «Фактические орбиты спутников не соответствуют в точности периодическому решению, но могут быть получены из периодического решения вариацией координат и компонент скорости…», и далее: «…трудностью является медленная сходимость аналитического разложения по степеням масс» [М2]. Тем не менее, значения масс, «данные де Ситтером, следует считать наилучшими… Всякое уточнение этих значений потребовало бы построения новой теории, …потребовался бы также новый ряд наблюдений положений этих спутников» [Д1]. Выбранные здесь «наиболее вероятные» значения масс спутников – из набора не повторяющихся значений – едва ли могут служить доказательством того, что спутники действительно притягивают друг друга. Скорее, мы имеем свидетельство о том, что притягивающего действия у них как раз нет. Конечно, вышеперечисленные свидетельства являются косвенными и «ничего не доказывающими». Мало ли бывает странных совпадений! Но на сегодня-то известны и прямые свидетельства об отсутствии притягивающего действия спутников планет – да такие прямые, что прямее не бывает. Эти свидетельства добыты с помощью космического зонда КАССИНИ, который около десяти лет, начиная с 2004 года, работал в окрестностях Сатурна. Одной из его главных задач был сбор информации о спутниках Сатурна, поэтому свободный полёт зонда время от времени подправлялся так, чтобы зонд прошёл недалеко от того или иного спутника. Зонд был оснащён оборудованием, предназначенным для определения массы «гравитирующего тела» при близком пролёте. Смотрите: по ходу пролёта рядом с этим телом, зонд сначала приближается к нему, а потом удаляется от него. При свободном движении в центральном поле тяготения справедливо выражение [Л4]:
где v – скорость движения, GM - гравитационный параметр притягивающего центра, т.е. произведение гравитационной постоянной на его массу, r - расстояние до притягивающего центра. В случае движения «из бесконечности», когда (1/ r 0)=0, гравитационный параметр выражается следующим образом: GM» V ×D V × R, (3.5.2) где V – подлётная скорость, D V – приращение скорости по достижении точки наибольшего сближения, R – расстояние до притягивающего центра от точки наибольшего сближения. Изменение скорости зонда вызывает соответствующее изменение допплеровского сдвига при радиосвязи с Землёй. По величине пролётного допплеровского «провала» находят приращение скорости D V и, зная подлётную скорость V и расстояние наибольшего сближения R, находят гравитационный параметр космического тела. Эта методика хорошо зарекомендовала себя, например, при пролёте рядом с Меркурием зонда «Маринер-10» [Г18] (см. также [Г19]). Утверждалось [Р2,П6], что именно эта методика использовалась для определения масс спутников Сатурна. Некоторые из них – например, Рея, Япет, Диона, не говоря уже про Титан – по размерам сопоставимы с Меркурием, и КАССИНИ совершил множество пролётов рядом с ними, включая пролёты «впритирку», на нескольких десятках километров от поверхности. Однако в официальных научных материалах [П6,А8], посвящённых движению КАССИНИ в окрестностях Сатурна, на диаграммах с допплеровскими данными нам не демонстрируют ни одного пролётного «провала». Ничуть не конфузясь, специалисты из NASA поясняют, что значения масс спутников получались совсем по-другому, методом оптимизации многих параметров, в число которых входили эти массы: «На каждом обрабатываемом сегменте траектории оценивались, помимо гравитационного параметра Сатурна, ещё и гравитационные параметры его девяти главных спутников» [П6]. Зачем же специалистам из NASA пришлось прибегать к методу оптимизации многих параметров, который применяется для высоконаучных доказательств наличия того, что в реальности не существует? Ответ для нас очевиден [Г20]: затем, что честные допплеровские данные говорили о том, что спутники Сатурна не вносят гравитационных возмущений в полёт КАССИНИ, т.е. что собственным тяготением спутники Сатурна не обладают! Жаль, что об этом не подозревают учёные, которых впечатлили гейзеры на Энцеладе, сфотографированные тем же КАССИНИ. Учёные теряются в догадках – какие же это мощные энергетические процессы должны происходить внутри космической ледышки («icy moon»), чтобы струи паров и кристалликов льда взлетали на сотни километров над поверхностью и свободно уходили в космос. Если бы учёные знали, что у Энцелада нет собственного тяготения – а с помощью КАССИНИ это доказано! – то разгадка взлёта и ухода в космос струй паров и кристалликов льда была бы совсем простой. Да что там Энцелад! С помощью КАССИНИ доказано, что собственного тяготения нет и у Титана. При близких пролётах от Титана, притормаживание КАССИНИ об его атмосферу регистрировалось [А8], а гравитационные возмущения полёта – нет! Нас пытаются убедить в том, что отсутствие этих гравитационных возмущений меркнет перед фактом наличия у Титана атмосферы. Один этот факт, якобы, доказывает наличие собственного тяготения у Титана – ибо чем же удерживается его атмосфера, если не его тяготением? Увы, в том и дело, что атмосфера Титана совсем им не удерживается. Она стекает с него настолько интенсивно, что вдоль всей орбиты Титана (с радиусом около 20 радиусов Сатурна) существует огромное газовое облако, порождаемое этим стоком – т.н. тор Титана [М5]. Про тор Титана было хорошо известно уже в 80-х годах ХХ века (см., например, [С7]) – благодаря анализаторам ультрафиолета на бортах американских аппаратов «Пионер-11» и «Вояджер-1,2». Здесь вопиющим фактом является то, что сток атмосферы Титана происходит не изотропно, а, практически, в одну сторону – противоположно вектору орбитальной скорости Титана, отчего за Титаном тянется газовый хвост. При допущении собственного тяготения у Титана, такой анизотропный сток атмосферы является чудом, для возможности которого нужно, чтобы поле тяготения Титана было не центрально-симметричным, как того требует закон всемирного тяготения, а имело бы, извините за выражение, «задний проход», т.е. створ, в котором тяготение отключено или, по крайней мере, сильно ослаблено. Допущение такого створа является абсурдом с позиций закона всемирного тяготения, поэтому попытки объяснения газового хвоста Титана зашли в тупик. Между тем, феномен газового хвоста Титана объясняется просто и естественно при допущении отсутствия у Титана собственного тяготения [Г20] – в согласии с допплеровскими данными (см. выше). Газовый хвост свидетельствует о том, что происходит, фактически, свободный сток атмосферы Титана. И если при этом атмосфера Титана не иссякает, то логично допустить, что она постоянно пополняется, т.е. что поверхность Титана «газит». Даже если газовыделение происходит на всех участках поверхности с примерно одинаковой интенсивностью, свободный сток атмосферы должен быть несимметричен из-за того, что Титан движется с орбитальной скоростью 5.55 км/с и оказывает соответствующее динамическое давление на переднюю часть атмосферы. Но Титан – такой большой спутник, что, в вопросе о его «собственном тяготении», двух проколов (с данными «пролётной методики» и со свободным стоком его атмосферы) оказалось недостаточно. Устроили ещё один прокол – с парашютной посадкой на Титан зонда ГЮЙГЕНС, выпущенного с того же КАССИНИ. Даже дети знают, что парашютный спуск используется для того, чтобы замедлить скорость падения, обусловленного тяготением. На эту детскую логику и рассчитывали организаторы парашютного шоу с зондом ГЮЙГЕНС. Цель была достигнута: «Как может у Титана не быть собственного тяготения, - вопрошают нас, - если ГЮЙГЕНС спускался в атмосфере Титана на парашютах?!» Отвечаем [Г20]: в данном случае парашюты, при движении сквозь атмосферу, можно было с успехом использовать и при отсутствии тяготения – просто для гашения остатка скорости, которая на подлёте к атмосфере составляла около 6 км/с. ГЮЙГЕНС следовало направить так, чтобы он попал в Титан по инерции. После торможения в верхних слоях атмосферы до скорости, меньшей скорости звука, уже можно было использовать парашюты – с таким расчётом, чтобы скорость зонда при контакте с поверхностью составила несколько метров в секунду. Эта задача, которая была решена блестяще, не представляет, на наш взгляд, особых сложностей – при наличии на ГЮЙГЕНСе акселерометра, высотомера и надлежащим образом запрограммированного процессора, для автономного управления раскрытием и отделением парашютов. И вот что изумляет: самый большой парашют, с диаметром 8.3 метра, использовался не на последнем этапе спуска, а на предпоследнем – на последнем же этапе использовался парашют с гораздо меньшим диаметром: 3 метра [ВЕБ31,ВЕБ32]. Что мешало закончить спуск на большом парашюте? Зачем понадобилось идти на дополнительный риск и раскрывать другой парашют? И почему этот парашют малый? – неужели хотелось побыстрее достигнуть поверхности, да воткнуться в неё на повышенной скорости? Нет, тут детская парашютная логика не работает. Парашютные спуски при наличии тяготения и при его отсутствии – существенно различаются. В первом случае, на аппарат действуют две главные силы – сила тяжести и сила парашютного торможения – величины которых, в установившемся режиме, равны, поэтому аппарат снижается с постоянной скоростью. Во втором же случае, на аппарат действует одна главная сила – сила парашютного торможения – поэтому аппарат снижается, непрерывно теряя скорость. Напрашивается вывод: самый большой парашют ГЮЙГЕНСа тормозил слишком сильно, так что аппарат потерял бы всю скорость, не достигнув поверхности Титана. Поэтому и сделали замену на меньший парашют, чтобы обеспечить достижение поверхности. Кстати, вращавшаяся видеокамера ГЮЙГЕНСа снимала панораму в течение всего парашютного спуска [ВЕБ31,ВЕБ32], но до оригинала этого фильма нам не удалось добраться. Вместо оригинала, в Интернете выложена поделка, состряпанная средствами компьютерной анимации. А что же за страшные секреты содержатся в оригинале? Например, если вход в атмосферу не был строго вертикален, то, при наличии тяготения, снижение на завершающем участке выходило бы на отвесную линию – а, при отсутствии тяготения, снижение продолжалось бы в направлении, заданном при входе в атмосферу, и, по мере приближения к поверхности, снижение всё больше отличалось бы от отвесного. Может, по мере приближения к поверхности, видеокамера, действительно, фиксировала всё больший крен горизонта? Такое, конечно, нельзя показывать… Так или иначе, но правду от нас скрывают. А если правду от нас скрывают, то как можно верить тому, что нам говорят?
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 61; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.240.243 (0.05 с.) |
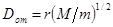 . (3.4.1)
. (3.4.1)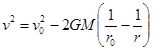 , (3.5.1)
, (3.5.1)


