
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение состояния идеальных газовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Законы Бойля-Мариотта, Гей-Люссака и Шарля устанавливают связь только между двумя из трех основных параметров идеального газа – Уравнение состояния устанавливает связь между тремя основными параметрами идеального газа. Переведем идеальный газ, заключенный в цилиндре под поршнем с параметрами Сначала уменьшим давление газа от Рассмотрим изменение параметров газа при этих переходах. Так как на первом этапе переход газа из одного состояния в другое происходит при постоянной температуре, то по закону Бойля-Мариотта:
откуда
На втором этапе переход происходит при постоянном давлении, поэтому согласно закону Гей-Люссака
откуда
В уравнениях (3.4) и (3.5) правые части равны одной и той же величине, т.е. можно записать:
Начальные и конечные состояния газа были выбраны произвольно, поэтому отношение произведений давления на удельный объем к температуре в любом состоянии идеального газа равны между собой:
Эту постоянную величину называют удельной газовой постоянной. Обозначив ее буквой
или
Уравнение (3,6) называется уравнением состояния идеального газа или уравнением Клапейрона. Если умножить левую и правую части этого уравнения на произвольную массу газа
или
Закон Авагадро Закон Авогадро (1802 г,) первоначально формулировался так: все идеальные газы содержат в равных объемах при одинаковых давлении и температуре одинаковое число молекул. Поскольку в одном и том же количестве вещества содержится одно и тоже число его частиц, современная формулировка закона Авогадро следующая: в равных объемах любых идеальных газов при одинаковых давлениях и температуре содержится одно и тоже количество вещества. Из этого определения и уравнения (1.1) следует, что молярный объем любого идеального газа при одинаковых давлении и температуре один и тот же. Этот вывод можно распространить и на реальные газы при относительно невысоких давлениях и относительно высокой температуре. На основании научных исследований значение молярного объема идеальных газов при нормальных физических условиях (
По известному значению молярной массы идеального газа (
Уравнение Менделеева Умножим обе части уравнения состояния идеального газа (3.6) на молярную массу (
после подстановки
или
Правая часть последнего уравнения – величина, имеющая одно и то же значение для всех идеальных газов, так как в соответствии с законом Авогадро объем любого идеального газа при одинаковых давлениях и температуре один и тот же. Из этого следует, что и левая часть уравнения является одинаковой для всех идеальных газов, поэтому она называется универсальной или молярной газовой постоянной и обозначается
Поэтому можно записать
Уравнение (3.12) было выведено Д.И. Менделеевым для количества вещества
Следовательно, уравнение Менделеева можно записать:
Из уравнения (3.11) можно получить удельную газовую постоянную(
Это уравнение очень удобно для вычисления газовой постоянной, так как для ее определения нужно знать только значение молярной массы, числовое значение которой, как уже говорилось, равно относительной молекулярной массе. Для примера найдем газовую постоянную углекислого газа СО 2. Так как относительная молекулярная масса этого газа
Пользуясь уравнением (3.13), можно определить молярный объем идеального газа при любых давлениях и температуре:
Умножая обе части уравнения (3.11) на количество вещества
или
что является другой формой записи уравнения Менделеева. Примеры решения задач Пример 3.1 Резервуар вместимостью 4 м3 заполнен углекислым газом. Найти массу газа и его вес, если избыточное давление в резервуаре 40 кПа, температура 80 оС, а барометрическое давление 102,4 кПа. Решение Абсолютное давление газа равно:
Из уравнения состояния найдем массу газа:
Вес газа равен:
Пример 3.2 В баллоне содержится кислород массой 2 кг при давлении 8,3 МПа и температуре 15 оС. Вычислить вместимость баллона. Решение Из уравнения состояния (3.7) получим:
Значение R взято из приложения 1. 3.7. Задачи для самостоятельного решения 3.1. Для автогенной сварки привезен баллон кислорода вместимостью 100 л. Найти массу кислорода, если его давление 10,8 МПа при температуре 17 оС. Наружное давление 100 кПа. Ответ: 14,45 кг. 3.2. В баллоне массой 117 кг и вместимостью 100 л содержится кислород при температуре 20 оС. Определить давление кислорода в баллоне, если масса порожнего баллона 102 кг. Ответ: 11,42 МПа. 3.3. Давление кислорода в баллоне вместимостью 100 л равно 883 кПа при температуре 20 оС. Определить массу кислорода, который нужно подкачать в баллон, чтобы повысить давление в нем до 10,2 МПа при температуре 70 оС. Наружное давление 101 кПа. Ответ: 10,27 кг. 3.4. По трубопроводу протекает кислород при температуре 127 оС и давлении по манометру 294 кПа. Найти массовый расход кислорода, если объемный расход его составляет 10 м3/мин Ответ: 28,3 кг/мин. 3.5. Найти объем 1 кмоль газа при давлении 0,5 МПа и температуре 30 оС. Ответ: 5,04 м3.
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.231 (0.007 с.) |

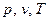 при условии, что значение третьего остается неизменным.
при условии, что значение третьего остается неизменным.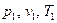 , в состояние с параметрами
, в состояние с параметрами 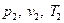 . Осуществим этот переход в два этапа.
. Осуществим этот переход в два этапа.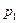 до
до 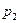 , поддерживая температуру
, поддерживая температуру 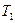 постоянной путем подвода к газу определенного количества теплоты. Вследствие этого газ окажется в некотором промежуточном состоянии с параметрами
постоянной путем подвода к газу определенного количества теплоты. Вследствие этого газ окажется в некотором промежуточном состоянии с параметрами 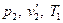 . Затем при неизменном давлении будем подогревать газ до конечной температуры
. Затем при неизменном давлении будем подогревать газ до конечной температуры 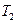 и удельного объема
и удельного объема 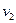 .
.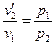 ,
,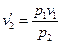 . (3.4)
. (3.4)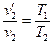
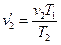 . (3.5)
. (3.5)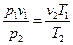 или
или 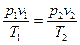
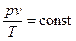
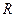 , получим:
, получим: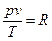
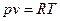 . (3.6)
. (3.6)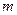 , то получим:
, то получим: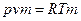
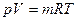 , (3.7)
, (3.7)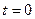 оС и
оС и 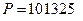 Па) принято равным:
Па) принято равным: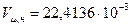 м3/моль (приближенно 22,4 м3/кмоль).
м3/моль (приближенно 22,4 м3/кмоль).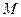 ) можно определить его удельный объем (
) можно определить его удельный объем (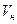 ) и плотность (
) и плотность (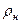 ) при нормальных физических условиях:
) при нормальных физических условиях: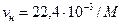 ; (3.8)
; (3.8)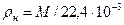 , (3.9)
, (3.9)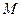 ), получим:
), получим: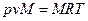 , (3.10)
, (3.10)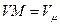 получим:
получим: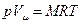
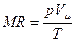 .
.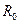 :
: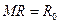 . (3.11)
. (3.11)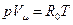 . (3.12)
. (3.12)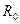 . Для этого подставим в уравнение (3.12) значения:
. Для этого подставим в уравнение (3.12) значения: 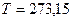 К,
К, 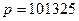 Па и
Па и 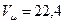 м3/кмоль, получим:
м3/кмоль, получим: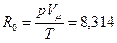 Дж/(моль∙К).
Дж/(моль∙К).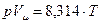 . (3.13)
. (3.13)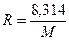 . (3.14)
. (3.14)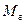 = 44,01, то молярная масса его
= 44,01, то молярная масса его 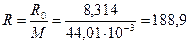 Дж/кг∙К.
Дж/кг∙К.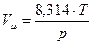 .
.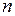 , получим
, получим
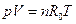 ,
,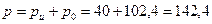 кПа.
кПа.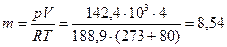 кг.
кг.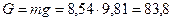 Н.
Н.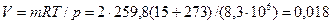 м3.
м3.


