
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение истинных и средних теплоёмкостейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для нахождения истинных теплоемкостей чаще всего используется табличный способ. Средняя удельная теплоёмкость в интервале температур
В приложении 2 приведены истинные удельные теплоёмкости воздуха и отдельных газов. Теплоёмкость смесей На практике чаще всего приходится сталкиваться не с отдельными газами, а с их смесями, поэтому необходимо знать определение теплоемкости смеси. При нагревании газовой смеси подведенная теплота расходуется на нагревание отдельных ее компонентов, и теплоемкость смеси определяется по ее составу. При задании смеси массовыми долями подведенную теплоту можно определить следующим образом:
или
где следовательно,
Деля левую и правую части последнего уравнения на
Но поскольку
Таким образом, массовая теплоемкость смеси равна сумме произведений массовых теплоемкостей газов, входящих в смесь, на их массовые доли. При задании смеси объемными долями, учитывая, что
т.е. объемная теплоемкость газовой смеси равна сумме произведений объемных теплоемкостей газов, входящих в состав смеси, на их объемные доли. При задании смеси молярными долями, исходя из того, что объемные и мольные доли равны, запишем:
т.е. молярная теплоемкость газовой смеси равна сумме произведений молярных теплоемкостей газов, входящих в состав смеси, на их молярные доли. Примеры решения задач Пример 5.1 При постоянном давлении найти среднюю удельную массовую теплоёмкость кислорода при повышении его температуры от 600 до 2000 оС. Решение Искомую теплоёмкость принимаем равной истинной удельной изобарной теплоёмкости при средней арифметической температуре (
Находим в приложении 2 истинную удельную изобарную теплоёмкость кислорода при температуре 1300 оС: Пример 5.2 Найти среднюю молярную изобарную теплоёмкость углекислого газа Решение. Найти эту теплоёмкость можно найти из первого соотношения (5.1), из которого получаем:
Предварительно находим молярную массу (М). Относительная молярная масса углекислого газа Мг = 44,01. Следовательно, его молярная масса РАВНА: М = 44,01·10-3 кг/моль. Среднюю удельную изобарную теплоёмкость (
Из приложения 2 находим, что при этой температуре искомая истинная удельная теплоёмкость
Теперь можно найти искомую среднюю молярную изобарную теплоёмкость:
Пример 5.3 Воздух, содержащийся в баллоне вместимостью 12,5 м3 при температуре 20 оС и абсолютном давлении 1МПа, подогревается до температуры 180 оС. Найти подведённую теплоту Q. Решение Из определения удельной теплоемкости с учетом того, что процесс нагревания происходит при постоянном объеме, можно записать:
откуда
Принимая во внимание, что при температуре
где Среднюю удельную изохорную теплоёмкость принимаем равной истинной теплоёмкости при средней температуре воздуха 100 оС, т.е.
Следовательно, искомое количество подведенной теплоты равно:
Пример 5.4 Температура смеси, состоящей из азота массой 3 кг и кислорода массой 2 кг, в результате подвода к ней теплоты при постоянном объёме повышается от 100 до 1100 оС. Найти количество подведённой теплоты. Решение Искомое количество теплоты (Q) найдем из выражения:
Среднюю удельную изохорную теплоёмкость смеси найдём согласно уравнению:
где По условию задачи масса смеси азота кислорода Для нахождения теплоёмкостей компонентов смеси
При этой температуре: для азота для кислорода Найдем теплоёмкость смеси:
Подведённая к смеси теплота равна:
Пример 5.5 Состав продуктов сгорания бензина в цилиндре двигателя внутреннего сгорания в молях следующий: углекислого газа СО2 – 71,25, кислорода О2 – 21,5, азота N 2 – 488,3; паров воды Н2О – 72,5. Температура газов 800 оС. Определить долю тепловых потерь с уходящими газами, если теплота сгорания бензина 43950 кДж/кг. Решение Найдём сначала теплоту (Q 1) уходящих газов. Предположим, что сгорание происходит при постоянном давлении, поэтому можно записать:
где При среднеарифметической температуре процесса
средние удельные теплоёмкости компонентов, а также их молярные массы согласно даным, представленных в приложении 2, равны: для углекислого газа для кислорода для азота паров воды По найденным значениям удельных теплоёмкостей и молярных масс вычислим значения молярных теплоёмкостей компонентов смеси: углекислого газа
кислорода
азота
паров воды
Найдем количество теплоты, уносимой смесью (выхлопными газами):
Обозначив теплоту сгорания бензина через Q, получим, что потеря теплоты с выхлопными газами в процентах составляет:
5.6. Задачи для самостоятельного решения 5.1. Найти средние удельные изохорную и изобарную теплоёмкости кислорода в интервале температур 1800…1200 оС. Ответ: 5.2. Найти среднюю молярную изохорную теплоёмкость кислорода при нагревании его от 0 до 1000 оС. Ответ: 25,3 кДж/(моль·К), 5.3. В помещении размером 6х5х3 м температура воздуха 27 оС при давлении 101 кПа. Найти количество теплоты, которую нужно отвести от этого воздуха, чтобы понизить его температуру до 17 оС при том же давлении. Средняя удельная изобарная теплоёмкость воздуха 1,004 кДж/(кг·К). Массу воздуха в помещении условно принять постоянной. Ответ: 1,06 МДж. 5.4. От азота, заключённого в баллоне, отводится 1700 кДж теплоты. При этом температура его понижается от 800 до 200 оС. Найти массу азота, заключённого в баллоне. Ответ: 34,6 кг. 5.5. В трубчатом воздухоподогревателе воздух нагревается при постоянном давлении от 10 до 90 оС. Найти массовый расход воздуха, проходящего через воздухоподогреватель, если ему сообщается 210 МДж/ч теплоты. Ответ: 2610 кг/ч. 5.6. Найти средние изобарную и изохорную молярные теплоёмкости продуктов сгорания топлива при охлаждении их от 1100 до 300 оС. Молярные доли компонентов этих продуктов сгорания следующие: Ответ: 5.7. Состав отработавших газов двигателя внутреннего сгорания в молях следующий: Ответ: 13,84 МДж Первое начало термодинамики
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 2422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.253 (0.007 с.) |

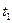 и
и 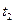 может быть принята как среднеарифметическая между истинными теплоёмкостями
может быть принята как среднеарифметическая между истинными теплоёмкостями 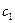 (при температуре
(при температуре 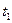 ) и
) и 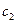 (при температуре
(при температуре 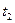 ), т.е.
), т.е.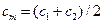 .
.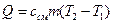
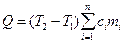 ,
,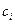 ,
, 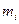 - удельная теплоемкость и масса i -го компонента соответственно,
- удельная теплоемкость и масса i -го компонента соответственно, .
.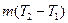 , получим:
, получим: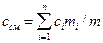 .
.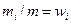 – массовая доля i –того компонента, то можно записать
– массовая доля i –того компонента, то можно записать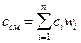 .
.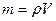 и
и 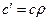 , получим:
, получим: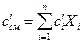 ,
,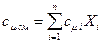 ,
,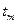 ):
):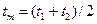 = (600 + 2000) / 2 = 1300 оС
= (600 + 2000) / 2 = 1300 оС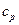 = 1,1476 кДж/(кг·К). Это значение теплоёмкости равно средней удельной изобарной теплоёмкости
= 1,1476 кДж/(кг·К). Это значение теплоёмкости равно средней удельной изобарной теплоёмкости 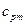 кислорода в интервале температур 600…2000 оС.
кислорода в интервале температур 600…2000 оС.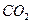 при повышении его температуры от 200 до 1000 оС.
при повышении его температуры от 200 до 1000 оС.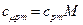 .
.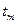 . В нашем примере эта температура равна:
. В нашем примере эта температура равна: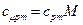 = 1,1962 · 44,01·10-3 = 52,89 кДж/(моль·К).
= 1,1962 · 44,01·10-3 = 52,89 кДж/(моль·К). ,
,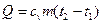 .
.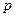 = 1 МПа, массу воздуха (
= 1 МПа, массу воздуха (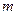 ) найдём из уравнения состояния:
) найдём из уравнения состояния: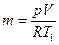 = 1·106 · 12,5 / (287,1 · 293) = 148,6 кг,
= 1·106 · 12,5 / (287,1 · 293) = 148,6 кг,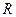 = 287,1 Дж/(кг·К) – удельная газовая постоянная воздуха (см. приложение 1).
= 287,1 Дж/(кг·К) – удельная газовая постоянная воздуха (см. приложение 1).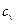 = 722,6Дж/(кг·К).
= 722,6Дж/(кг·К).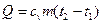 = 722,6 · 148,6·(180 – 20) = 17,2 МДж.
= 722,6 · 148,6·(180 – 20) = 17,2 МДж. .
.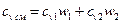 ,
,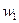 и
и 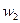 – массовые доли компонентов азота и кислорода.
– массовые доли компонентов азота и кислорода. = 3 + 2 = 5 кг. Следовательно, массовая доля равна:
= 3 + 2 = 5 кг. Следовательно, массовая доля равна: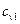 и
и 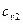 воспользуемся приложением 2. Примем, что они равны истинной удельной изохорной теплоёмкости при средней арифметической температуре:
воспользуемся приложением 2. Примем, что они равны истинной удельной изохорной теплоёмкости при средней арифметической температуре: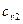 = 809 Дж/(кг·К).
= 809 Дж/(кг·К).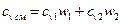 = 0,6 · 843 + 0,4 · 0,809 = 829 Дж/(кг·К)
= 0,6 · 843 + 0,4 · 0,809 = 829 Дж/(кг·К)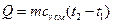 = 5·829·(1100 – 100) = 4,1 МДж.
= 5·829·(1100 – 100) = 4,1 МДж.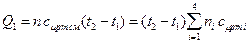 ,
,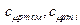 – средние молярные изобарные теплоёмкости соответственно всей смеси и её компонентов;
– средние молярные изобарные теплоёмкости соответственно всей смеси и её компонентов; 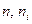 – количество вещества соответственно всей смеси и её компонентов.
– количество вещества соответственно всей смеси и её компонентов.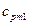 = 1,11 кДж/(кг·К), М1 = 44·10-3 кг/моль;
= 1,11 кДж/(кг·К), М1 = 44·10-3 кг/моль;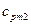 = 1,02 кДж/(кг·К), М2 = 32·10-3 кг/моль;
= 1,02 кДж/(кг·К), М2 = 32·10-3 кг/моль;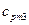 = 1,09 кДж/(кг·К), М3 = 28·10-3 кг/моль;
= 1,09 кДж/(кг·К), М3 = 28·10-3 кг/моль;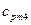 = 2,08 кДж/(кг·К), М4 = 18·10-3 кг/моль.
= 2,08 кДж/(кг·К), М4 = 18·10-3 кг/моль.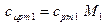 = 1,11·44·10-3 = 48,84 Дж/(моль·К);
= 1,11·44·10-3 = 48,84 Дж/(моль·К);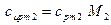 = 1,02·32·10-3 = 32,64 Дж/(моль·К);
= 1,02·32·10-3 = 32,64 Дж/(моль·К);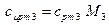 = 1,09·28·10-3 = 30,52 Дж/(моль·К);
= 1,09·28·10-3 = 30,52 Дж/(моль·К);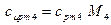 = 2,06·18·10-3 = 37,08 Дж/(моль·К).
= 2,06·18·10-3 = 37,08 Дж/(моль·К).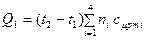 ;
;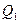 = 800·(71,25 · 48,84 + 21,5 · 32,64 + 488,3 · 30,52 + 72,5 · 37,08) = 17,418 кДж.
= 800·(71,25 · 48,84 + 21,5 · 32,64 + 488,3 · 30,52 + 72,5 · 37,08) = 17,418 кДж.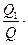 100 = (17418 / 43950)·100 = 39,6 %.
100 = (17418 / 43950)·100 = 39,6 %.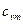 = 0,9 кДж/(кг·К);
= 0,9 кДж/(кг·К); 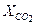 = 0,09;
= 0,09; 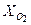 = 0,083;
= 0,083; 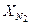 = 0,758,
= 0,758, 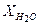 = 0,069.
= 0,069.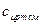 = 32,3 Дж/(моль·К);
= 32,3 Дж/(моль·К); 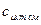 = 27,0 Дж/(моль·К).
= 27,0 Дж/(моль·К).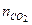 = 74,8;
= 74,8; 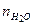 = 68;
= 68; 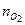 = 119;
= 119; 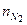 = 853. Найти количество теплоты, выделенной этими газами при понижении их температуры от 380 до 20 оС при постоянном давлении.
= 853. Найти количество теплоты, выделенной этими газами при понижении их температуры от 380 до 20 оС при постоянном давлении.


