
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циклы газотурбинных установокСодержание книги
Поиск на нашем сайте
Газотурбинные установки (ГТУ) относятся к числу двигателей внутреннего сгорания. Газ, получившийся в результате сгорания топлива в камере сгорания, направляется в турбину. Продукты сгорания, расширяясь в сопловом аппарате и частично на рабочих лопатках турбины, производят на колесе турбины механическую работу. Газотурбинные установки, по сравнению с поршневыми двигателями, обладают целым рядом технико-экономических преимуществ: 1) простотой устройства силовой установки; 2) отсутствием поступательно движущихся частей; 3) бо′льшим числом оборотов, что позволяет существенно снизить вес и габариты установки; 4) бо′льшей мощностью одного агрегата; 5) возможностью осуществить цикл с полным расширением и тем самым с большим термическим кпд; 6) возможностью применения дешевых сортов топлива (керосина). Эти преимущества ГТУ способствовали ее распространению во многих областях техники и, особенно, в авиации. В основе работы ГТУ лежат идеальные циклы, состоящие из простейших термодинамических процессов. Термодинамическое изучение этих циклов базируется на следующих допущениях: · циклы обратимы; · подвод теплоты происходит без изменения химического состава рабочего тела цикла; · отвод теплоты предполагается обратимым; · гидравлические и тепловые потери отсутствуют; · рабочее тело представляет собой идеальный газ с постоянной теплоемкостью. К числу возможных идеальных циклов ГТУ относят следующие циклы: 1) с подводом теплоты при постоянном давлении р = const; 2) с подводом теплоты при постоянном объеме v = const; 3) с регенерацией теплоты. Во всех циклах ГТУ теплота при наличии полного расширения в турбине отводится при постоянном давлении. Цикл ГТУ с подводом теплоты при p = const (цикл Брайтона) Из перечисленных циклов наибольшее практическое применение получил цикл сподводом теплоты при р = const. В простейшей ГТУ со сгоранием топлива при постоянном давлении (рис. 9.19) компрессор 1, приводимый в движение газовой турбиной 4, подает сжатый воздух в камеру сгорания 3, в которую через форсунку впрыскивается жидкое топливо, подаваемое насосом 2, находящимся на валу турбины. Продукты сгорания расширяются в сопловом аппарате и частично на рабочих лопатках турбины и выбрасываются в атмосферу. При сделанных допущениях термодинамический цикл ГТУ со сгоранием при р = const можно изобразить на pv- и TS -диаграммах (рис. 9.20)ввиде площади acze. Работа цикла на р v -диаграмме представляет собой разность площадей 1 ez2 и 1ас2, соответственно равных работе турбины и компрессора.
Параметрами цикла являются степень повышения давления воздуха Термический КПД цикла определяют из общего выражения:
где
в точке с
в точке
в точке е
Найдем выражение для термического КПД цикла:
Выражение (9.13) показывает, что термический КПД ГТУ при данном рабочем теле и постоянном значении показателя адиабаты k зависит только от степени повышения давления в компрессоре, причем с ростом
Теоретическая работа цикла ГТУ:
где Взяв производную
Несмотря на то, что увеличение
При расчете высокотемпературных ГТУ необходимо учитывать переменные значения теплоемкости cp = f (T), энтальпии i = f (T),показателя адиабаты k = f (T) как в процессе расширения в турбине, так и в процессе сжатия, особенно в многоступенчатых компрессорах. Цикл ГТУ с подводом теплоты при v = const (цикл Гемфри) В газотурбинной установке, работающей по этому циклу, процесс сгорания происходит в замкнутом объеме камеры. В ГТУ со сгоранием при v = const (рис. 9.22) компрессор 1, приводимый во вращение турбиной 6, подает сжатый воздух в камеру сгорания 4 через управляемый клапан 7. Второй клапан 5 находится в конце камеры сгорания и предназначен для выхода продуктов сгорания на турбину. Топливо в камеру сгорания подается насосом 2, находящимся на валу турбины, через форсунку. Подача топлива должна осуществляться периодически топливным клапаном 3. В камере сгорания при закрытых клапанах 7 и 5 происходит процесс горения топлива в постоянном объеме. Приувеличении давления клапан 5 открывается, и продукты сгорания поступают в сопловой аппарат и на лопатки турбины 6. При прохождении через лопатки турбины газ совершает работу и выбрасывается в окружающую среду.
Для определения термического КПД, равного
найдем температуру газа в узловых точках цикла:
в точке
в точке е
Подставляя эти выражения для температур в формулу термического КПД, получим:
Эта формула показывает, что термический КПД цикла зависит от степени повышения давления Из сравнения между собой циклов с подводом теплоты при p = const и v = const на pv - и TS -диаграммах (рис. 9.25)видно, что при одной и той же степени повышения давления и одинаковом отводимом количестве теплоты цикл при v = const выгоднее цикла Это объясняется большей степенью расширения в цикле v = const, а следовательно, и большими значениями термического КПД. Несмотря на это преимущество, цикл с подводом теплоты при v = const широкого применения в практике не нашел в связи с усложнением конструкции камеры сгорания и ухудшением работы турбины в пульсирующем потоке газа, хотя работы по совершенствованию этого цикла продолжаются. Регенеративные циклы ГТУ
В установке с регенерацией (рис. 9.26) воздух из компрессора 1 направляется в теплообменник 3, где он получает теплоту от газов, вышедших из турбины 5. После подогрева воздух направляется в камеру сгорания 4, в которую через форсунку от насоса 2 подводится топливо. Воздух, уже нагретый отработавшими газами турбины, получает в камере сгорания меньшее количество теплоты для достижения определенной температуры газа перед турбиной. На pv - и TS -диаграммах цикла (рис. 9.27): а–с – адиабатное сжатие воздуха в компрессоре; с–1 – изобарный подогрев воздуха в регенераторе; 1– z – подвод теплоты при р = const в камере сгорания; z– e – адиабатное расширение газа в турбине; е–2 – отдача теплоты при р = const в регенераторе; 2–а – отдача теплоты при p= const в окружающую среду. Если предположить, что охлаждение газов в регенераторе происходит до температуры воздуха, поступающего в него с температурой Т2 = ТС,то регенерация будет полной. Термический КПД цикла при полной регенерации, когда Те – T 2 = T 1 – Тс,определяется по формуле:
где Тогда
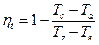 . .
При принятых параметрах цикла ГТУ с подводом теплоты при р = const
и
Последняя формула показывает, что термический КПД цикла при полной регенерации зависит как от начальной температуры, так и от температуры в конце адиабатного расширения. Обычно двигатели работают при не полной регенерации, поэтому Т2 > ТС. При этом термический КПД цикла должен учитывать степень регенерации, равную отношению количества теплоты, переданного воздуху, к тому количеству теплоты, которое могло бы быть передано при охлаждении газов до температуры сжатого воздуха.
где При полной регенерации: Т2 = ТС; T 1 = Te; при отсутствии регенерации: ТС = Т1; Степень регенерации зависит от качества и размеров площади рабочих поверхностей теплообменника (регенератора). Принципиально регенерацию теплоты можно осуществить и в ГТУ, работающей по циклу v = const. При этом характер цикла
Цикл Стирлинга
Одна из возможных конструктивных схем двигателя Стирлинга, когда рабочий 5 (рис. 9.29) и вытеснительный 1 поршни находятся в одном цилиндре. В процессе перекачки в горячую полость (над рабочим поршнем) рабочее тело в регенераторе 3 и нагревателе 4 получает теплоту, а в процессе перекачки в холодную полость (под рабочим поршнем) отдает теплоту в регенераторе 3 и охладителе 2. Для осуществления этих процессов движение вытеснительного поршня 1 сдвинуто по фазе по отношению к движению рабочего поршня 5. Идеальный цикл Стирлинга состоит из четырех процессов (рис. 9.30). Впроцессе а–с холодное рабочее тело сжимается в изотермическом процессе Та = Тс = Т2 при интенсивном отводе теплоты q 2 ". В процессе c– z поршень-вытеснитель перемещает рабочее тело из холодной полости в горячую, так что vc = vz (изохорный процесс), а температура увеличивается от ТС = Т2 до Tz = T 1 при подводе теплоты q 1 '.
Работа в цикле Стирлинга представляет собой разность работы, полученной в процессе изотермического расширения (подвод теплоты q 1 "),и работы, затраченной в процессе изотермического сжатия с отводом теплоты (q 2 "):
При полной регенерации
Термический КПД цикла при идеальном регенераторе равен:
Подставив выражения для q 1 " и q 2 " в уравнение (9.14), получим:
Так как изохоры идеального газа на TS -диаграмме эквидистантны, то
Следовательно:
Таким образом, термический КПД цикла Стирлинга с полной регенерацией теплоты равен термическому КПД цикла Карно. Если ввести параметры цикла:
Среднее давление цикла равно:
или
Двигатели Стирлинга завоевали право на широкое применение. Они достигли уровня современных дизелей, а по некоторым показателям превзошли их: · менее токсичны; · меньше уровень шума; · могут работать с практически любыми источниками теплоты. Так, был создан и испытан в космическом пространстве для привода регенератора двигатель Стирлинга, в котором в качестве источника теплоты использовалась энергия солнечных лучей. 9.12. Цикл воздушной холодильной машины. В холодильных установках происходит процесс передачи теплоты от охлаждающего тела к окружающей среде. Этот процесс осуществляется рабочим телом холодильной машины, так называемым холодильным агентом (хладоагентом). Эффективность цикла холодильной машины оценивается холодильным коэффициентом ( Холодильный коэффициент для 1 кг хладоагента, участвующего в цикле, равен:
Если осуществляется обратный цикл Карно в интервале температур Т1 – Т2,в ходе которого отбирается от холодильного источника теплота q 2 и передается источнику (окружающей среде) теплота q 1 , то имеем:
Формула (9.16) показывает, что Для определения работы и мощности, необходимой для осуществления обратного цикла, надо знать холодопроизводительность (Q) – количество теплоты, которое отводится от охлаждаемого тела в единицу времени:
где L – работа; Q – холодопроизводительность, Дж/с, N – мощность – кВт.
|
|||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.008 с.) |

 На этих диаграммах (рис. 9.20): а–с – процесс адиабатного сжатия воздуха в компрессоре; c- z – процесс подвода теплоты в камеру сгорания при p = const; z- e – адиабатный процесс расширения газа в турбине; е-а – изобарный процесс отдачи газом теплоты окружающему воздуху.
На этих диаграммах (рис. 9.20): а–с – процесс адиабатного сжатия воздуха в компрессоре; c- z – процесс подвода теплоты в камеру сгорания при p = const; z- e – адиабатный процесс расширения газа в турбине; е-а – изобарный процесс отдачи газом теплоты окружающему воздуху.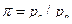 и степень предварительного расширения
и степень предварительного расширения 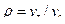 .
.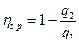 ,
,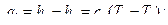
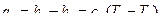 .
.
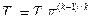 ;
;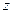
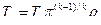 ;
;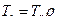 .
.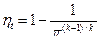 . (9.13)
. (9.13)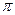 термический КПД цикла увеличивается.
термический КПД цикла увеличивается. На рис. 9.21 изображен рассматриваемый цикл при различных степенях повышения давления
На рис. 9.21 изображен рассматриваемый цикл при различных степенях повышения давления 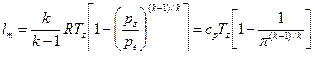 ;
;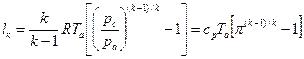 .
.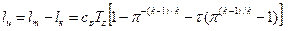 ,
,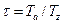 .
.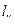 по
по 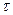 , найдем такое оптимальное значение
, найдем такое оптимальное значение 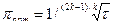 .
. В настоящее время максимально допустимая температура газов перед турбиной составляет 1100...1200 °С, и дальнейшее повышение температуры может быть достигнуто только при применении новых жаропрочных материалов и внедрении конструкций турбин с охлаждаемыми лопатками.
В настоящее время максимально допустимая температура газов перед турбиной составляет 1100...1200 °С, и дальнейшее повышение температуры может быть достигнуто только при применении новых жаропрочных материалов и внедрении конструкций турбин с охлаждаемыми лопатками.
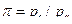 и степень изохорного повышения давления
и степень изохорного повышения давления 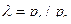 .
.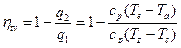 ,
, в точке с
в точке с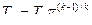 ;
;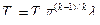 ;
;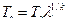 .
.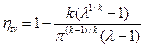 .
.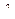 , характеризующей подведенное количество теплоты в цикле (рис. 9.24). Изменение
, характеризующей подведенное количество теплоты в цикле (рис. 9.24). Изменение 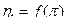 аналогично изменению термического КПД в цикле сподводом теплоты при p = const.
аналогично изменению термического КПД в цикле сподводом теплоты при p = const.
 Одной из мер повышения степени совершенства перехода теплоты в работу в ГТУ является применение регенерации теплоты. Регенерация теплоты заключается в использовании теплоты отработавших газов для подогрева воздуха, поступающего в камеру сгорания. Экономичность ГТУ при применении регенерации повышается.
Одной из мер повышения степени совершенства перехода теплоты в работу в ГТУ является применение регенерации теплоты. Регенерация теплоты заключается в использовании теплоты отработавших газов для подогрева воздуха, поступающего в камеру сгорания. Экономичность ГТУ при применении регенерации повышается.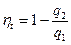 ,
,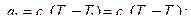
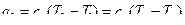 .
.
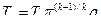 ;
; 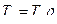
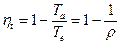 .
. При наличии регенерации теплоты термический КПД равен:
При наличии регенерации теплоты термический КПД равен: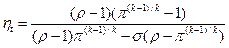 ,
,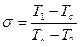 – степень регенерации.
– степень регенерации.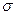 = 1;
= 1; Двигатель Стирлинга – газовый двигатель поршневого типа с внешним подводом теплоты, которая получается в результате сгорания твердых, жидких, газообразных топлив. Внешний подвод теплоты осуществляется через теплопроводящую стенку. Рабочее тело (водород, гелий, аргон, углекислый газ) находится в замкнутом пространстве и во время работы не заменяется.
Двигатель Стирлинга – газовый двигатель поршневого типа с внешним подводом теплоты, которая получается в результате сгорания твердых, жидких, газообразных топлив. Внешний подвод теплоты осуществляется через теплопроводящую стенку. Рабочее тело (водород, гелий, аргон, углекислый газ) находится в замкнутом пространстве и во время работы не заменяется.
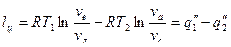 .
.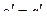 , так как
, так как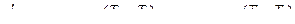 ;
;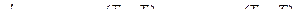 .
.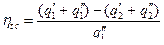 . (9.14)
. (9.14)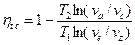 .
.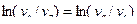 .
.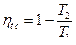 .
.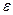 = va / vc – степень сжатия и
= va / vc – степень сжатия и 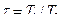 – степень повышения температуры, то термический КПД цикла может быть преобразован к виду:
– степень повышения температуры, то термический КПД цикла может быть преобразован к виду: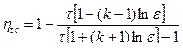 .
.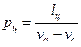
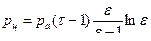 .
.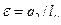 . (9.15)
. (9.15)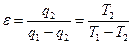 . (9.16)
. (9.16)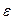 зависит от температуры Т2 и температуры окружающей среды (Т1). Можно доказать, что холодильный коэффициент цикла Карно не будет зависеть от выбора рабочего тела цикла.
зависит от температуры Т2 и температуры окружающей среды (Т1). Можно доказать, что холодильный коэффициент цикла Карно не будет зависеть от выбора рабочего тела цикла.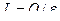 ;
;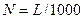 ,
,


