
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл Карно и его термодинамическое значениеСодержание книги
Поиск на нашем сайте
Французский инженер Сади Карно в 1824 г. предложил цикл идеального теплового двигателя, который служит эталоном для оценки совершенства идеальных циклов, так как он имеет максимальное значение термического коэффициента полезного действия (КПД) в системе, имеющей два изотермических источника теплоты. Прямой цикл Карно Прямой цикл Карно можно представить следующим образом. Существует два источника теплоты с более высокой температурой (Т1)и источник с более низкой температурой (Т2), причем Т1 = const и Т2 = const, так как предполагается, что источники теплоты обладают большим количеством энергии, и поэтому некоторое количество подведенной или отведенной теплоты не изменяет их температуры. Рассмотрим процессы прямого цикла Карно для 1 кг идеального газа в pv -диаграмме (рис. 9.3).
Затем рабочее тело начинает сжиматься при взаимодействии с источником с более низкой температурой, от него отводится теплота q 2. Происходит изотермическое сжатие по линии 3–4. В точке 4 рабочее тело опять изолируется от источника теплоты, и дальнейшее сжатие и возвращение рабочего тела в первоначальное состояние идет по адиабате 4–1 с повышением температуры. Цикл замыкается. Найдем термический КПД цикла Карно. Поскольку процессы 1–2 и 3–4 изотермические, то можно записать:
следовательно:
Для адиабатных процессов 2–3 и 4–1 справедливы следующие уравнения:
или
Окончательно получим:
Обратный цикл Карно Из точки 1 (рис. 9.4) рабочее тело с параметрами p 1, v 1, T 1 адиабатно расширяется до состояния 2 и соединяется с источником низкой температуры. Дальнейшее расширение (2–3) идет с подводом теплоты q 2 к рабочему телу. Протекает процесс изотермического расширения. В точке 3 рабочее тело вновь изолируется от источника теплоты и в процессе 3–4 адиабатно сжимается с повышением температуры от Т2 до Т1. В точке 4 рабочее тело соединяется с источником высокой температуры, и дальнейшее сжатие происходит по изотерме 4–1 с отводом теплоты q 1 к высокотемпературному источнику. Рабочее тело возвращается в свое первоначальное состояние и цикл замыкается. Холодильный коэффициент обратного цикла Карно определяется следующим образом:
Регенеративный цикл
Регенеративный цикл (рис. 9.5), состоящий из двух изотерм 4–1 и 2–3 и двух политроп 1–2 и 3–4, протекает следующим образом. По верхней изотерме 4–1к рабочему телу массой 1 кг подводится удельная теплота q 1. От точки 1 начинается процесс расширения, но он идет не по адиабате 1–5, как он шел бы в цикле Карно, а по некоторой политропе 1–2 сотводом теплоты регенерации qp. Точка 2 располагается на диаграмме левее точки 5, так как вследствие отвода теплоты в процессе 1–2 удельная энтропия рабочего тела уменьшается. По нижней изотерме 2–3теплота q 2 отводится в теплоприемник. От точки 3 начинается процесс сжатия по некоторой политропе 3–4с подводом теплоты q р. Поскольку вся теплота qp, отбираемая в процессе 1–2, подводится в процессе 3–4, то можно рассматривать линию 1–2 как линию 3–4,передвинутую вправо, а заштрихованные на рисунке площади, определяющие одну и ту же теплоту q р, считать одинаковыми. Это значит, что если одну из этих площадей наложить па другую, то они полностью совпадут, и получится цикл Карно 1–5–6–4. Следует отметить, что теплота q р в установке не расходуется, ее нужно затратить только один раз при пуске установки в ход. Следовательно, термический КПД рассматриваемого цикла 1–2–3–4 можно считать равным отношению пл. 1564 к пл. 4197, как и для термического КПД цикла Карно, совершаемого в тех же температурных границах, что и цикл 1–2–3–4. В связи с этим регенеративный цикл называется также обобщенным циклом Карно. 9.4. Основные процессы в одноступенчатом Компрессоры и детандеры (турбины) являются важнейшими частями энергетических установок, и от степени их совершенства зависит в целом и КПД установки. Назначение компрессора состоит в сжатии газа и непрерывной подаче его потребителю. Сжатый газ находит широкое применение в технике, в частности в авиации. Компрессор является одним из основных агрегатов газотурбинных, поршневых и комбинированных авиационных двигателей. В поршневых двигателях сжатие воздуха происходит в цилиндрах. Если двигатель комбинированный, то сжатие воздуха или топливовоздушной смеси (наддув двигателя) предварительно осуществляется в компрессоре. По способу сжатия воздуха или газа компрессоры можно разделить на две группы: · к первой относятся объемные компрессоры (поршневые, шестеренчатые, ротационные).Давление в них повышается при непосредственном уменьшении объема газа, поступившего в рабочее пространство компрессора; · ко второй группе относятся центробежные, осевые и диагональные компрессоры,последние из которых по своим характеристикам является промежуточными между центробежными и осевыми компрессорами. Во всех этих компрессорах сжатие осуществляется как бы в два этапа. На первом этапе газ получает некоторую скорость, приобретает кинетическую энергию. На втором происходит преобразование кинетической энергии в потенциальную энергию давления. Несмотря на конструктивные различия компрессоров термодинамические процессы сжатия, происходящие в них, одинаковы. Поэтому термодинамические основы процессов сжатия газа или воздуха рассмотрим применительно к поршневому компрессору как наиболее простому.
При ходе поршня вправо открывается всасывающий клапан 3, и в цилиндр при неизменном давлении поступает газ. При обратном ходе поршня и закрытых клапанах этот газ сжимается. После того как в результате сжатия будет достигнуто заданное давление, открывается нагнетательный клапан 4, и при движении поршня справа налево происходит выталкивание сжатого газа (при постоянном давлении) к потребителю. В поршневом компрессоре не весь объем, соответствующий одному ходу поршня, может быть использован для всасывания новой порции газа за счет так называемого вредного пространства, которое остается между поршнем и головкой цилиндра, когда поршень находится в крайнем (ближнем к головке) положении. В идеальном поршневом компрессоре вредным пространством и, как следствие, расширением газа перед процессом всасывания, пренебрегают. Рабочая диаграмма компрессора в координатах р – V имеет вид (рис. 9.7, а), где Так как процессы А – В и C – D не являются термодинамическими и идут с неизменными параметрами, то совокупность процессов, изображенных на рис. 9.7, а, не является замкнутым термодинамическим процессом (циклом).
пл. ABCD = пл. CDOE + пл. BCEF – пл. ABFO, где пл. CDOE = пл. BCEF = пл. ABFO = Значение работы, затрачиваемой на сжатие, всегда отрицательно (v 1 > v 2, dv < 0). Отрицательна и работа выталкивания, так как в процессе выталкивания работа производится над газом. Наконец, работа в процессе всасывания положительна, так как в этом случае поступающий газ совершает (отдает) работу. Следовательно, суммарная работа равна:
Эта работа является технической работой процесса сжатия.
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.210 (0.007 с.) |

 Предположим, что в цилиндре под поршнем находится 1 кг идеального газа с параметрами p 1, v 1, T 1 (точка 1). В этом состоянии к рабочему телу подводится от источника с более высокой температурой некоторое количество теплоты q 1, в результате чего осуществляется процесс изотермического расширения. В точке 2 рабочее тело имеет параметры p 2, v 2, T 1. В этой точке рабочее тело изолируется от источника теплоты. Поэтому дальнейшее расширение протекает адиабатно. В конце адиабатного расширения (точка 3) рабочее тело имеет параметры p 3, v 3, T 2.
Предположим, что в цилиндре под поршнем находится 1 кг идеального газа с параметрами p 1, v 1, T 1 (точка 1). В этом состоянии к рабочему телу подводится от источника с более высокой температурой некоторое количество теплоты q 1, в результате чего осуществляется процесс изотермического расширения. В точке 2 рабочее тело имеет параметры p 2, v 2, T 1. В этой точке рабочее тело изолируется от источника теплоты. Поэтому дальнейшее расширение протекает адиабатно. В конце адиабатного расширения (точка 3) рабочее тело имеет параметры p 3, v 3, T 2.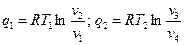 ,
,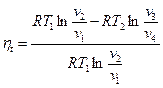 .
.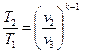 и
и 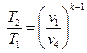 .
.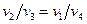
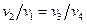 .
.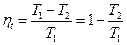 .
.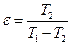 .
. Одноцилиндровый поршневой компрессор (рис. 9.6) состоит из цилиндра 1 с поршнем 2,который движется возвратно-поступательно, и двух клапанов: всасывающего 3 и нагнетающего 4.
Одноцилиндровый поршневой компрессор (рис. 9.6) состоит из цилиндра 1 с поршнем 2,который движется возвратно-поступательно, и двух клапанов: всасывающего 3 и нагнетающего 4.
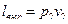 – работа выталкивания;
– работа выталкивания;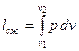 – работа сжатия;
– работа сжатия;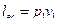 – работа всасывания.
– работа всасывания.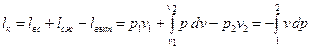 . (9.1)
. (9.1)


