
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность при стационарном режимеСодержание книги
Поиск на нашем сайте
Дифференциальное уравнение теплопроводности при стационарном режиме без внутренних источников теплоты имеет вид:
Для решения конкретной задачи к этому уравнению надо присовокупить соответствующие граничные условия. Рассмотрим несколько простейших случаев определения стационарного поля температур в телах различной формы. Плоская стенка Рассмотрим неограниченную тонкую стенку толщиной Пусть на поверхностях стенки поддерживаются соответственно температуры
При отыскании распределения поля температур используем граничные условия:
После первого интегрирования имеем:
После второго интегрирования имеем:
Постоянные
из второго граничного условия определим константу
откуда
Таким образом, решением уравнения (10.2) будет выражение:
т.е. функция T(x) линейно зависит от x.
или в данном случае:
Определим количество теплоты потока через стенку в единицу времени:
где F – площадь стенки. Теперь определим плотность теплового потока через трехслойную стенку (рис. 10.6). Для каждого слоя можно записать следующие выражения: для первого слоя
для второго слоя
для третьего слоя
Из уравнений (10.3) – (10.5) можно найти термическое сопротивление трехслойной стенки. Для этого сначала определим местные температурные напоры на каждой стенке:
Почленно сложив эти уравнения, получим:
откуда
На основании последнего выражения для многослойной стенки получим:
где n – количество слоев. С вводом обозначения
где
Цилиндрическая стенка Запишем дифференциальное уравнение теплопроводности в цилиндрической системе координат. Для этого используем известные соотношения, связывающие декартовы и цилиндрические координаты (рис. 10.7): Тогда
Рассмотрим одномерный процесс теплопроводности в бесконечной цилиндрической стенке (рис. 10.8). Предположим, что на внутренней и внешней полостях стенки, температура не зависит от угла
Зададим граничные условия задачи:
Приведем уравнение (10.8) к виду:
откуда
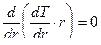 . .
После первого интегрирования получим:
После второго интегрирования имеем:
Постоянные интегрирования определим из граничных условий: при при Вычитая из уравнения(10.11) выражение (10.10) получим:
следовательно,
Постоянную
Подставляя выражения для
или
Из последнего выражения видно, что искомое распределение температуры по толщине цилиндрической стенки логарифмически зависит от координаты r. Плотность теплового потока
Количество теплоты, проходящее сквозь цилиндрическую стенку, через единицу длины:
Используя последнюю формулу можно определить количество теплоты, проходящее сквозь многослойную цилиндрическую стенку:
где n – количество слоев.
|
|||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.111 (0.006 с.) |

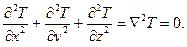
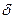 (рис. 10.5).
(рис. 10.5).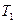 и
и 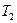 . Если
. Если  не зависят от z и y, то очевидно, искомое температурное поле тоже не будет зависеть от этих координат и тогда:
не зависят от z и y, то очевидно, искомое температурное поле тоже не будет зависеть от этих координат и тогда: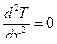 . (10.2)
. (10.2)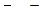 при
при 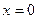
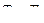 при
при 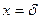
 Представим выражение (10.2) в виде:
Представим выражение (10.2) в виде: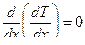 .
.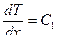 или
или  .
.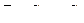 .
. и
и  определим из граничных условий. Из первого граничного условия имеем:
определим из граничных условий. Из первого граничного условия имеем: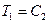 ;
;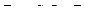 ,
,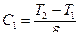 .
.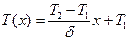 ,
, Найдем плотность теплового потока. Согласно закону Фурье:
Найдем плотность теплового потока. Согласно закону Фурье: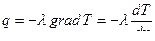
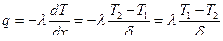 .
.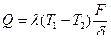 ,
,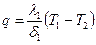 ; (10.3)
; (10.3)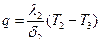 ; (10.4)
; (10.4)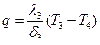 . (10.5)
. (10.5)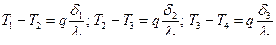 .
.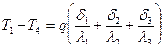 ,
,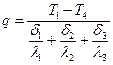 .
.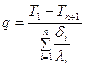 , (10.6)
, (10.6)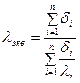 , (10.7)
, (10.7)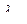 – эквивалентная теплопроводность, выражение (10.6) можно представить в виде:
– эквивалентная теплопроводность, выражение (10.6) можно представить в виде: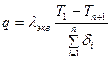 .
.
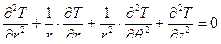 .
.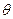 . Тогда получим:
. Тогда получим: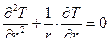 . (10.8)
. (10.8) при
при  ;
; .
.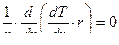

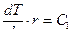 или
или 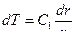 .
.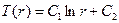 . (10.9)
. (10.9)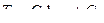 ; (10.10)
; (10.10)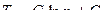 . (10.11)
. (10.11)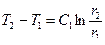 ,
,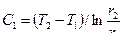 .
.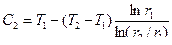 .
.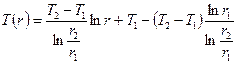
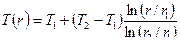 .
.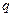 определим из закона Фурье:
определим из закона Фурье: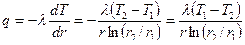 .
.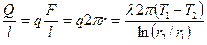 .
.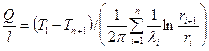 ,
,


