
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл воздушной холодильной машиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основными элементами установки для получения холода (рис. 9.31) являются компрессор 3 и детандер 1. Кроме них имеются два теплообменных аппарата, в одном из них – рефрижераторе 4 воздух воспринимает теплоту от охлаждаемой емкости, а во втором – холодильнике 2 отдает теплоту окружающей среде или воде холодильника. Процессы в холодильнике и рефрижераторе идут при постоянном давлении, если пренебречь гидравлическими сопротивлениями. В компрессоре давление повышается от p 1 до р2,в детандере падает от р2 до р1,причем процессы сжатия и расширения считают адиабатными. Таким образом, идеализированный цикл холодильной машины
Количество теплоты, отдаваемое воздухом в окружающую среду (охлаждающей воде) в изобарном процессе 4–1, равно:
Считая воздух идеальным газом с постоянной теплоемкостью, найдем:
Тогда работа, необходимая для осуществления цикла, равна:
Подставляя выражения для q 2 и l ц в формулу (9.15), получим:
или
Для адиабатного процесса 3–4 можно записать:
и аналогично для адиабатного процесса 1–2
Тогда уравнение (9.17) можно переписать в виде:
или
Таким образом, холодильный коэффициент цикла зависит только от отношения давлений р1/р2. При постоянных температурах окружающей среды и охлаждаемой емкости рассматриваемый цикл является внешне необратимым. Это вызвано тем, что изобарные процессы теплообмена протекают при конечной разности температур, поэтому холодильный коэффициент этого цикла, по сравнению с холодильным коэффициентом цикла Карно меньше. Из рис. 9.33 видно, что в обратном цикле Карно отбирается теплоты больше, чем в цикле Лоренца: пл. 1'3 ba1' > пл. 23 bа2, а работа, затрачиваемая и цикле воздушной холодильной установки, больше, чем в обратном цикле Карно: пл. 12341> пл. 11'33'1. Цикл теплового насоса Тепловым насосом называется специальное устройство для отопления помещений. По принципу действия тепловой нacoc может быть отнесен к холодильным машинам, так как он, как и эти машины, переносит теплоту в цикле с нижнего температурного уровня на верхний с затратой для этого внешней работы в соответствии со вторым началом термодинамики. Следовательно, цикл теплового насоса – это обратный цикл, как и циклы холодильных машин.
Цель работы теплового насоса другая. Он должен поддерживать в помещении тоже постоянную, но более высокую температуру, чем Т0,за счет отбора теплоты из окружающей среды. Эту теплоту тепловой насос переносит на более высокий температурный уровень, соответствующий температуре в помещении, где она воспринимается водой, циркулирующей в отопительной системе. Таким образом, компенсируется самопроизвольный переход теплоты из отапливаемого помещения в окружающую среду. В тепловом насосе (рис. 9.34) имеется испаритель1, в котором происходит превращение конденсата холодильного агента в парообразное состояние. В этом процессе к конденсату подводится теплота из окружающей среды. Такой средой в данном случае является вода, забираемая из водоема и прокачиваемая через испаритель насосом 2. Получившийся в испарителе пар хладоагента отводится в компрессор 6, где он сжимается с повышением температуры, после чего направляется в конденсатор 3. Здесь пар конденсируется, а выделившаяся при этом теплота воспринимается водой, циркулирующей в отопительной системе 5, обогревающей помещение 4. Конденсат же, пройдя через редукционный вентиль 7 для понижения давления, поступает в испаритель. Эффективность теплового насоса оценивается отопительным коэффициентом:
где q 1 – количество теплоты, сообщаемое нагреваемому объекту; l ц – работа, подводимая к рабочему телу в цикле. Если в целях отопления используют определенную холодильную машину с холодильным коэффициентом
Следовательно, чем выше холодильный коэффициент, тем выше и отопительный коэффициент. Так как в тепловом насосе Если бы тепловой насос работал по циклу Карно, то с учетом формул (9.16) и (9.20)
При постоянной температуре нижнего источника теплоты (Т2) эффективность теплового насоса будет зависеть от температуры, при которой рабочее тело отдает теплоту в отопительную систему. Этой температурой и нужно руководствоваться при выборе теплоносителя. Примеры решения задач Пример 9.1 Найти максимально допустимое давление сжатия в идеальном одноступенчатом воздушном компрессоре (р2), если температура самовоспламенения смазочного масла Решение Максимально допустимую температуру воздуха в конце сжатия принимаем равной температуре самовоспламенения масла: T2 = tм + 273 = 270 + 273 = 543 К. Температуру воздуха в начале сжатия примем равной температуре наружного воздуха Тв = 300 К. Максимально допустимое конечное давление воздуха равно:
Из этого примера следует, что для бескомпрессорных дизелей, требующих применения пускового воздуха давлением порядка 3 МПа, одноступенчатый пусковой компрессор непригоден. Пример 9.2 Объемная подача идеального одноступенчатого воздушного компрессора составляет 0,2 м3/с при температуре всасывания 27° С и давлении 0,1 МПа. Давление сжатого воздуха 0,8 МПа. Найти температуру воздуха и объемную подачу компрессора (по конечным параметрам воздуха) в конце сжатия и мощность, затрачиваемую на получение сжатого воздуха, в трех вариантах: 1) при сжатии по изотерме; 2) по адиабате (k = 1,4); 3) и по политропе (п = 1,2). Решение 1) При изотермическом сжатии Абсолютная температура равна: T2 = T1= 27 + 273 = 300 К. Объемная подача по конечным параметрам равна:
Последнее выражение получено с учетом того, что Мощность при изотермическом сжатии определим по уравнению (9.6), с учетом формул (9.2), (9.7) и того, что
2) При адиабатном сжатии Конечная температура воздуха равна:
Объемная подача по конечным параметрам:
Мощность при адиабатном сжатии определим из совместного рассмотрения уравнений (9.6), (9.3) и (9.7). Так же, как и в первом случае, учитываем, что
3) При политропном сжатии Конечная температура воздуха:
Объемная подача по конечным параметрам:
Выражение для определения мощности при политропном сжатии определяется аналогично, как и для случая адиабатного сжатия. Только вместо уравнения (9.3) будем использовать выражение (9.5). Получим:
Пример 9.3 Исследовать термодинамический цикл ДВС со смешанным подводом теплоты по следующим данным: ра = 0,1 МПа; ta = 27° С; cv = 0,72 кДж/(кг К); k = 1,4; Решение Находим параметры в характерных точках цикла (см. рис. 9.14).: В точке а – начале сжатия
Для воздуха R = 287,1 Дж/(кг·К); Та = 273 + ta = 273 + 27 = 300 К, поэтому va = 287,1 · 300 / (0,1·106) = 0,861 м3/кг; В точке с – конце сжатия
откуда
или tc = 610 °С. В точке степень повышения давления:
или
В точке z – конце подвода теплоты при постоянном давлении Предварительно вычисляем
поэтому
Температуру
отсюда
Находим предварительно cp:
Подставляя значение cp, определяем:
или tz = 2274 - 273 = 2001 °С. Найдем vz. Сначала подсчитаем степень предварительного расширения:
Теперь вычисляем vz:
В точке е – конце адиабатного расширения
находим
или t е = 1034 – 273 = 761 °С. Давление в искомой точке цикла:
Определим термический КПД цикла по уравнению (9.9):
= 0,605 (60,5 %). 9.14. Задачи для самостоятельного решения 9.1. Компрессор, имеющий подачу 100 м3/ч, подает охлажденный до начальной температуры сжатый воздух давлением 0,5 МПа. Наружное давление 0,1 МПа при температуре 27 °С. Найти подводимую теоретическую мощность при: а) изотермическом сжатии; б) политропном сжатии (n = 1,25); в) адиабатном сжатии (k = 1,4). Ответ:а) 21,9 кВт; б) 25,9 кВт; в) 27,9 кВт. 9.2. Компрессор всасывает воздух объемом 500 м3/ч, давлением 0,1 МПа и температурой 17° С. В компрессоре воздух изотермически сжимается до давления 0,9 МПа.Определить объем цилиндра компрессора и теоретическую подводимую к нему мощность, если частота вращения вала компрессора 100 мин -1. Ответ: Vh = 83,3л; NT = 29,9 кВт. 9.3. Воздушный компрессор всасывает воздух объемом 500 м3/ч, давлением Ответ: Т2 = 543 К; Vh = 83,3 л; NT = 41,6 кВт. 9.4. Компрессор подает воздух массой 500 кг/ч, охлажденный до начальной температуры и сжатый до 0,8 МПа. Давление в цилиндре компрессора в начале сжатия Ответ:экономия составила 3,46 кВт, или 10,5 %. 9.5. Известны следующие параметры цикла со смешанным подводом теплоты и его характеристики: ра = 0,1 МПа, ta = 30 °С степень сжатия ε = 7, степень повышения давления λ = 2,0, степень предварительного расширения ρ = 1,2, рабочее тело – воздух. Найти параметры характерных точек диаграммы цикла, количество подведенной теплоты, удельную работу цикла и его термический КПД. Ответ: va =0,870 м3/кг; vc = 0,124 м3/кг; vz = 0,149 м3/кг; рс = 1,52 МПа; р z = 3,05 МПа; ре = 0,26 МПа; tc = 387 °С; q 1 = 744,2 кДж/кг; q 2 =378,2 кДж/кг; l ц = 396 кДж/кг; 9.6. Для цикла со смешанным подводом теплоты дано: рабочее тело – воздух; Найти Ответ: 9.7. Найти давление и температуры в точках а, с, z', z и e цикла со смешанным подводом теплоты и Ответ: 9.8. Для цикла с изохорным подводом теплоты, совершаемого воздухом, масса которого 1 кг, заданы следующие параметры: ра =0,1 МПа, ta = 27° С. Определить подведенную удельную теплоту (q 1), удельную работу цикла (l ц)и термический КПД ( Ответ: q 1 = 1,29 МДж/кг; l ц = 628 кДж/кг; 9.9. Исследовать цикл с изохорным подводом теплоты, совершаемый воздухом массой 1 кг, если дано: ра = 0,1 МПа; ta = 27 °С; ε = 5,5; cv = 0,722 кДж/(кг·К); Ответ: va = 0,88 м3/кг; vz = 0,16 м3/кг; р z = 3,87 МПа; Tz = 2160 K; Тс = 592 К; 9.10. Определить степень сжатия и термический КПД цикла с изохорным подводом теплоты при следующих данных: ta = 60 °С, t с = 270 °С и k =1,4. Ответ: ε = 3,4; Теплопередача
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.008 с.) |

 Особенность воздушных холодильных машин состоит в том, что воздух, имея малую теплоемкость, обеспечивает сравнительно небольшую холодильную мощность, а поэтому для нормальной работы установки требуются большие массовые расходы воздуха.
Особенность воздушных холодильных машин состоит в том, что воздух, имея малую теплоемкость, обеспечивает сравнительно небольшую холодильную мощность, а поэтому для нормальной работы установки требуются большие массовые расходы воздуха.
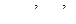 .
.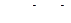 .
.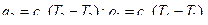 .
. .
.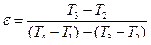
 . (9.17)
. (9.17)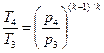 (9.18)
(9.18)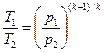 . (9.19)
. (9.19) Так как для изобарных процессов 4–1 и 2–3 p 1 = p 4 и р2 = р3, то из уравнений (9.18) и (9.19) имеем:
Так как для изобарных процессов 4–1 и 2–3 p 1 = p 4 и р2 = р3, то из уравнений (9.18) и (9.19) имеем: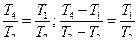 .
.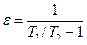
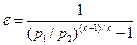 .
. Однако используются холодильные машины и тепловой насос для разных целей. Цель работы холодильных машин состоит в том, чтобы поддерживать в холодильной камере постоянную и при том более низкую температуру, чем температура окружающей среды (Т 0).Для этого холодильные машины должны отводить из этой камеры теплоту, самопроизвольно проникающую в нее (несмотря на изоляцию) из внешней среды, и затем отводить эту теплоту в окружающую же среду, но при более высокой температуре.
Однако используются холодильные машины и тепловой насос для разных целей. Цель работы холодильных машин состоит в том, чтобы поддерживать в холодильной камере постоянную и при том более низкую температуру, чем температура окружающей среды (Т 0).Для этого холодильные машины должны отводить из этой камеры теплоту, самопроизвольно проникающую в нее (несмотря на изоляцию) из внешней среды, и затем отводить эту теплоту в окружающую же среду, но при более высокой температуре. ,
,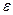 , то
, то  . Тогда
. Тогда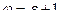 . (9.20)
. (9.20)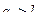 , то и
, то и  > 1. Значение отопительного коэффициента в реальных тепловых насосах равно 3... 5.
> 1. Значение отопительного коэффициента в реальных тепловых насосах равно 3... 5.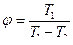 .
.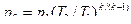 = 0,1·106·(543 / 300)1,4/(1,4-1) = 0,798 МПа.
= 0,1·106·(543 / 300)1,4/(1,4-1) = 0,798 МПа.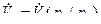 = 0,2·(0,1·106 / 0,8·106) = 0,025 м3/с.
= 0,2·(0,1·106 / 0,8·106) = 0,025 м3/с.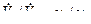 .
. :
: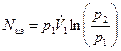 /1000=0,1·106·0,2·ln 8 / 1000=41,5 кВт.
/1000=0,1·106·0,2·ln 8 / 1000=41,5 кВт.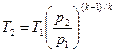 = 300·8(1,4-1)/1,4 = 544 К.
= 300·8(1,4-1)/1,4 = 544 К.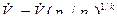 = 0,2·(1 / 8)1/1,4 = 0,045 м3/с.
= 0,2·(1 / 8)1/1,4 = 0,045 м3/с.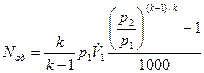 = 1,4 / (1,4 - 1)·0,1·106 ·0,2·[8(1,4-1)/1,4 - 1] / 1000 = 56,7 кВт.
= 1,4 / (1,4 - 1)·0,1·106 ·0,2·[8(1,4-1)/1,4 - 1] / 1000 = 56,7 кВт.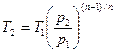 = 300·8(1,2-1)/1,2 = 368 К.
= 300·8(1,2-1)/1,2 = 368 К. = 0,2·(1/8)1/1,2 = 0,033 м3/с.
= 0,2·(1/8)1/1,2 = 0,033 м3/с.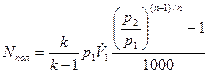 = 1,4 / (1,4 - 1)·0,1·106 ·0,2·[8(1,2-1)/1,2 - 1] / 1000 = 49,8 кВт.
= 1,4 / (1,4 - 1)·0,1·106 ·0,2·[8(1,2-1)/1,2 - 1] / 1000 = 49,8 кВт. +
+  = 1340 кДж/кг;
= 1340 кДж/кг;  = 5,5 МПа и ε = 15. Рабочее тело – воздух, рассматриваемый как идеальный газ. Масса воздуха 1 кг.
= 5,5 МПа и ε = 15. Рабочее тело – воздух, рассматриваемый как идеальный газ. Масса воздуха 1 кг.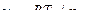 .
.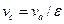 = 0,861 / 15 = 0,0573 м3/кг;
= 0,861 / 15 = 0,0573 м3/кг;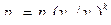 ,
,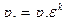 = 0,1·151,4 = 4,43 МПа;
= 0,1·151,4 = 4,43 МПа; = 4,43·106 ·0,0573 / 287,1 = 883 К
= 4,43·106 ·0,0573 / 287,1 = 883 К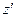 – конце подвода теплоты при постоянном объеме
– конце подвода теплоты при постоянном объеме = 5,5 / 4,43 = 1,242;
= 5,5 / 4,43 = 1,242;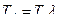 = 883 · 1,242 = 1097 К
= 883 · 1,242 = 1097 К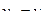 = 0,0573 м3/кг.
= 0,0573 м3/кг.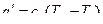 = 0,72·106·(1097 – 883) = 154 кДж/кг,
= 0,72·106·(1097 – 883) = 154 кДж/кг,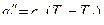 ,
,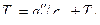 .
.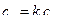 = 1,4·072·103 = 1,01 кДж/(кг·К).
= 1,4·072·103 = 1,01 кДж/(кг·К).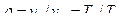 = 2274 / 1097 = 2,07.
= 2274 / 1097 = 2,07.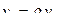 = 2,07 · 0,0573 = 0,118 м3/кг.
= 2,07 · 0,0573 = 0,118 м3/кг.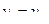 = 0,861 м3/кг;
= 0,861 м3/кг;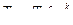 = 300 · 1,242 · 2,071,4 = 1034 К
= 300 · 1,242 · 2,071,4 = 1034 К = 0,1 · 1,242 · 2,071,4 = 0,344 МПа.
= 0,1 · 1,242 · 2,071,4 = 0,344 МПа. =
=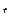 =1311 °С; t е = 511 °С;
=1311 °С; t е = 511 °С;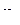 = 0,532.
= 0,532. .
.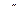 = 911,4 кДж/кг; l ц = 741 кДж/кг;
= 911,4 кДж/кг; l ц = 741 кДж/кг; 


