Тема: Построение эпюр поперечных сил и изгибающих моментов по длине балки

Время выполнения работы – 3часа

Цель: Для балки, лежащей на двух опорах и нагруженной сосредоточенными силами F₁ и F₂, и парой сил с моментом М. Определить реакции опор и построить эпюры изгибающих моментов поперечных сил. Данные для своего варианта взять в таблице 1.

Порядок выполнения практической работы:

1. Составить уравнение равновесия;

2. Найти реакции опор;

3. Сделать проверку правильности определения реакций опор;

4. Построить эпюру – Q;

5. Построить эпюру – М;

6. Определить опасное сечение балки по эпюре изгибающих моментов – М;

7. Проверить условие прочности балки;

8. Подобрать сечение балки стальной двутавровой в соответствии с ГОСТ.

Дано: Для двухопорной балки построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать сечение стального двутавра, приняв [δи]=160 МПа.

F₁=24 кН; F₂=36 кН; m₁=18 кНм; m₂=24 кНм; L₁=2,0 м; L₂=3,0 м; L₃=3,0 м.

 

 

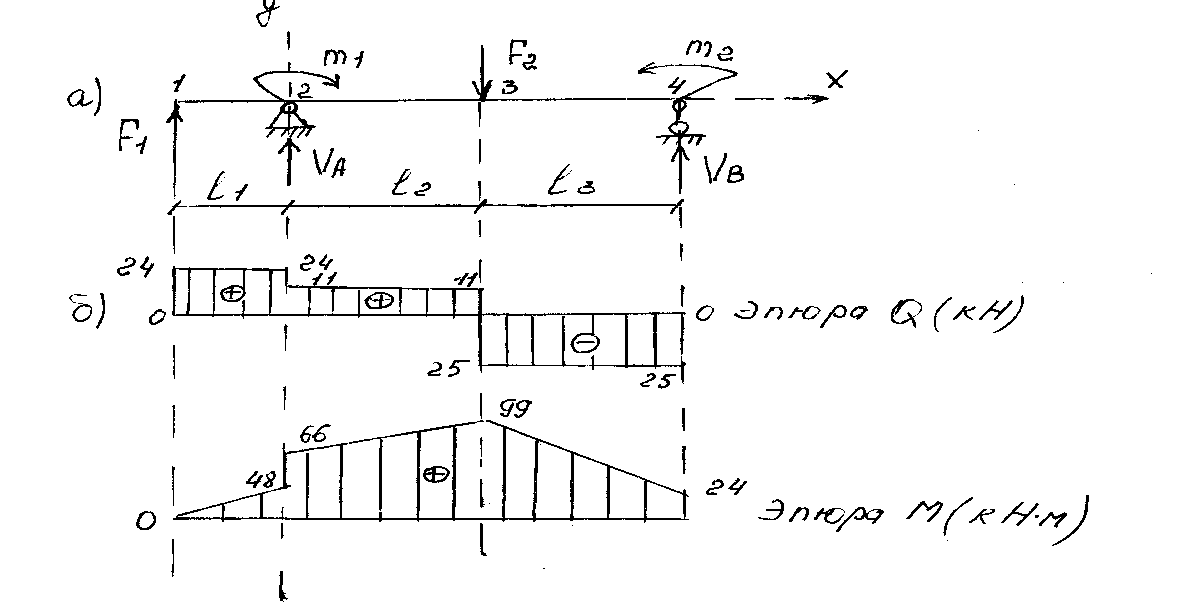
Рисунок 1- Построение эпюры Q иM.

 

Решение:

1. Составляем уравнения равновесия плоской системы произвольно расположенных сил, из которых определяем опорные реакции балки:

∑М_А(F_R)= F₁ ∙ 2,0 + m₁ +F₂∙3,0 – m₂-Vв∙6,0 =0, (1)

 

∑ Мв(F_R)= F₁∙8,0+m₁+V_А∙6,0- F₂∙3,0-m₂=0, (2)

 

Из уравнения (2) находим Va:

 

V_А = (-F₁∙8,0- m₁+F₂∙3,0+ m₂) /6,0=(-192-18+108+24) /6,0= - 13кН,
Из уравнения (1) находим Vв:

 

V_в= (F₁∙2,0+ m₁+ F₂ ∙3,0- m₂) /6,0=(48+18+108-24) /6,0=150/6=25кН,

 

Проверяем правильность опорных реакций, составляя сумму проекций всех сил на ось Y:
∑F_RУ= F₁ + V_А - F₂+ Vв=24-13-36+25=49-49=0,
т.е. реакции определены верно.

 

2. Определяем значение поперечной силы - Q в характерных сечениях балки, которая обозначена цифрами 1,2,3,4 (рисунок-2а).

Q ₁= Q ₂^лев=F₁=24 кН,
Q ₂^прав= Q ₃^лев = F₁+ V_А =24-13=11 кН,

Q ₃^прав= Q ₄= F_{1 +} V_А - F₂= -Vв= - 25 кН.

По найденным значениям строим эпюру поперечных сил - Q (рисунок-1б).

 

2. Аналогично определяем значения изгибающего момента - М в характерных сечениях балки:

М ₁=0;

М ₂^лев= F₁∙2,0 = 48 кНм,
М ₂^прав=м₂^лев+ m₁ =48+18=66 кНм,

М₃ = F₁ ∙5,0+ m₁+ V_А ∙3,0=120+18-39=99 кНм,

М₄ = m₂=24 кНм.

 

По найденным значениям строим эпюру изгибающих моментов -М (рисунок-. 1в).

 

2. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечение, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае - это сечение 3, где

Мз=Мmах=99 кНм.

 

Из условия прочности балки на изгиб:

δ= М mах <[δи],

Wх

Wх = М mах=99∙10⁶Н∙мм = 0,619∙ 10⁶ мм ³ =619см³, [δи] 160 Н/мм²

 

 

В соответствии с ГОСТ 8239-89,

(приложение №1, принимаем сечение балки стальной двутавровой № 33

Wх = 597 см³ ).

δ= М mах = 99∙10⁶ Н∙мм =165,8 МПа,

Wх 597∙10³Нм3

δ= δ mах -[δи] = 165,8 -160 ∙100= 3.6% <5%,

[δи] 160

что находится в разрешенных пределах (менее 5%).

 

Ответ: сечение балки - двутавр № 33.

 

Приложение №1:

 

 

Балки двутавровые (по гост 8239-89)

 

Обозначения: - h - высота балки; b - ширина балки; d - толщина стенки;

t - средняя толщина полки; А - площадь сечения; I - момент инерции;

W - момент сопротивления; i - радиус инерции; S - статический момент полусечения.

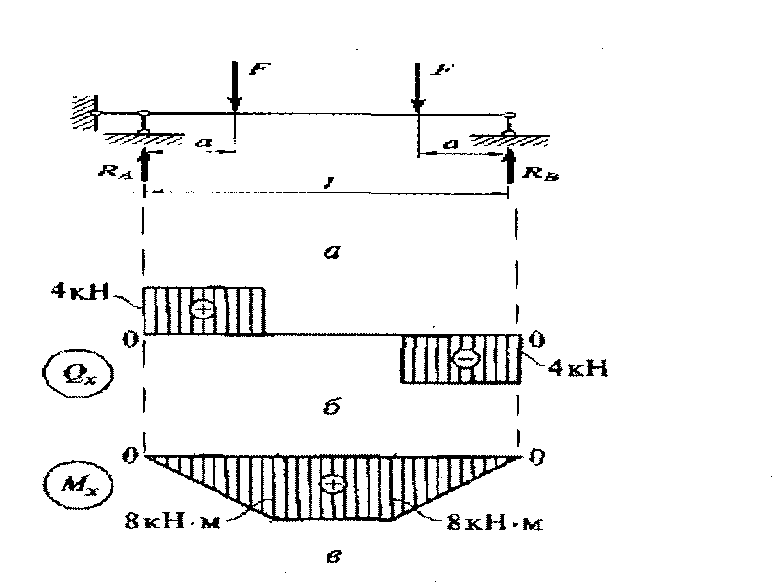
Пример решения задачи №2

Дано: Для двухопорной балки построить эпюры поперечных сил Q и изгибающих моментов М. Подобрать сечение стального двутавра, приняв [δи]=160 МПа.

F₁,=20 кН; F₂ = 30кН; М=10кН∙м; а = 4м; b = 4м; с = 2м;

 

 

а

 

б

 

в

 

Рисунок 1- Ход построения эпюр Q и M.

 

Решение:

1. Составляем уравнения равновесия плоской системы произвольно расположенных сил, из которых определяем опорные реакции балки:

 

∑М_А(F_R)= F₁ ∙ 4,0 -Vв∙8 – m+F₂∙10 =0, (1)

 

∑ Мв(F_R) = V_А∙8 - F₁∙4 - m + F₂∙2 =0, (2)

 

Из уравнения (2) находим Va:

V_в = (F₁∙4- m+F₂∙10) /8=(20∙4-10+30∙10)/8= 46.25кН,

 

Из уравнения (1) находим Vв:

V_А= (F₁∙4+ m -F₂ ∙2) /8=(20∙4+10-30∙2) /8=30/8= 3.75кН,

 

Проверяем правильность опорных реакций, составляя сумму проекций всех сил на ось Y:
∑F_RУ= V_А + Vв - F₁ - F₂ =3.75-20+46.25-30 50-50=0,
т.е. реакции определены верно.

 

2. Определяем значение поперечной силы - Q в характерных сечениях балки, которая обозначена цифрами 1,2,3,4 (рисунок-2а).

Q ₁= Q ₂^лев= V_А =3.75 кН,
Q ₂^прав= Q ₃^лев = V_А - F₁=3.75-20=-16.25 кН,

Q ₃^прав= Q ₃^лев ₊ V_в =-16.25+46.25= 30 кН,

Q ₄^лев ₌ Q ₃^прав=30 кН.

По найденным значениям строим эпюру поперечных сил - Q (рисунок-1б).

 

3. Аналогично определяем значения изгибающего момента - М в характерных сечениях балки:

М ₁=0;

М ₂ = V_А ∙4= 3.75∙4=15 кНм,
М ₃ ^лев= V_А∙8- F₁∙4=3.75∙8-20∙4= - 50 кНм,

М₃ ^прав= М ₃ ^лев – m=-50-10=- 60 кНм,

М₄ = 0

По найденным значениям строим эпюру изгибающих моментов -М (рисунок-. 1в).

 

4. По эпюре изгибающих моментов определяем положение опасного сечения балки (сечение, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае - это сечение 3, где

Мз=Мmах=60 кНм.

Из условия прочности балки на изгиб:

δ= М mах <[δи],

Wх

Wх = М mах=60∙10⁶Н∙мм = 0,375∙ 10⁶ мм ³ =375см³, [δи] 160 Н/мм²

В соответствии с ГОСТ 8239-89,

(приложение №1, принимаем сечение из стального двутавра № 27 Wх = 371 см³)

δ= М mах = 60∙10⁶ Н∙мм =161.7 МПа,

Wх 371∙10³Нм3

δ= δ mах -[δи] = 161,7 -160 ∙100= 0.01% <5%,

[δи] 160

что находится в разрешенных пределах (менее 5%).

 

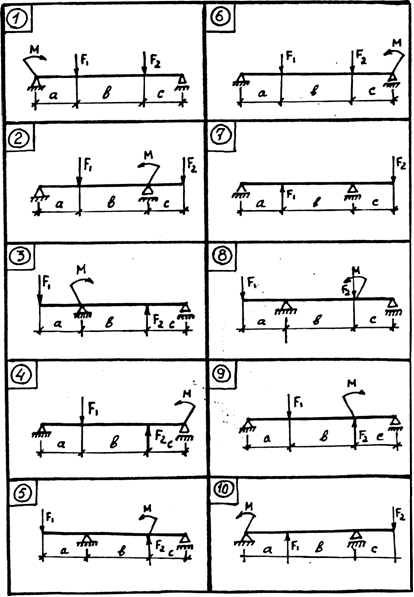
Ответ: V_в= 46.25кН, V_а= 3.75кН, сечение балки - двутавр № 27

Заданная схема № 1

 

 

Ответ:

 

Заданная схема № 2

 

 

 

Ответ

 

 

Заданная схема № 3

 

 

Ответ

 

 

 

 

Заданная схема № 4

 

 

Ответ

 

Заданная схема № 5

 

 

 

Ответ

 

Заданная схема № 6

 

 

Ответ

 

Приложение № 1