
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплект заданий текущей аттестацииСодержание книги
Поиск на нашем сайте
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ТЕКУЩЕЙ АТТЕСТАЦИИ ОП.07 ТЕХНИЧЕСКАЯ МЕХАНИКА специальность СПО: 22.02.06 Сварочное производство
Яровое 2018 РАЗРАБОТЧИКИ: КГБ ПОУ «Яровской политехнический техникум» преподаватель __ Т.А. Ролдухина
ОБЩИЕ ПОЛОЖЕНИЯ 1.1 Фонд контрольно-оценочных средств по ОП.07 Техническая механика 1.2. В результате аттестации по ОП осуществляется проверка следующих знаний и умений:
Литература Основные источники: 1. Техническая механика: учебник для студ. учреждений сред. проф. образования / А. А. Эрдеди, Н. А. Эрдеди. — М.: Издательский центр «Академия», 2014. — 528 с. Дополнительные источники: 1. Варданян Г.С., Андреев В. И., Атаров Н.М., Горшков А.А. Сопротивление материалов. Учебное пособие. М.: МГСУ. 2009-127с. 2. Андреев В. И., Паушкин А.Г., Леонтьев А.Н., Техническая механика. М.: Высшая школа, 2010-224с. 3. Атаров Н.М. Сопротивление материалов в примерах и задачах. М.: Инфра-М, 2010-262с. 4. Варданян Г.С., Андреев В. И., Атаров Н.М., Горшков А.А., Сопротивление материалов с основами теории упругости и пластичности. М.: Инфра-М, 2010-193с. 5. Лачуга Ю.Ф. Техническая механика. М.: КолосС, 2010-376с. 6. Ксендзов В.А. Техническая механика. М.: КолосПресс, 2010-291с. 7. Паушкин А.Г. Практикум по технической механике. М.: КолосС,2008-94с. 8. Интернет- ресурс «Техническая механика». Форма доступа: http://edu.vgasu.vrn.ru/SiteDirectory/UOP/DocLib13/Техническая%20механика.pdf 9. Интернет- ресурс «Техническая механика». Форма доступа: ru.wikipedia.org Практическая работа №1 Тема: Решение задач по теме «Статика твердого тела» Время выполнения работы – 2 часа Цель: освоить приемы решения задач по теме «Равновесие твердых тел» Порядок выполнения работы: 1. Изучить теоретический материал. 2. Решить задачи Примеры решения задач по теме «Равновесие твёрдых тел» При решении задач статики надо использовать условия равновесия (7.9). Причём от векторного уравнения для суммы сил следует перейти к проекциям сил на координатные оси. Иногда удобнее решать задачу, используя геометрическое правило сложения векторов. При равновесии многоугольник сил должен быть замкнутым, так как сумма сил равна нулю (подобный пример будет рассмотрен ниже). При записи для правила моментов сил надо подумать, как выбрать ось, чтобы плечи сил определялись наиболее просто и в сумме моментов сил содержалось меньше слагаемых. В задачах часто рассматриваются стержни, которые скрепляются шарнирно. При этом имеется в виду, что трение в шарнире отсутствует.
Р е ш е н и е. Силы натяжения тросов обозначим через
Оси координат выберем так, как показано на рисунке (7.5, в). При равновесии сумма проекций всех сил на оси координат равна нулю: T1x + T2х + mgх = 0, Т1у + Т2у + mgy = 0, или T1 - T1cos60° = 0, T1cos30° - mg = 0. Отсюда
Задача 2. Дверь люка АО, которая может поворачиваться в Р е ш е н и е. На дверь люка действуют три силы (рис. 7.6, б): сила тяжести m Выберем оси координат так, как показано на рисунке (7.6, б). Поскольку дверь находится в равновесии, то сумма моментов всех сил относительно, например, шарнира равна нулю: М1 + М + М2 = 0. Здесь M1, М, М2 — моменты сил Значит, М1 = -T l sinα, Теперь запишем правило моментов сил, учитывая знаки этих моментов: Отсюда находим силу натяжения верёвки:
Для нахождения силы реакции шарнира воспользуемся первым условием равновесия: m Запишем это векторное уравнение в проекциях на координатные оси: —Тх + Nx = 0, Ту + Ny - mg = 0, или Nх = Тcosα, Отсюда Nх = 86,5 H; Nхy = 150 H. Модуль силы N равен Угол, который образует сила
Задача 3. Лестница прислонена к стене. При каком минимальном угле наклона к полу она не будет падать? Коэффициенты трения между лестницей и стеной и между лестницей и полом соответственно равны μ1 и μ2.
Первое условие равновесия для лестницы имеет вид m Для записи правила моментов выберем ось вращения, проходящую через точку С, и запишем:
Из последнего уравнения следует: Выразим силы N1 и Fтp1 через силу тяжести. Для этого запишем уравнение (1) в проекциях на оси координат: на ось X: N1 - F.rp2 = О, По условию задачи требуется найти минимальное значение угла amin, поэтому берём максимальные значения сил трения, т. е. Fтp1 = μ1N1, и Fтp2 = μ2N2 Тогда Задачи для самостоятельного решения 1. Для запуска планера применяют резиновый канат. Определите силу, с которой планер действует на канат, в тот момент, когда две половины каната составляют между собой угол 90°, а каждая из них растянута силой 500 Н. 2. К концу рукоятки гаечного ключа длиной 20 см приложена сила 50 Н под углом 60° по отношению к рукоятке ключа. Определите момент этой силы. 3. Человек, открывая дверь, прикладывает силу 4 Н, которая направлена под углом 60° к плоскости двери в горизонтальном направлении. Момент силы равен 3,5 Н • м. Определите расстояние от ручки до оси вращения двери. 4. Труба массой 14 кг лежит на земле. Какую силу надо приложить к одному из концов трубы, чтобы его слегка приподнять? 5. На трапеции сидит гимнаст массой 60 кг. Он расположен на расстоянии 1/3 её длины, считая от одного из её концов. Определите натяжение тросов, на которых подвешена трапеция. Практическая работа №2 Практическая работа №3 Практическая работа №4 Пример решения задач Практическая работа №5 Задание Движение груза А задано уравнением y = at Цель работы – подставив заданные коэффициенты в общее уравнение движения, определить вид движения. Определить скорость и ускорение груза в моменты времени t Теоретическое обоснование Точки тела движутся по окружностям вокруг неподвижной оси (ось вращения). Закон равномерного вращательного движения: φ = φ Закон равнопеременного вращательного движения: φ = φ Закон неравномерного вращательного движения: φ = f(t Здесь φ – угол поворота тела за время t, рад; w – угловая скорость, рад/с; φ w ε - угловое ускорение, рад/с Угловая скорость: w = Угловое ускорение: ε = Кинематические графики вращательного движения представлены на рис. 3.1а, б.
А б Рис.3.1 Число оборотов вращения тела: z = φ(2π). Угловая скорость вращения: n, об/мин. w =
Параметры движения точки вращающегося тела (рис.3.2): v – линейная скорость точки В v = wr, м/с; (3.5) a a а а Порядок выполнения работы 1. Определить вид движения, подставив заданные коэффициенты в общее уравнение движения. 2. Определить уравнения скорости и ускорения груза. 3. Определить полное число оборотов шкива. 4. Определить нормальное и касательное ускорения точки на ободе шкива в указанные моменты времени. 5. Ответить на контрольные вопросы. Контрольные вопросы 1. В чем заключается принцип кинетостатики? 2. Могут ли при поступательном движении тела траектории его точек не прямыми линиями? 3. Равна ли скорость перемещения груза скоростям точек на ободе вращающегося шкива? 4. Как повлияет на скорость груза увеличение диаметра шкива при неизменной угловой скорости? 5. Какое ускорение (касательное или нормальное) характерно для точек вращающегося тела? Пример выполнения Для перемещения груза применена барабанная лебедка, привод которой состоит из электродвигателя 1 и редуктора 2 (понижает угловую скорость вала двигателя до требуемой на барабане). Барабан 3 служит для преобразования вращательного движения в поступательное движение груза. Диаметр барабана d = 0,2 м, а уравнение его вращения φ = 30t + 6t
1. Определяем кинематические характеристики движения барабана. Угол поворота барабана за время t Угловая скорость барабана w = Угловое ускорение барабана ε = 2. Кинематические характеристики движения любой точки на ободе барабана, например точки А, определяются через угловые характеристики движения барабана. Для момента времени t Скорость точки v 3. Кинематические характеристики груза равны соответствующим характеристикам любой точки тягового троса, а значит, и точки А, лежащей на ободе барабана. Литература: Таблица 3.1
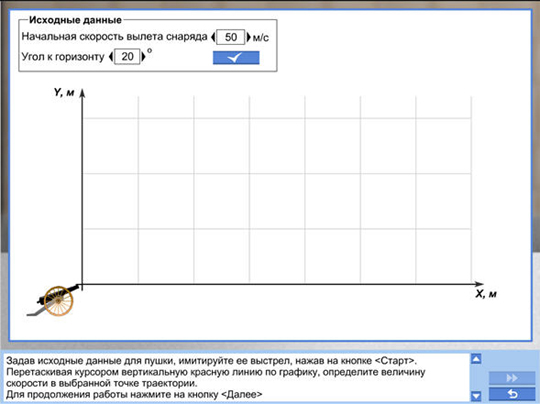
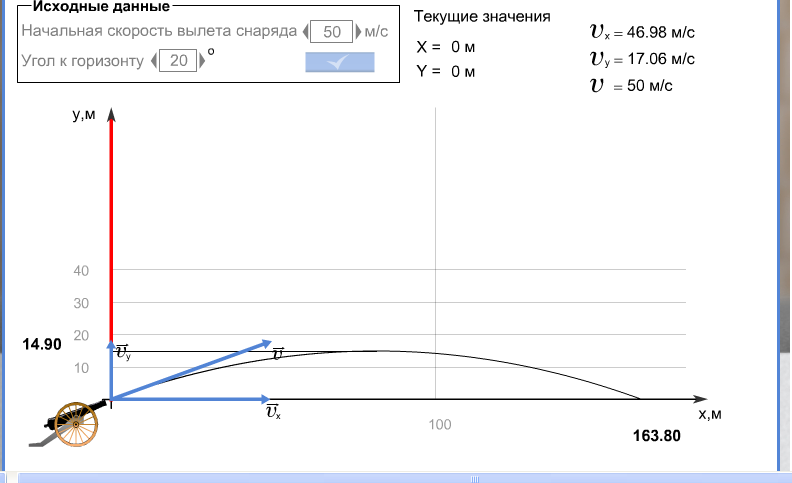
Цель работы: определить характеристики баллистической траектории движения тела, выявить от чего они зависят.
2. Рассчитайте максимальную высоту подъема и дальность полета снаряда по формулам.
Таблица 2
Рисунок 2
Рисунок 6
Рисунок 10 Практическая работа №6 Пример 1. Даны кривошипно-ползунный механизм, длины звеньев которого – кривошипа и шатуна – LOA и LAB соответственно, и угловая скорость кривошипа Определитьскорости и ускорения ползуна при различных положениях кривошипа. Решение. Выбираем масштабы длин Вычисляем длину отрезка Для построения графиков скоростей и ускорений (рис. 3.1) выбираются полюсные расстояния hu и ha, где hu – полюсное расстояние при построении графика скоростей, которое выбирается произвольной длины; рекомендуется его величину выбирать в пределах hu =30…40 мм; ha – полюсное расстояние при построении графика ускорений; его рекомендуется принимать в пределах ha =30…40 мм. Масштабы времени, скорости и ускорения вычисляют по формулам, вывод которых приводится ниже. Масштаб времени можно вычислить по формуле
где Т – период одного оборота кривошипа, с; LX – длина отрезка между точками 1 и 1 на графике (диаграмме) перемещений, мм. Так как период Т можно вычислить по формулам
где
Масштаб скорости можно вывести из условия, что скорость исследуемой точки является производной перемещения S по времени:
Здесь предполагается, что масштаб перемещений Так как
Масштаб ускорения, вывод которого аналогичен предыдущему, вычисляется по формуле
Для определения величины скорости или ускорения в каком-либо положении точки В необходимо длину ординаты соответствующего графика умножить на масштаб
Рис. 3.1. Совмещённые планы механизма, графики перемещений, скоростей и ускорений Рис.3.2
Модуль скорости точки Модуль скорости точки Модуль скорости точки
Видно, что модули скоростей точек Многоугольник План скоростей жёсткого звена – геометрическое место точек концов векторов абсолютных скоростей любых точек звена, если они построены из одной общей точки План скоростей всегда строится в масштабе. В дисциплине «Теория машин и механизмов» масштаб имеет размерность, поэтому его принято называть масштабным коэффициентом: План скоростей подобен самому звену, и повёрнут на девяносто градусов в сторону мгновенного вращения. Если план скоростей жёсткого звена подобен своему звену, то план скоростей механизма не подобен самому механизму, так как в отличие от жёсткого звена механизм есть изменяемая подвижная система. План скоростей механизма – совокупность планов скоростей отдельных звеньев, построенных из одной общей точки Пример 2. Дано: Требуется определить: Зададимся неким масштабным коэффициентом
Рис.3.3 Решение: Для построения плана скоростей механизма существуют различные методы, наиболее распространённым из которых является метод векторных уравнений, разработанный советскими учёными. Модуль скорости точки Допустим, что точка Вернём точку На плане скоростей векторы, исходящие из полюса скоростей
Рис.3.4 Модуль вектора нормального ускорения точки Модуль вектора тангенциального ускорения точки План ускорений механизма, как и план скоростей, не подобен самому механизму, и является совокупностью планов ускорений отдельных звеньев, построенных из одного полюса плана ускорений
Пример 3. Заданы геометрические параметры всех звеньев и угловая скорость Требуется определить ускорение точки
Рис.3.5
Решение: Построение плана скоростей. Скорости точек
Рис.3.6
Модул
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-12-25; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.107.11 (0.014 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

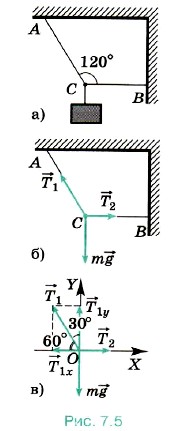 Задача 1. Груз висит на двух тросах (рис. 7.5, а). Угол АСВ равен 120°. Сила тяжести, действующая на груз, равна 600 Н. Определите силы натяжения тросов АС и СВ.
Задача 1. Груз висит на двух тросах (рис. 7.5, а). Угол АСВ равен 120°. Сила тяжести, действующая на груз, равна 600 Н. Определите силы натяжения тросов АС и СВ.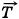 1 и
1 и 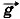 . Точка С находится в равновесии. Следовательно, сумма сил, действующих на неё, равна нулю:
. Точка С находится в равновесии. Следовательно, сумма сил, действующих на неё, равна нулю: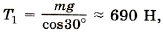 Т2 = T1cos60° ≈ 345 Н.
Т2 = T1cos60° ≈ 345 Н.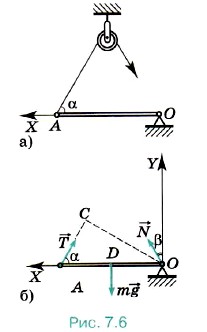 шарнире О без трения, удерживается в горизонтальном положении верёвкой (рис. 7.6, а). Определите натяжение верёвки и силу реакции шарнира, если верёвка образует с дверью угол α = 60°. Дверь однородна и на неё действует сила тяжести 300 Н.
шарнире О без трения, удерживается в горизонтальном положении верёвкой (рис. 7.6, а). Определите натяжение верёвки и силу реакции шарнира, если верёвка образует с дверью угол α = 60°. Дверь однородна и на неё действует сила тяжести 300 Н.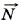 со стороны шарнира.
со стороны шарнира.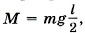 М2 = 0.
М2 = 0.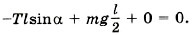

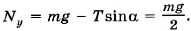

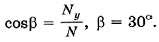
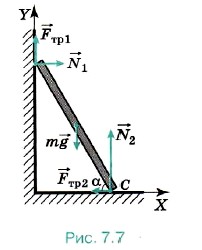 Р е ш е н и е. На лестницу действуют следующие силы (рис. 7.7): тяжести m
Р е ш е н и е. На лестницу действуют следующие силы (рис. 7.7): тяжести m 

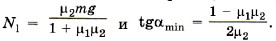
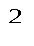 + bt + c, где [y] = м, [t] = c.
+ bt + c, где [y] = м, [t] = c. и t
и t  , а также скорость и ускорение точки В на ободе барабана лебедки (рис.3.3 и табл.3.1).
, а также скорость и ускорение точки В на ободе барабана лебедки (рис.3.3 и табл.3.1).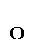 + wt. (3.1)
+ wt. (3.1)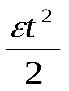 (3.2)
(3.2) ).
).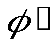 ; w = w
; w = w  .
.
 (3.4)
(3.4) Рис.3.2
Рис.3.2 - касательное ускорение точки В
- касательное ускорение точки В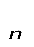 - нормальное ускорение точки В
- нормальное ускорение точки В

 Рис. 3.3
Рис. 3.3








 .
. , м/мм, где AO – длина отрезка, мм, изображающая кривошип длиной LОА на строящемся плане механизма; эта длина выбирается произвольно с учётом того, что совмещённые планы механизма должны разместиться на отведённом месте чертежа, а сам масштаб длин был бы удобен для дальнейших расчётов.
, м/мм, где AO – длина отрезка, мм, изображающая кривошип длиной LОА на строящемся плане механизма; эта длина выбирается произвольно с учётом того, что совмещённые планы механизма должны разместиться на отведённом месте чертежа, а сам масштаб длин был бы удобен для дальнейших расчётов. , мм, изображающего шатун на плане механизма. При построении совмещенных планов механизма используют метод засечек (рис. 3.1).
, мм, изображающего шатун на плане механизма. При построении совмещенных планов механизма используют метод засечек (рис. 3.1).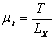 ,
, , или
, или  , с,
, с, – угловая скорость кривошипа, 1/с; n1 – частота вращения кривошипа, об/мин, то масштаб времени
– угловая скорость кривошипа, 1/с; n1 – частота вращения кривошипа, об/мин, то масштаб времени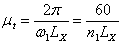 , с/мм.
, с/мм.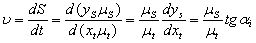 .
. и масштаб времени
и масштаб времени  являются постоянными величинами.
являются постоянными величинами. , то
, то  , отсюда
, отсюда ,
,  .
. ,
,  .
.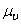 или
или 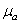 соответственно.
соответственно.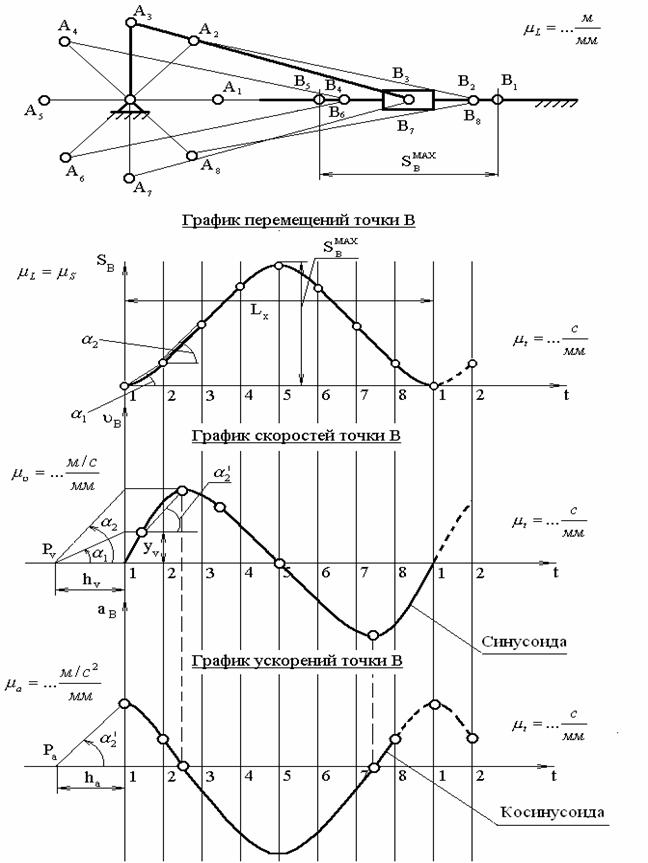
 можно определить по формуле:
можно определить по формуле:  , а линия действия этого вектора будет перпендикулярная отрезку
, а линия действия этого вектора будет перпендикулярная отрезку  .
. можно определить по формуле:
можно определить по формуле:  , а линия действия этого вектора будет перпендикулярная отрезку
, а линия действия этого вектора будет перпендикулярная отрезку  .
.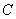 можно определить по формуле:
можно определить по формуле:  , а линия действия этого вектора будет перпендикулярная отрезку
, а линия действия этого вектора будет перпендикулярная отрезку  .
.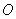 - мгновенный центр вращения.
- мгновенный центр вращения.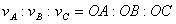 .
. подобен многоугольнику
подобен многоугольнику  , так как он образован взаимно перпендикулярными и пропорциональными прямыми. Поэтому рис.3.2 представляет собой план скоростей треугольника
, так как он образован взаимно перпендикулярными и пропорциональными прямыми. Поэтому рис.3.2 представляет собой план скоростей треугольника  , то есть треугольник
, то есть треугольник  является планом скоростей треугольника
является планом скоростей треугольника  , называемой полюсом плана скоростей.
, называемой полюсом плана скоростей. ,
,  .
. ,
,  и
и  (рис.3.3).
(рис.3.3). .
.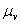 .
.
 . Линия действия вектора скорости точки
. Линия действия вектора скорости точки  , а сам вектор направлен в сторону вращения звена
, а сам вектор направлен в сторону вращения звена  совершают переносное движение со скоростью
совершают переносное движение со скоростью  , то есть
, то есть  . С одной стороны
. С одной стороны  , с другой стороны
, с другой стороны  .
. на действительную траекторию
на действительную траекторию  , для чего придадим точке
, для чего придадим точке  со скоростью относительного движения
со скоростью относительного движения  .
. является планом скоростей звена
является планом скоростей звена  является планом скоростей звена
является планом скоростей звена  . Линия действия этого вектора будет перпендикулярна звену
. Линия действия этого вектора будет перпендикулярна звену  . Линия действия этого вектора будет параллельна звену
. Линия действия этого вектора будет параллельна звену  .
. .
.
 равны нулю, поэтому на плане скоростей точки
равны нулю, поэтому на плане скоростей точки  и
и  совпадают с полюсом плана скоростей
совпадают с полюсом плана скоростей 



