Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Построение эпюр продольных сил и нормальных напряжений
Время выполнения работы – 2 часа Цель: Двухступенчатый стальной брус, длина ступеней которого указана на схеме, нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв Задача: Числовые значения сил F1 и F2, а так же площадей поперечных сечений ступеней А1 и А2 взять из таблицы.
Теоретическое обоснование Виды нагружения бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор – N = ∑F Величина продольных сил в разных сечениях бруса неодинакова. График, показывающий изменение величины продольных сил в сечении бруса по его длине, называется эпюрой продольных сил. Закон распределения напряжений может быть определен из эксперимента. Установлено, что если на стержень нанести прямоугольную сетку, то после приложения продольной нагрузки вид сетки не изменится, она по-прежнему останется прямоугольной, а все линии прямыми. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций, а на основании закона Гука (σ = Eε) и нормальных напряжений S = const. Тогда N = S· F, откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении
σ A – площадь около рассматриваемого участка бруса; N– равнодействующая внутренних сил в пределах этой площадки (согласно метода сечений). Для обеспечения прочности стержня должно выполняться условие прочности - конструкция будет прочной, если максимальное напряжение ни в одной точке нагруженной конструкции не превышает допускаемой величины, определяемой свойствами данного материала и условиями работы конструкции, то есть σ ≤ [σ ], τ ≤ [τ] (5.3) При деформации бруса меняется его длина на Поэтому рассматривают Экспериментально показано, что В пределах упругой деформации выполняется закон Гука: Порядок выполнения работы 1. Разбиваем брус на участки, ограниченные точками приложения сил (нумерацию участков ведем от незакрепленного конца); 2. Используя метод сечений, определяем величину продольных сил в сечении каждого участка: N = ∑F 3. Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением бруса (или рядом) проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответствующие в выбранном масштабе продольным силам (положительное значение откладываем вверх (или вправо), отрицательное – вниз (или влево). 4. Определяем общее перемещение бруса и строим эпюру перемещений δ 5. Ответить на контрольные вопросы. Контрольные вопросы 1. Что называется стержнем? 2. Какой вид нагружения стержня называются осевым растяжением (сжатием)? 3. Как вычисляется значение продольной силы в произвольном поперечном сечении стержня? 4. Что такое эпюра продольных сил и как она строится? 5. Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня, и по какой формуле они определяются?
6. Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций? 7. Что называется модулем упругости Е? Как влияет величина Е на деформации стержня? 8. Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня. 9. Что происходит с поперечными размерами стержня при его растяжении (сжатии)? 10. Что такое коэффициент Пуассона? В каких пределах он изменяется? 11. С какой целью проводятся механические испытания материалов? Какие напряжения являются опасными для пластичных и хрупких материалов? Пример выполнения Построить эпюры продольных сил и нормальных напряжений для нагруженного стального бруса (рис. 5.1). Определить удлинение (укорочение) бруса, если E
Рис.5.1 Дано: F l Решение. Определяем продольные силы и строим их эпюру: N N N N Определяем величину нормальных напряжений и строим их эпюру:
Используя видоизмененный закон Гука, определяем удлинение бруса:
Практическая работа №8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-12-25; просмотров: 1167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.174.239 (0.019 с.) |
 МПа.
МПа.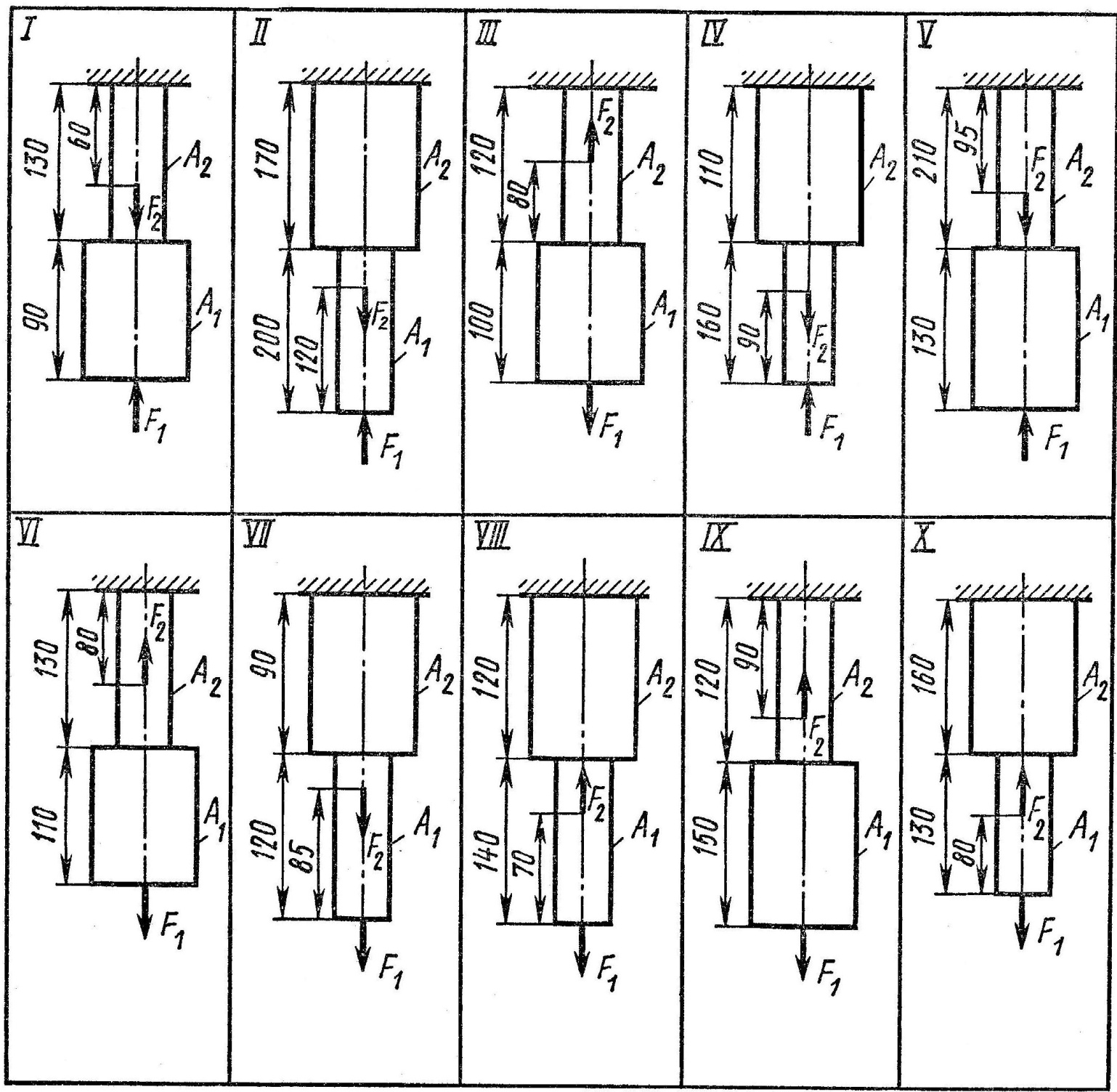
 , называемый растяжением или сжатием. Равнодействующая внешних сил прикладывается в центре тяжести поперечного сечения и действует вдоль продольной оси. Внутренние силы определяются с помощью метода сечений. Нормальная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения
, называемый растяжением или сжатием. Равнодействующая внешних сил прикладывается в центре тяжести поперечного сечения и действует вдоль продольной оси. Внутренние силы определяются с помощью метода сечений. Нормальная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения (5.1).
(5.1).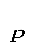 =
=  МПа (5.2)
МПа (5.2) и поперечный размер – на
и поперечный размер – на  . Эти величины зависят и от начальных размеров бруса.
. Эти величины зависят и от начальных размеров бруса. – продольная деформация; (5.4)
– продольная деформация; (5.4)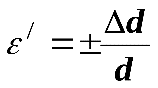 – поперечная деформация. (5.5)
– поперечная деформация. (5.5) , где μ = 0, …, 0,5 – коэффициент Пуассона. Примеры: μ=0 – пробка, μ=0,5 – резина,
, где μ = 0, …, 0,5 – коэффициент Пуассона. Примеры: μ=0 – пробка, μ=0,5 – резина,  – сталь.
– сталь. , где E – модуль упругости, или модуль Юнга.
, где E – модуль упругости, или модуль Юнга. поперечных сечений.
поперечных сечений.

 = 2 kH, F
= 2 kH, F  = 5 kH, F
= 5 kH, F  = 2 kH, A
= 2 kH, A  , А
, А 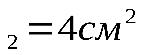 , l
, l  = 150 мм.
= 150 мм. = - F
= - F