
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение положений звеньев механизма
Взаимное расположение звеньев движущегося механизма все время меняется, но в каждый данный момент времени расположение звеньев является вполне определенным. Графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени, называется планом механизма. Ряд последовательных планов механизма, построенных для моментов времени, следующих друг за другом, называется планом положений и позволяет наглядно проследить за движением механизма. Построение плана положений механизма начинают с изображения того звена, положение которого задано для данного момента времени. Кривошипно-ползунный механизм
Рис.1 Из центра О - оси вращения кривошипа ОА радиусами
Практическая работа №14 Тема: Построение плана скоростей Практическая работа №15 Тема: Построение плана ускорений Время выполнения работы – 4 часа Цель: 1. Знакомство с методами кинематического исследования плоского механизма. 2. Приобретение навыков для решения задач кинематического исследования методом планов.
Определение скоростей и ускорений методом планов Скорости и ускорения звеньев также можно определять методом планов. Планом скоростей (ускорений) механизма называется чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям (ускорениям) различных точек звеньев механизма в данный момент. Векторы абсолютных скоростей (ускорений) на плане откладываются от одной точки - полюса, обозначаемого на плане скоростей буквой р, на плане ускорений буквой р, а отрезки, соединяющие концы векторов, определяют относительные скорости (ускорения) соответствующих точек звеньев в данный момент.
Построение планов скоростей и ускорений базируется на определениях движения (абсолютное, относительное, переносное) и теоремах о сложении векторов скоростей и ускорений, рассматриваемых в разделах теоретической механики. Напомним эти определения и теоремы: Движение точки или тела по отношению к основной (неподвижной) системе отсчета называется абсолютным движением. Движение точки или тела по отношению к подвижной системе отсчета называется относительным движением. Движение подвижной системы отсчета по отношению к основной системе отсчета называется переносным движением. Теорема сложения скоростей при сложном движении точки гласит: абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей этой точки: ++ (1) При определении переносной скорости точки предполагается, что относительное движение точки остановлено. При плоском движении звена переносное движение является поступательным со скоростью произвольно выбранной точки звена, принятой за полюс, а относительное движение является вращательным вокруг этой точки. Абсолютное ускорение любой точки звена при плоскопараллельном (плоском) движении твердого тела равно геометрической сумме двух ускорений: ускорения в поступательном переносном движении и ускорения во вращательном относительном движении: = + = + + (2) где - и - соответственно нормальное ускорение в относительном движении, направленное по радиусу вращения точки к центру кривизны траектории, и касательное ускорение, направленное перпендикулярно радиусу вращения. В случае, когда переносное движение при сложном движении точки не является поступательным, абсолютное ускорение точки равно векторной сумме трех ускорений: переносного, относительного и кориолисова:
, где - вектор относительной скорости точки определяется из соотношения:
Для удобства вводим в качестве подстрочного индекса обозначение точки и звена, например: и т.д.
Например, векторное уравнение обозначает: абсолютная скорость равна геометрической сумме переносной скорости, определяемой движением точки В, и относительной скорости точки С при вращении звена СВ вокруг точки В. Это векторное уравнение решается, если оно содержит не более двух неизвестных. Если известны траектории бб и вв описываемые точками С и В в абсолютном движении (рис.З, а), то направление всех скоростей в этом уравнении определено по касательной к траектории движения. Необходимо знать модуль скорости только одной из точек (например, ||). Решение приведенного векторного уравнения показано на рис.3,б в виде отрезков, пропорциональных соответствующим скоростям:
,
где. Скорость любой точки S на звене ВС находим по известной из теоретической механики теоремы подобия отрезков на схеме звена и плане скоростей: отрезки прямых линий, соединяющие точки на схеме звена механизма, и отрезки прямых линий, соединяющие концы секторов относительных скоростей этих точек на плане скоростей, образуют подобные, сходственно расположенные фигуры (рис. 3, б). bs = cb (BS / CB) Для определения ускорения точки С запишем уравнение (2) в следующем виде:
,
Нормальные ускорения определяются по формулам:
|
||||||
|
Последнее изменение этой страницы: 2019-12-25; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.232 (0.01 с.) |
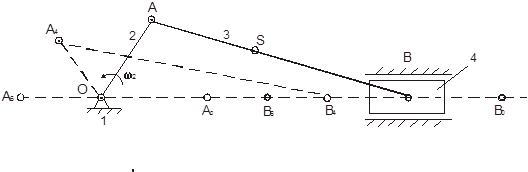
 и
и  на оси X - Xдвижения ползуна отмечаем В0 - правое В6 - левое крайние ползуна В. Прямые ОА0 В0 и ОА6 В6 - положения механизма, соответствующие крайним положениям В0 и В6 ползуна. Траекторию пальца А кривошипа от точки А0 делим на 12 равных частей и из полученных точек А1, А2, А3 … А11 радиусами АВ=
на оси X - Xдвижения ползуна отмечаем В0 - правое В6 - левое крайние ползуна В. Прямые ОА0 В0 и ОА6 В6 - положения механизма, соответствующие крайним положениям В0 и В6 ползуна. Траекторию пальца А кривошипа от точки А0 делим на 12 равных частей и из полученных точек А1, А2, А3 … А11 радиусами АВ= 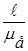 =… отмечаем положения В1, В2, В3 …В11 ползуна на линии В0 В6. Соединив точки А1, А2, А3 … А11 с центром О и соответствующими точками В1, В2, В3 …В11, получим планы механизма. Кривая, последовательно соединяющая центры S0, S1, S2 …S11 шатуна в различных его положениях, будет шатунной кривой.
=… отмечаем положения В1, В2, В3 …В11 ползуна на линии В0 В6. Соединив точки А1, А2, А3 … А11 с центром О и соответствующими точками В1, В2, В3 …В11, получим планы механизма. Кривая, последовательно соединяющая центры S0, S1, S2 …S11 шатуна в различных его положениях, будет шатунной кривой.











