Где - радиусы кривизны соответствующих траекторий абсолютного и относительного движения.

Касательное ускорение а_В' также задано (если щ=const, то а_В' =0). В этих двух уравнениях лишь два неизвестных, которые можно найти построением плана ускорений, используя правило сложения векторов.

Решение векторных уравнений приведено на рис. 3, в.

;

Рис. 3 а)

в)

б)

Рис. 3

Отрезки,, соответствуют нормальным ускорениям в масштабе. Отрезки п_сс, п_Bb, п_CBс пропорциональны тангенциальным ускорениям, причем отрезки п_Bb=а_B^t/м_a, вычисляем предварительно, а отрезки пс_СB и п_сc позволяют определить искомые ускорения

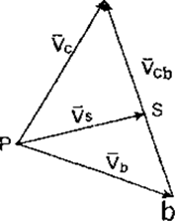
Ускорение любой другой точки на звене ВС, например точки S (рис.З, а), находят, используя теорему подобия: Отрезки прямых линий, соединяющие точки на схеме звена механизма, и отрезки прямых линий, соединяющие концы векторов относительных скоростей и ускорений этих точек на плане скоростей, образуют подобные, сходственно расположенные фигуры (рис.3, в).

bs = bc BS / BC и a_s = р s

При кинематическом исследовании механизма расчет и построение планов скоростей и ускорений начинаем от ведущего звена и затем производим расчет и построение по группам Ассура в порядке их присоединения.

Построение плана скоростей

Построение плана скоростей рассмотрим на примере плоского шестизвенного механизма второго порядка (рис.4, а). Угловую скорость принимаем постоянной: W₁ = const. Необходимо определить абсолютные скорости точек В, С, D, F и относительные скорости звеньев V_BC,V_CE, V_DF.

Определяем величину и направление скорости точки В. Так как ведущее звено 1 вращается с постоянной угловой скоростью, то линейная скорость точки В постоянна по модулю и равна

V_B=W₁L_AB,

где L_AB -длина звена АВ. Вектор скорости V_B направлен по касательной к траектории движении, т.е. перпендикулярно АВ, в сторону вращения кривошипа АВ.

Выбрав полюс р и величину отрезка pb, изображающего вектор V_B (рис.4),

определяем масштабный коэффициент плана скоростей

Откладываем отрезок рb абсолютной скорости точки В из полюса р перпендикулярно отрезку АВ. Обозначаем конец вектора стрелкой или буквой b.

2. Определяем скорости двухповодковой группы Ассура 2-3. Для каждой двухповодкой группы можно составить два векторных уравнения, связывающих скорость одной выбранной точки со скоростями двух других точек. В нашем примере известны скорости точек В и Е, к которым присоединена кинематическая группа ВСЕ. Следовательно, целесообразно рассмотреть связи точки С с точками В и Е.

По теореме о плоском движении связи между скоростями указанных точек могут быть представлены векторными уравнениями:

Векторы относительных скоростей и направлены по касательным к траекториям относительного движения, т.е. перпендикулярна СВ; перпендикулярна СЕ. Так как =0, то абсолютная скорость равна относительной скорости звена Поэтому в двух написанных уравнениях имеется лишь два неизвестных элемента - модули векторов и, которые могут быть определены построением плана скоростей.

Через точку b - конец найденного ранее отрезка pb плана скоростей (рис.4, б) - проводим линию, перпендикулярную направлению ВС, а из точки е, совпадающей с полюсом р, проводим линию, перпендикулярную СЕ. Пересечение указанных лучей обозначаем точкой с. Отрезок рс изображает абсолютную скорость точки C, отрезок bс - относительную скорость звена V_CB. Величины этих скоростей находим по формулам:

Угловые скорости звеньев 2 и 3 определяем из выражений:

и

Направления угловых скоростей W₂ и W₃ могут быть определены следующим образом. Мысленно прикладывая векторы к точке С, видим, что вращение звеньев 2 и 3 происходит в направлении, обратном вращению часовой стрелки.

3. Для нахождения скорости точки D коромысла можно воспользоваться теоремой подобия для скоростей: Отрезки прямых линий, соединяющие точки на схеме звена механизма, и отрезки прямых пиний, соединяющие концы векторов относительных скоростей этих точек на плане скоростей, образуют подобные, сходственно расположенные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90 градусов.

Согласно теореме подобия, отрезок cd на плане скоростей подобен отрезку коромысла CD (рис.5,а), следовательно, положение точки D на векторе относительной скорости cd определим из отношения отрезков cd/ce=CD/CE.

Соединяя найденную точку d (рис.4,б) с полюсом р плана скоростей, находим направление вектора pd скорости; модуль вектора определяется формулой:

4. Определим скорости двухповодковой группы Ассура 4-5. Связь между скоростями точек D, F, G устанавливается векторными уравнениями:

,

где - скорость точки F при вращении звена FD относительно точки D, направленная по касательной к траектории относительно движения, т.е., перпендикулярна FD, - скорость точки F относительно стойки, направленная вдоль линии ОХ.

Через точку d проводим линию перпендикулярно направлению FD, а через полюс р - линию, параллельную ОХ. Пересечение указанных лучей обозначаем точкой f. Отрезок pf изображает абсолютную скорость точки f, а отрезок df -относительную скорость звена DF (рис.4, б).

Величины этих скоростей находим по формулам:

;

Угловую скорость звена DF находим из уравнения W₄=V_DF / L_DF.

масштаб ведущий механизм абсолютное ускорение теорема подобия

· а)

· б)

· в)

г)

Рис. 4

Построение плана ускорений

Построение плана ускорений рассмотрим на примере того же положения механизма, для которого рассмотрено построение плана скоростей. Необходимо определить: абсолютные ускорения точек В, С, D, F и относительные ускорения звеньев СВ, СЕ, FD.

1. Определим величину и направление ускорения точки В:

Ускорение точки В при равномерном вращении ведущего звена равно нормальному ускорению:

a_B = a_BDⁿ Ч W_l Ч L_AB

Вектор нормального ускорения направлен вдоль прямой ВА от точки В к центру А. Выбрав полюс р и величину отрезка рb, изображающего вектор а_B (рис. 2, б), определяем масштабный коэффициент плана ускорений

м_a=а_B / рb

Откладываем отрезок рb ускорения точки В из полюса р параллельно направлению. Обозначаем конец вектора стрелкой и буквой b.

2) Определяем ускорения двухповодковой группы Ассура 2 - 3. Для этой группы Ассура можно составить два векторных уравнения, связывающих ускорения точки С с ускорениями точек В и Е, которые известны:

Величины в берем из плана скоростей. Нормальные составляющие ускорения всегда направлены к центру вращения. Тангенциальные составляющие уравнения всегда перпендикулярны нормальному. Так как а_E=0, то в двух написанных уравнениях имеется лишь два неизвестных элемента - модули векторов и, которые могут быть определены построением плана ускорений.

Через точку b (рис.4, в) ранее построенного отрезка рb плана ускорений проводим линию, параллельную ВС (рис.4, а), и откладываем на ней отрезок

,

направленный от точки С к центру В. Этот отрезок пропорционален нормальному ускорению с учетом выбранного масштаба.

Из точки е, совпадающей с полюсом р (рис.4 в), проводим линию, параллельную СЕ, и откладываем на ней отрезок

направленный от точки С к центру Е (рис.4, а). Отрезок пропорционален ускорению а_CEⁿ с учетом масштаба. Затем через точки п_СB и п_CE (рис.4,в) проводим лучи, перпендикулярные прямым ВС и СЕ. Точка с их пересечения будет искомой. Отрезок рc изображает полное ускорение а_с, модуль которого равен. Отрезки сп_CB и сп_CE изображают ускорения а_CB^t и a_CE^t,модуль которых соответственно равен, а отрезок cb - полное относительное ускорение а_{CB ,} модуль которого равен.

Угловые ускорения звеньев 2 и 3определяем по формулам

Направление их находим, мысленно перенося ускорение и в точку С (рис.4, а) и рассматривая движение точки С относительно В и Е. Угловые ускорения е₂ и е₃ направлены против часовой стрелки.

Согласно теореме подобия, отрезок cd на плане ускорений подобен отрезку CD на кинематической схеме механизма, следовательно, положение точки d на векторе относительного ускорения определится из соотношения отрезков cd / ce= CD / CE.

Соединяя найденную точку d с полюсом р плана ускорений, находим направление вектора рd. Модуль вектора определяется по формуле

a_D= рd Ч м_{a .}

3. Определяем ускорения группы Ассура 4 - 5. Связи между ускорениями точек D, F, G устанавливаются векторными уравнениями:

берем из плана скоростей;

=0, так как звено G (стойка) - неподвижно;

=0 - кориолисово ускорение точки G=0;

- относительное ускорение точки F (направлено вдоль линии ОХ).

В двух написанных уравнениях имеются лишь два неизвестных элемента - модули и, которые могут быть определены построением плана ускорений.

Через точку d - конец ранее найденного отрезка рd (рис.З, в) - проводим линию параллельно FD и откладываем на ней отрезок п_FD, направленный от точки F к центру D. Через точку п_FD^t проводим перпендикулярную линию, так как вектор тангенциального ускорения a_FD^t всегда перпендикулярен нормальному.

Переходим к построению решения второго векторного уравнения. Для этого через полюс плана я-проводим линию ускорения a_FDⁿ, параллельную направлению движения ползуна F. Точка пересечения этой линии с перпендикуляром, проведенным через точку n_FD, дает точку f. Соединяя найденную точку f с полюсом р плана ускорений, находим направление вектора рf. Модуль вектора определяем по формуле

a_F=.

Угловое ускорение звена 4 находим по формуле(рис.4, а, в)

Пример 3

Проведем кинематический анализ кривошипно-ползунного механизма компрессора. Его схема показана на рис.5, а.

Рис. 5 Кинематический анализ кривошипно-ползунного механизма компрессора: а) схема, б) план положения, в) план скоростей, г) план ускорений

Напомним, что для проведения кинематического анализа необходимо знать количество звеньев, кинематических пар, групп Асура и т.д. Поэтому исследование механизма целесообразно начинать со структурного анализа.

Построим планы скоростей и ускорений кривошипно-ползунного механизма компрессора (рис. 5, а). Найдем скорость и ускорение точек C,D, угловую скорость и угловое ускорение шатуна ВС.

Дано: ц_l = 45°, L_AB= 0,05м, L_BC = 0,20м, L_BD = 0,10м, угловая скорость кривошипа АВ постоянна и равна щ₁= 80 сек^-1.

Решение

1) Проводим структурный анализ и устанавливаем класс заданного механизма. Число звеньев к = 4, число подвижных звеньев n = 3, число кинематических пар V класса р₅ = 4, степень подвижности механизма равна

щ = Зп - 2р₅ = 3 Ч 3 - 2 Ч 4 = 1

Механизм образован присоединением к ведущему звену АB и стойке 4 группы второго класса второго вида, состоящей из звеньев 2 и 3.

2) Строим план положения механизма (рис. 5, б ). Задаемся длиной отрезка А В = 25 мм, вычисляем масштаб схемы механизма:

,

по нему находим длины отрезков ВС и BD:

По полученным размерам и заданному углу ц_l, строим план положения механизма (рис. 5, б)

3) Строим план скоростей для группы 2,3. Построение ведем по следующим двум векторным уравнениям:

,

где - скорость точки В, по модулю равная

V_B = щ_l l_AB = 80 Ч 0,05 = 4 мсек^-1

и направленная перпендикулярно линии АВ в сторону, соответствующую направлению угловой скорости звена АВ; - скорость точки С при вращении звена ВС вокруг оси шарнира В, по модулю равная

V_CB = щ₂ l_BC

(- угловая скорость звена ВС, которая пока нам неизвестна) и направленная перпендикулярно линии ВС;

- скорость точки С₄ стойки 4, совпадающей с точкой С (она равна нулю, так как звено 4 неподвижно);

- относительная скорость точки С в ее движении относительно точки С₄ (ее модуль неизвестен, а направлена она вдоль линии Ах).

Построение плана скоростей ведем в такой последовательности (рис.5, в). Строим решение первого векторного уравнения, указанного выше: от полюса р откладываем отрезок (pb), изображающий скорость точки В, перпендикулярно линии АВ и в соответствии с направлением вращения звена АВ, причем длину отрезка (pb) выбираем равной (АВ) = 25 мм, т. е. строим план в масштабе кривошипа; из точки b проводим направление скорости V_CB - линию, перпендикулярную ВС. Переходим к построению решения второго векторного уравнения, указанного выше: из точки р надо было бы отложить скорость, но она равна нулю, поэтому точку С₄ совмещаем с точкой р; из точки С4 или, что тоже, из точки р проводим направление скорости - линию, параллельную Ах, до пересечения с линией, проведенной перпендикулярно ВС, и получаем точку с - конец вектора скорости точи С. Помещаем в полюс плана точку а и на этом заканчиваем построение плана скоростей для всего механизма. Скорость точки D находим по правилу подобия: вектор этой скорости должен делить отрезок (bc) в том же отношении, в каком точка D делит отрезок ВС, т.е.

Вычисляем масштаб плана скоростей:

Скорость V_C точки С равна

Угловая скорость щ₂ звена ВС равна

На рис.5, б построен повернутый план скоростей непосредственно на схеме механизма. В этом плане полюс р совмещен с точкой А. Направление вектора скорости точки В совпадает с направлением АВ, направление скорости V_CB является продолжением линии ВС, а направление скорости точки С перпендикулярно линии А.

Строим план ускорений для группы 2,3. Этот план строится по таким двум векторным уравнениям:

и направленное параллельно линии АВ от точки В к точке А; - нормальное ускорение точки С во вращательном движении звена ВС относительно точки В, по модулю равное и направленное параллельно линии ВС от точки С к точке В.

- касательное ускорение точки С в том же движении звена ВС, по модулю равное

a_CB^l = е² l_BC ,

где е₂ - угловое ускорение звена ВС, пока нам неизвестное и направленное перпендикулярно линии ВС;

- ускорение точки С₄ (точка звена 4; оно равно нулю, так как звено 4 неподвижно);

- кориолисово ускорение точки С в движении ее относительно точки С₄, равное нулю, потому что звено 4 неподвижно;

- относительное (релятивное) ускорение точки С в ее движении относительно точки С₄, оно направлено вдоль линии Ах.

Построение плана ускорений ведем в такой последовательности (рис.5, г). Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана р откладываем отрезок (рb), изображающий ускорение a_В, параллельно линии АВ. Длину (рb) выбираем равной (АВ)=25 мм, т.е. строим план в масштабе кривошипа, при этом масштабы планов ускорений соответственно будут равны

От точки b откладываем отрезок (bn_cn), изображающий ускорение. Длина отреза (bn_cn) вычисляется так:

Через точку n_CB проводим направление ускорения - линию, перпендикулярную линии ВС.

Переходим к построению решения второго векторного уравнения, указанного выше. Для этого от полюса плана р откладываем вектор ускорения, но так как модуль его равен нулю, точка С₄ совпадает с точкой р. С этой же точкой совпадает конец вектора ускорения - точка k (ускорение равно нулю). Из точки k или, что то же, из точки р проводим направление ускорения - линию, параллельную Ах. Точка пересечения ее с линией, проведенной перпендикулярно ВС, дает точку с - конец вектора ускорения точки С. Соединяем точки с и b и получаем вектор полного ускорения С при вращении звена ВС относительно точки В, т.е. а_СВ. В точку р помещаем точку а. На этом заканчиваем построение плана ускорений механизма. Конец вектора ускорения точки D находим по правилу подобия:

Соединив точку d с полюсом плана р, получаем отрезок (рd), изображающий ускорение точки D. Величину ускорения точки С находим так:

а величина углового ускорения звена ВС

Таким образом, мы подробно рассмотрели задачи о построении скоростей и ускорений групп II класса первого и второго видов. Составление уравнений и построение планов скоростей и ускорений групп II класса других видов выполняется аналогично.

Порядок выполнения работ

1. Ознакомиться с выданной преподавателем кинематической схемой механизма.

Проверить наличие данных для решения задачи.

· 2. Вычертить кинематическую схему механизма с учетом выбранного масштаба.

· 3. Определить перемещение звеньев и траекторий, описываемых точками звеньев.

· 4. Построить план скоростей.

· 5. Построить план ускорений.

В отчете представить:

· 1) цель работы;

· 2) кинематическую схему;

· 3) построенный план механизма;

· 4) построенный план скоростей;

· 5) построенный план ускорений.

Контрольные вопросы:

· - Какие задачи решает кинематическое исследование механизма?

· - Какими способами производится кинематическое исследование механизма?

· - Что следует понимать под масштабом?

· - Для чего необходимо определение перемещения звеньев и траекторий, описываемых точками звеньев?

· - Что называется планом скоростей?

· - Что называется планом ускорений?

Контрольное задание:

Провести кинематическое исследование механизмов, приведенных в приложении.

Исходные расчетные данные

структурный кинематический схема механизм

Параметры ползуна: геометрические размеры: масса кривошипа:

F_p =1.8 kH l_O1A=120 мм lO2B = 364.4 m=1.2 кг

n=120об/мин b=173.2 мм

h=140 мм (Ход) a=600 мм

Практическая работа №16