Классификация кинематических пар и цепей

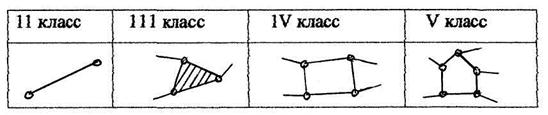
Кинематические пары могут быть:

 поступательными и вращательными,

 низшими и высшими,

 одноподвижными и многоподвижными (I….V класса).

Поступательными называется пары, допускающие только поступательное движение звеньев, вращательными – пары, допускающие только вращательное движение вокруг некоторой оси.

К низшим парам относятся пары, у которых звенья касаются между собой по всей поверхности. К ним относятся поступательные и вращательные кинематические пары.

К высшим относятся пары, звенья которых соприкасаются друг другом в точке или по линии. К ним относятся фрикционные, кулачковые зубчатые, храповые и мальтийские пары.

В зависимости от числа условий связи, все кинематические пары делятся на классы. Они могут быть:

- пятиподвижными (сферич.), S=1, I класс,

- четырехподвижными (цилиндр), S=2, II класс,

- трехподвижными (сферич.), S=3, III класс,

- двухподвижными (цилиндр), S=4, IV класс,

- одноподвижная (поступат. и вращат.), S=5, V класс.

При нулевой степени свободы кинематической цепи ни одно из звеньев не может двигаться относительно неподвижного звена (стойки) и кинематическая цепь превращается в ферму.

Кинематические цепи могут быть простыми и сложными.

У простой кинематической цепи каждое звено входит не более чем в две кинематические пары, у сложной пары каждое звено входит более чем в 2 кинематические пары (рисунок 1.2).

Простая КП Сложные КП

Рисунок 1.2 − Виды кинематических цепей

Простые и сложные кинематические цепи, в свою очередь, делятся на незамкнутые и замкнутые (рисунок 1.3).

Рисунок 1.3 − Кинематические цепи

а − простая (незамкнутая); б – сложная незамкнутая; в – простая замкнутая;

1, 2,….6 – звенья; А, В, ….., L − кинематические пары.

Число степеней свободы кинематической пары относительно неподвижного звена называется подвижностью кинематической цепи(механизма).

Подвижность пространственной цепи (механизма) определяется по формуле Сомова-Малышева

W=6n-5p5-4p4-3p3-2p2-p1, (1.3) где n-число подвижных звеньев,

p1…p5 – число пар I…V классов.

Подвижность плоского механизма уменьшается на 3 и рассчитывается по формуле Чебышева

W=3n - 2p5 - p4 (1.4)

При изучении структуры и кинематики плоских механизмов во многих случаях удобно заменять высшие пары механизмов низшими. При этом подвижность механизма не должна изменяться. Полученный механизм называется заменяющим (рисунок 1.4)

Рисунок 1.4 − Схема механизма с высшей парой

Представляемый подвижными звеньями 1,2 фрикционный механизм состоит из высшей кинематической пары 1,2 IV класса и двух низших пар 01 и 02 V класса и стойки, т.е. n=2, P₅=2, P₄=1. Подвижность такого механизма составляет

W=3n - 2p - p4=3 ·2 –2 ·2 -1=1, (1.5)

Заменяющий механизм представлен подвижными звеньями 1´2´3´ и стойками 0. Кинематические пары 01´; 1´,2´ 2´3´, 3´0 является вращательными парами пятого класса. Имеем n=3, p5=4, и p4=0

Тогда подвижность заменяющего механизма будет равна

W=3n - 2p5 - p4=3 ·3 –2 ·4 - 0=1, (1.6)

Таким образом, после замены высшей пары низшей подвижность механизма не изменилась, следовательно, замена выполнена правильно.

В современном машиностроении наиболее широкое распространение получили плоские механизмы, звенья которых входят в пары IV и V класса.

Задачей структурного анализа является построение структурной схемы, расчленение ее структурные единицы и определение класса групп Ассура и механизма в целом.

Любой механизм имеет одно неподвижное звено «стойку», начальное звено и присоединенные к ним цепи звеньев. Если механизм имеет одно начальное звено, степень его подвижности равна 1, если два начальных звена, подвижность равна 2 и т.д. Расчеты по формуле Чебышева дает те же результаты. Следовательно, присоединение к механизму последующих кинематических пар не меняет его подвижность, а значит, подвижность присоединенных пар должна быть равна 0.

Кинематическая цепь с нулевой степенью подвижности (свободы) относительно внешних кинематических пар, не распадающаяся на более простые цепи, называется группой Ассура (Wгр = 0).

Назовем условно начальное звено и стойку, образующие кинематическую пару пятого класса, механизмом первого класса. Тогда любой механизм состоит из механизма первого класса и присоединенных к нему групп Ассура.

Порядок группы Ассура определяется числом элементов звеньев, которыми группа присоединяется к основному механизму, а класс группы Ассура – наивысшим классом входящих в него контуров (таблица 1.1).

Таблица 1.1 − Классы и виды контуров

Класс всего механизма определяется наивысшим классом группы Ассура, входящей в данный механизм.

Структурный анализ механизма включает в себя:

1. Построение кинематической схемы механизма.

2. Нумерацию звеньев и обозначение буквами кинематических пар.

3. Подсчет подвижных звеньев и кинематических пар различного класса.

4. Определение подвижности механизма.

5. Построение структурной схемы механизма.

6. Расчленение механизма на структурные единицы.

7. Определение класса структурных единиц.

8. Определение класса всего механизма в целом.

Пример № 1. Выполнить структурный анализ рычажного механизма (рисунок 1.5).

Рисунок 1.5 − Схема рычажного механизма

Решение:

1. Обозначаем звенья цифрами (неподвижные 0, подвижные 1, 2, 3), а кинематические пары буквами (0, А, Б, 0).

2. Подсчитываем количество подвижных звеньев, имеем n = 3.

3. Определяем класс и число кинематических пар:

Все пары вращательные 5 класса, следовательно

Р₅ = 4 (0.1; 1,2; 2,3; 3,0)

4. Определяем степень подвижности механизма по формуле Чебышева

W = 3n – 2P₅ = 3 · 3 – 2 · 4 = 1, (1.7)

5. Строим структурную схему механизма (рисунок 1.6).

Рисунок 1.6 − Структурная схема рычажного механизма

 

6. Расчленяем механизм на структурные единицы и определяем их класс (рисунок 1.7).

Механизм 1-го класса Группа Ассура 2 класса, 2 порядка

Рисунок 1.7 − Структурные единицы

7. Определяем класс всего механизма в целом. Класс механизма определяется наивысшим классом группы Ассура. В данном случае в механизм входит группа Ассура 2 класса, следовательно, механизм в целом относится к механизму второго класса.

Пример № 2. Выполнить структурный анализ рычажного механизма, состоящего из пяти подвижных звеньев (рисунок 1.8).

Рисунок 1.8 − Кинематическая схема пятизвенного механизма

Структурный анализ удобнее выполнять, используя вспомогательную таблицу, имеющую вид:

Таблица 1.2 − Кинематические пары, звенья и класс пар

Кинемат. пары				1V	V	V1	V11
№№ звеньев	0,1	1,2	2,3	3,0	3,4	4,5	5,0
Класс

Из таблицы 1.2 следует, что: n=5, P₅=7.

Тогда подвижность механизма будет равна:

W = 3n - 2 P₅ = 3 · 5 – 2 · 7 = 1, (1.8)

Значит, механизм состоит из механизма первого класса и присоединенных к нему групп Ассура.

Строим структурную схему механизма и расчленяем на структурные единицы (рисунок 1.9).

Структурная схема Механизм 1 класса Группы Ассура 2 класса

Рисунок 1.9 − Структурные единицы рычажного механизма

Выводы: Механизм состоит из механизма первого класса и двух групп Ассура второго класса 2-го порядка. Следовательно, в целом механизм относится к механизму второго класса.

ЗАДАНИЯ 2

1        2. 3.                    4.   5.                   6. Контрольные вопросы

1. Что называется механизмом?

2. Как классифицируются кинематические пары?

3. Какие кинематические пары относятся к низшим и к высшим?

4. Как определяется подвижность механизма, формула?

5. Что называется группой Ассура?

6. Как определяется класс гр. Ассура?

7. Цель и принцип построения заменяющего механизма.

8. Какова цель структурного анализа механизма, последовательность действия при анализе?

9. Как определяется класс всего механизма в целом?

 

Практическая работа №4