
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость дискретных системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим устойчивость импульсных систем как класса дискретных САУ В общем случае свободное движение в замкнутой дискретной системе описывается разностным уравнением «n»-го порядка:
или соответствующим ему характеристическим уравнением:
Решение уравнения (1.14.1) имеет вид:
Zk – корни характеристического уравнения (1.14.2), qk – полюса ПФ Ф*(q) – ПФ замкнутой системы. В асимптотически устойчивой системе выполняются условия:
Из выражения (1.14.3) видно, что для устойчивости системы необходимо, чтобы вещественная часть полюсов была отрицательной Корни zk должны лежать внутри окружности единичного радиуса. Если хотя бы один из корней лежит на окружности, то система находится на границе устойчивости. Для того, чтобы можно было применить критерий устойчивости непрерывных систем переходят от z формы к W - форме. При этом характеристическое уравнение имеет 1.14.2 приобретает вид:
и необходимое условие устойчивости - положительность коэффициентов bi:
Для уравнения второго порядка необходимое условие является и достаточным. В случае устойчивой системы все корни zk (уравнение 1.14.2). лежащие внутри единичного круга, перейдут в левую полуплоскость W. Положительность коэффициента а i не является необходимым условием устойчивости. Покажем это на примере ЦСАУ с характеристическим уравнением замкнутой системы второго порядка:
Перейдем от z – формы к w форме – немодифицированное преобразование:
где коэффициенты bi определяются выражениями:
Условием устойчивости ИС будет положительность коэффициентов bi > 0, но не аi > 0. Пусть Необходимое условие устойчивости не выполняется, хотя исходное уравнение имеет все «+» коэффициенты. Вычислим корни исходного уравнения.
для устойчивости требуется Замкнутая ИС будет устойчива, если все корни wi уравнения (1.14.4) лежат в левой полуплоскости, т.е. выполняется условие После перехода к W- форме для исследования устойчивости дискретных систем можно применять критерии непрерывных систем. Однако, существуют специальные критерии устойчивости дискретных систем (аналоги критериев непрерывных систем). 1.14.2 Аналог критерия Михайлова Аналог критерия Михайлова для ИС основан на рассмотрении характеристического полинома:
Построим на плоскости q контур L, лежащий в правой части полосы
Рисунок 1.14.2
Предположим, что на самом контуре нет нулей и полюсов
где Ри N соответственно число полюсов и нулей функции
На отрезке мнимой оси
При изменении q вдоль отрезка L 2, при σ изменяющемся от При изменении q вдоль прямой L 4 от На бесконечно удаленном участке L 4 имеем
Подставляя найденные значения аргументов (1.14.8 - 1.14.11) в (1.14.7), получим Это необходимое и достаточное условие устойчивости импульсной системы. В силу симметричности если при этом то замкнутая ИС устойчива. Выражение (1.14.12) является аналогом критерия Михайлова для дискретных систем. Подставим в В крайних точках интервала
т.е. АФХ ИС в этих точках имеет вещественные значения. АФХ ИС
а) б) Рисунок 1.14.3 – Аналоги кривой Михайлова. Для системы третьего порядка случай устойчивой системы имеет вид а), неустойчивой системы – вид б). Аналог критерия Найквиста Рассмотрим ПФ разомкнутой импульсной системы:
Примем e=0 и введём вспомогательную функцию
где Из аналога критерия Михайлова следует, что для устойчивости замкнутой системы необходимо выполнение условия:
Возможны три случая состояния разомкнутой системы: Устойчивая разомкнутая система В этом случае по аналогу критерия Михайлова можно записать Поскольку замкнутая система должна быть устойчивой, то
а приращение аргумента вспомогательной функции
Т.е. годограф Таким образом, для устойчивости замкнутой системы, при устойчивой разомкнутой, необходимо и достаточно, чтобы годограф вспомогательной функции
Рисунок 1.14.4 В случае астатической системы степени ν также как и для непрерывных систем, годограф АФХ (рис.1.14.5) дополняется дугой бесконечного радиуса на угол
Рисунок 1.14.5
В случае неустойчивой разомкнутой системы уравнение Тогда приращение аргумента вспомогательной функции
Для устойчивости замкнутой системы при неустойчивой разомкнутой необходимо и достаточно, чтобы разность числа положительных и отрицательных переходов годографа АФХ (рисунок 1.14.6) через отрезок действительной оси (- 1; j 0) была равна
Рисунок 1.14.6 Например, если разомкнутая система неустойчива и
|
||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 985; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

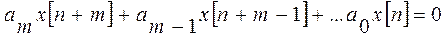 (1.14.1)
(1.14.1) (1.14.2)
(1.14.2) (1.14.3)
(1.14.3)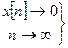 в установившемся режиме.
в установившемся режиме. , а
, а 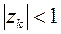 .
. , то система будет неустойчивой.
, то система будет неустойчивой. (1.14.4)
(1.14.4)
 .
.

 , тогда
, тогда  ,
,  ,
, 

 , а здесь
, а здесь 

 (1.14.5)
(1.14.5) и образованный отрезком мнимой оси L 1 , границами этой полосы L 2 и L 4, и бесконечно удаленным отрезком прямой L 3, параллельным мнимой оси (рисунок 1.14.2)
и образованный отрезком мнимой оси L 1 , границами этой полосы L 2 и L 4, и бесконечно удаленным отрезком прямой L 3, параллельным мнимой оси (рисунок 1.14.2)
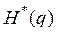 , тогда, на основании принципа аргумента при изменении q вдоль контура в отрицательном направлении, то есть так, чтобы область, ограниченная контуром L, оставалась справа, то приращение аргумента функции
, тогда, на основании принципа аргумента при изменении q вдоль контура в отрицательном направлении, то есть так, чтобы область, ограниченная контуром L, оставалась справа, то приращение аргумента функции  будет равно:
будет равно: (1.14.6)
(1.14.6) , лежащих в области ограниченной контуром L. Учитывая, что для
, лежащих в области ограниченной контуром L. Учитывая, что для  число полюсов Р=0, то для устойчивости замкнутой АИС необходимо и достаточно, чтобы в этой области отсутствовали нули функции
число полюсов Р=0, то для устойчивости замкнутой АИС необходимо и достаточно, чтобы в этой области отсутствовали нули функции  ,
,  (1.14.7)
(1.14.7) и поэтому
и поэтому . (1.14.8)
. (1.14.8) , до
, до  , функция
, функция 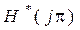 до значения
до значения 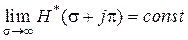 . (1.14.9)
. (1.14.9) до
до  в направлении противоположном предыдущему и, значит,
в направлении противоположном предыдущему и, значит,  . (1.14.10)
. (1.14.10) и приближенно
и приближенно 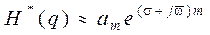 , а приращение аргумента
, а приращение аргумента (1.14.11)
(1.14.11) , откуда
, откуда  .
. относительно действительной оси можно рассмотреть интервал
относительно действительной оси можно рассмотреть интервал  ,
, , (1.14.12)
, (1.14.12) . (1.14.13)
. (1.14.13) и
и  получим
получим ,
,  ,
, - можно представить в виде вещественной и действительной части и в координатах Х, Y изобразить аналог кривой Михайлова.
- можно представить в виде вещественной и действительной части и в координатах Х, Y изобразить аналог кривой Михайлова.


 , (1.14.15)
, (1.14.15) - характеристический полином замкнутой системы,
- характеристический полином замкнутой системы,  - характеристический полином разомкнутой системы, порядки полиномов равны между собой и равны m.
- характеристический полином разомкнутой системы, порядки полиномов равны между собой и равны m.
 (1.14.16)
(1.14.16) .
.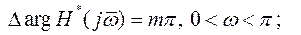

 не должен охватывать начало координат.
не должен охватывать начало координат. не охватывал начало координат, а соответствующий годограф АФХ
не охватывал начало координат, а соответствующий годограф АФХ  не охватывал точку
не охватывал точку 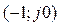 (рисунок 1.14.4).
(рисунок 1.14.4).
 , затем применяется предыдущий критерий.
, затем применяется предыдущий критерий. ν=1
ν=1 имеет l корней вне окружности единичного радиуса, то
имеет l корней вне окружности единичного радиуса, то  , при
, при 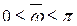 .
.
 .
.
 ), то согласно рис.1.14.6 замкнутая ИС будет устойчива.
), то согласно рис.1.14.6 замкнутая ИС будет устойчива.


