
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические ошибки дифференцирования⇐ ПредыдущаяСтр 16 из 16
Рассмотрим методическую ошибку получения первой производной стационарного случайного сигнала g (t),обладающего свойством эргодичности. Для этого сигнала можно найти следующие функции: корреляционную функцию корреляционную функцию первой производной: взаимную корреляционную функция где М – математическое. ожидание. Ошибка определения первой производной в дискретные моменты времени может быть определена как разность между действительным и машинным значениями производной.
Возведем левую и правую часть этого выражения в квадрат и, определяя математическое ожидание, получим выражение средней квадратичной ошибки или дисперсии:
Если mg = 0, то R (0) = σg 2. Относительная ошибка вычисления СКО:
где Для гармонического сигнала:
Если математическое ожидание g (t) равно нулю, то при С учетом выражения (2.15.3.2) для произвольного числа m, учитываемых обратных разностей приближенно можно записать:
Полученное выражение позволяет выбрать период дискретности Т по заданному значению методической ошибки δМ, при известном значении числа слагаемых m или, наоборот, определить число слагаемых, при заданных методической ошибке и периоду дискретности Т.
Приближенную оценку (2.15.3.13) можно распространить на случай сигнала произвольной формы. Пусть непрерывный входной сигнал имеет (m +1) производных, а в алгоритме дифференцирования используются обратные разности
Приближенно можно записать:
Тогда
Возведя в квадрат левую и правую части этого выражения и переходя к математическому ожиданию получаем СКО по дифференцированию.
где
При mg = 0:
Влияние шумов квантования
Квантование по уровню вызывает появление дополнительной ошибки, носящей случайный характер. На выходе АЦП появляется дискретный сигнал, содержащий l шагов квантования q. (рисунок 2.15.4.1)
Δq – абсолютная ошибка квантования. Рисунок 2.15.4.1
Остаток ∆ q обычно округляют до ближайшего сверху или снизу к значению gq целому числу. Будем предполагать, что величина ошибки генерируется быстроменяющимся сигналом, который можно рассматривать как белый шум, плотность распределения вероятности которого имеет вид: (рисунок 2.15.4.2)
Рисунок 2.15.4.2
Среднее значение:
Дисперсия определяется как математическое ожидание квадрата разности:
Корреляционная функция белого шума представляет собой δ-функцию. поэтому корреляционная функция ошибки квантования может быть представлена:
Тогда для дискретных моментов времени случайные ошибки квантования можно считать взаимно-независимыми, что позволяет определить дисперсию результирующей ошибки квантования при вычислении производной путем суммирования дисперсий ошибок квантования в дискретные моменты времени. В случае вычисления первой производной суммарная дисперсия ошибки округления имеет вид:
где
Цифровые интеграторы Рассмотрим алгоритмы цифрового интегрирования решетчатых функций, соответствующие Однако практически рассматриваются только первые слагаемые в этих формулах. Использование последних слагаемых в выражениях (2.15.1.1), (2.15.1.2) приводит к неустойчивому алгоритму, а выражение (2.15.1.3) к неустойчивым алгоритмам не приводит, но ничего не дает практически в части увеличения точности интегрирования. В результате получим
Оператор интегрирования:
Из выражений (2.15.5.1), (2.15.5.2), (2.15.5.3) можно получить разностные уравнения, определяющие алгоритм интегрирования для машинной переменной:
В выражениях (2.15.5.6), (2.15.5.8), (2.15.5.10), используется настоящие и прошлые значения входного сигнала g [ n ] и прошлые значения сигнала fM [ n ]. Прошлые значения сигнала хранятся в памяти ЭВМ и эти выражения могут использоваться в реальном масштабе времени. При интегрировании постоянного во времени сигнала формулы (2.15.5.1), (2.15.5.2), (2.15.5.3) дают нулевую ошибку. Для определения ошибки при интегрировании сигнала другой формы вводят в рассмотрение ошибку интегрирования на шаге.
Изображение обратной разности:
Тогда изображение ошибки интегрирования на шаге:
F (z) – изображение функции FM (z) – машинное значение интеграла. Применив к (2.15.5.13) обратное z –преобразование получим, что ошибка на шаге:
Общая ошибка интегрирования может быть найдена суммированием ошибки на шаге по всем шагам.
Рассмотрим пример: Входной сигнал
При интегрировании линейно возрастающего сигнала суммарная ошибка интегрирования может быть найдена умножением постоянной ошибки на шаге на число шагов N = t / T.
t – интервал интегрирования.
Цифровые фильтры Предмет цифровой фильтрации данных (сигналов) является естественным введением в широкую и фундаментальную область цифровой обработки информации. Под фильтрацией будем понимать любое преобразование информации (сигналов, результатов наблюдений), при котором во входной последовательности обрабатываемых данных целенаправленно изменяются определенные соотношения (динамические или частотные) между различными компонентами этих данных. К основным операциям фильтрации информации относят операции сглаживания, прогнозирования, дифференцирования, интегрирования и разделения сигналов, а также выделение информационных (полезных) сигналов и подавление шумов (помех). Как известно, преобразование динамики сигналов (и данных, которые несут эти сигналы) осуществляется в системах. Соответственно, фильтры с любым целевым назначением являются частным случаем систем преобразования сигналов, в рамках теории которых они и будут рассматриваться. В настоящем разделе рассматриваются, в основном, методы линейной обработки данных (носителей этих данных - сигналов) линейными дискретными системами. Линейными называют системы, которые осуществляют преобразование линейных комбинаций входных сигналов в суперпозицию выходных сигналов. Принцип реализации линейных систем, физический - в виде специальных микропроцессорных устройств, или алгоритмический - в виде программ на ЭВМ, существенного значения не имеет и определяет только их потенциальные возможности.
Цифровые фильтры (ЦФ) представляют собой цифровое устройство, реализующее алгоритм:
x [ n ], y [ n ] – «n»-ые отсчеты входного Х и выходного У сигналов. aj и bi – коэффициенты. Поскольку операция умножения отсчетов цифрового сигнала на число часто выполняется неточно за счет округлений или усечений произведений, то в общем случае ЦФ не точно реализуют алгоритм (2.16.1). Однако в ЦФ, по сравнению с аналоговыми, погрешность выходного сигнала не зависит от условий, при которых работает фильтр (температура, влажность и т.д.). Кроме того, эта погрешность контролируема, т.е. ее можно уменьшить путем увеличения числа разрядов для построения отсчетов цифрового сигнала. Достоинства ЦФ по сравнению с аналоговыми: 1. Высокая точность обработки сигналов и стабильность характеристик. 2. Возможность реализации алгоритмов и операций принципиально невозможных в аналоговых. Например, обработка инфранизкочастотных сигналов, поскольку длительность хранения информации Ц. элементами практически неограниченна. Недостатки ЦФ: 1. Относительно низкая скорость обработки информации, вследствие задержек цифровых элементов. 2. Относительно большая стоимость. 3. Необходимость использовать на входе и выходе АЦП и ЦАП, что уменьшает быстродействие и точность.
Нерекурсивные фильтры Выражение (2.16.1) описывает алгоритм рекурсивного ЦФ. При нулевых значениях коэффициентов а j – выражение (2.16.1) переходит в уравнение линейной дискретной свертки переменной x [ n ] с оператором bi.
Выражение (2.16.2) показывает, что выходные отсчеты y [ n ] определяются текущим и прошлым значениями входных отсчетов. Такой фильтр называется нерекурсивным ЦФ (НЦФ). Интервал суммирования i получил название окна. Окно фильтра составляет N +1 отсчет. Фильтр является односторонним (каузальным) т.е. причинно обусловленным текущим и прошлым значениями входного сигнала и выходной сигнал не опережает входной. Каузальный фильтр может быть реализован в реальном масштабе времени.
При n < i, а также для выражения (2.16.1) n < j проведение фильтрации возможно лишь при задании начальных условий
При N ’= N фильтр называют двусторонним симметричным. Симметричные фильтры в отличие от односторонних не изменяют фазы обрабатываемого сигнала. Техника выполнения фильтрации иллюстрируется следующим примером.
Представим, что на одной полоске бумаги выписаны по порядку сверху вниз значения данных xn. На второй полоске записаны в обратном порядке значения bi. Для вычисления yn расположим вторую полоску напротив первой таким образом, чтобы b 0 находился напротив xn. Перемножаем все значения bi с расположенными против них значениями xn - i, и суммируем все результаты перемножения. Результат суммирования является выходным значением сигнала yn. Сдвигаем окно фильтра - полоску коэффициентов bi, на один отсчет последовательности х n вниз (или массив х n сдвигаем на отсчет вверх) и вычисляем аналогично следующее значение выходного сигнала, и т.д. Перемножаем все и суммируем (рисунок 2.16.1).
Рисунок 2.16.1
y [ n ] = b 0 x [ n ] + b 1 x [ n -1] + b 2 x [ n -2]; (2.16.4) y[n+1] = b0x[n+1] + b1x[n] + b2x[n-1]. (2.16.5) Описанный процесс является основной операцией цифровой фильтрации, и называется сверткой в вещественной области массива данных xn с функцией (оператором) фильтра bi (массивом коэффициентов фильтра). Сумма коэффициентов фильтра определяет коэффициент передачи (усиления) средних значений сигнала в окне фильтра и постоянной составляющей в целом по массиву данных (с учетом начальных и конечных условий). Как правило, сумма коэффициентов фильтра нормируется к 1. Имеется целый ряд методов обработки данных, достаточно давно и широко известных, которые по существу относятся к методам цифровой фильтрации, хотя и не называются таковыми. Например, методы сглаживания отсчетов в скользящем окне постоянной длительности. Для линейного сглаживания данных по пяти точкам с одинаковыми весовыми коэффициентами используется формула: y [ n ] = 0.2(xn -2 + xn -1 + xn + xn +1 + xn +2); b 0 = 0.2; С позиций цифровой фильтрации это не что иное, как двусторонний симметричный нерекурсивный цифровой фильтр:
Сумма коэффициентов, сглаживающих нерекурсивных ЦФ всегда должна быть равна единице. Х n = (0,0,0,0,0,0,0,10,10,10,10,0,0,0…). Уравнение НЦФ имеет вид (2.16.6) Выходной сигнал: y n = (0,0,0,0,2,4,6,8,8,6,4,2,0…).
Результат фильтрации приведен на рисунке 2.16.2.
Рисунок 2.16.2 Координатная детальность выходного сигнала ниже входного, резкие изменения входных сигналов «размазываются» по аргументу. В случае конечной функции х n функция у n также конечна. Нерекурсивные ЦФ относят к классу фильтров с конечной импульсной характеристикой (КИХ). Рекурсивные фильтры Описываются выражением:
Эти фильтры называют также фильтрами с обратной связью, т.к. в вычислениях текущих выходных значений участвуют не только входные данные, но и значения выходных данных фильтрации, вычисленных в предшествующих циклах расчета. Обратная связь может быть отрицательной или положительной в зависимости от знака суммы коэффициентов aj. Полное окно РФ состоит из прошлых и текущих значений входного сигнала и прошлых значений выходного сигнала. Техника вычислений для рекурсивного фильтра иллюстрируется: (рисунок 2.16.2.1). Уравнение РЦФ
Рисунок 2.16.2.1 Расчет значений выходного сигнала производится по выражениям: y[n] = b0x[n] + b1x[n-1] + b2x[n-2]+ b3x[n-3]- a1y[n-1]- a2y[n-2]; y[n+1] = b0x[n+1] + b1x[n] + b2x[n-1]+ b3x[n-2]- a1y[n]- a2y[n-1]; Пример. Уравнение РЦФ:
Расчёт выходного сигнала:
Результат фильтрации представлен на рисунке 2.16.2.2.
Рисунок 2.16.2.2 Из примера видно, что реакция РЦФ на конечный входной сигнал, в принципе, может иметь бесконечную длительность (с близкими к нулю, но ненулевыми значениями. В отличие от реакции НЦФ, которая всегда ограничена количеством членов bi (окном фильтра). РЦФ относятся к классу БИХ (бесконечной импульсной характеристикой). Передаточная функция РЦФ:
ПФ НЦФ W (Z) имеет вид конечного степенного полинома и, формально, равна числителю (2.16.2.2).
При расчете ЦФ нередко используется сначала расчет ПФ аналогового фильтра, затем известными методами определяют ПФ ЦФ в z-форме.
|
|||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.200.66 (0.074 с.) |
 ,
, ,
, ,
, (2.15.3.1)
(2.15.3.1)
 (2.15.3.3)
(2.15.3.3) – ошибка машинного времени;
– ошибка машинного времени; 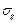 – среднеквадратическое значение скорости (первой производной сигнала g (t)).
– среднеквадратическое значение скорости (первой производной сигнала g (t)).
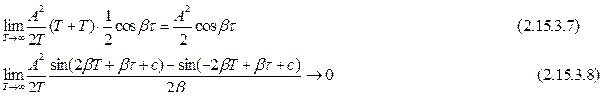

 .
.
 (2.15.3.14)
(2.15.3.14) Оценим ошибку от отбрасывания не равной нулю обратной разности
Оценим ошибку от отбрасывания не равной нулю обратной разности  Ошибка дифференцирования пропорциональна отбрасываемому члену.
Ошибка дифференцирования пропорциональна отбрасываемому члену. .
.
 .
.
 – среднеквадратическое значение производной входного сигнала,
– среднеквадратическое значение производной входного сигнала, – СКО первой производной.
– СКО первой производной.


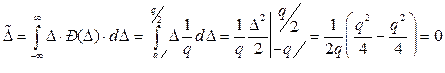 (2.15.4.1)
(2.15.4.1) (2.15.4.2)
(2.15.4.2)
 – единичная решетчатая функция.
– единичная решетчатая функция. (2.15.4.3)
(2.15.4.3) . Операция интегрирования в операторном виде представляется как
. Операция интегрирования в операторном виде представляется как  , т.е. является обратной операции дифференцирования и может быть получена из выражений (2.15.1.1), (2.15.1.2), (2.15.1.3) их переворачиванием.
, т.е. является обратной операции дифференцирования и может быть получена из выражений (2.15.1.1), (2.15.1.2), (2.15.1.3) их переворачиванием.
 (2.15.5.3)
(2.15.5.3) (2.15.5.4)
(2.15.5.4) (2.15.5.5)
(2.15.5.5) (2.15.5.6)
(2.15.5.6)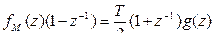 (2.15.5.7)
(2.15.5.7) (2.15.5.8)
(2.15.5.8) (2.15.5.9)
(2.15.5.9) (2.15.5.10)
(2.15.5.10) (2.15.5.11)
(2.15.5.11) (2.15.5.12)
(2.15.5.12) (2.15.5.13)
(2.15.5.13) .
. (2.15.5.14)
(2.15.5.14) (2.15.5.15)
(2.15.5.15)
 (2.15.5.16)
(2.15.5.16) (2.16.1)
(2.16.1) (2.16.2)
(2.16.2) . Как правило, в качестве начальных условий принимают нулевые значения. При обработке данных на ЭВМ ограничения по каузальности снимаются. В памяти фильтра могут храниться, как прошлые, так и будущие значения входной последовательности отсчетов относительно текущей точки вычисления i. При этом уравнение (2.16.2) имеет вид:
. Как правило, в качестве начальных условий принимают нулевые значения. При обработке данных на ЭВМ ограничения по каузальности снимаются. В памяти фильтра могут храниться, как прошлые, так и будущие значения входной последовательности отсчетов относительно текущей точки вычисления i. При этом уравнение (2.16.2) имеет вид: . (2.16.3)
. (2.16.3)

 (2.16.6)
(2.16.6)
 (2.16.2.1)
(2.16.2.1)

 ;
;  ;
;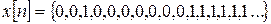


 (2.16.2.2)
(2.16.2.2)



