
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная помехоустойчивость различныхСодержание книги Поиск на нашем сайте
Видов дискретной модуляции 1. Дискретная амплитудная модуляция. S 1 (t) = A cos w0 t, S 2 (t) = 0, 0 < t < T; E э =
Подставив эту величину в формулу ( 7.6 ), получим
2. Дискретная частотная модуляция. S 1 (t) = A co s w1 t; S 2 (t) = A co s w2 t, 0 < t < T. E э = = E 1 + 2 TBS1S2(0) + E 2. При частотной модуляции сигналы S 1 (t) и S 2 (t) являются взаимоортогональными, поэтому их функция взаимной корреляции равна нулю. Кроме того, благодаря равной амплитуде сигналов S 1 (t) и S 2 (t) E 1= E 2. В результате E э = 2 E 1 , а Подставив эту величину в формулу ( 7.6 ), получим
3. Дискретная фазовая модуляция S 1 (t) = A co s w 0 t, S 2 (t) = - A cos w0 t = - S 1 (t), 0 < t < T;
Подставив эту величину в формулу ( 7.6 ), получим
Сравнивая между собой формулы ( 8.1 ), ( 8.2 ), ( 8.3 ), видим, что для достижения заданной вероятности ошибки при ДЧМ требуется величина h0 в Из рис. 8.1 видно, что при ДАМ расстояние между векторами сигналов S 1 и S 2 равно длине вектора S 1, при ДЧМ ( взаимоортогональные сигналы ) это расстояние равно Следует заметить, что приведенные здесь данные об энергетике сигналов ДАМ, ДЧМ и ДФМ относились к максимальным ( пиковым ) мощностям этих сигналов. В этом смысле, например, при переходе от ДЧМ к ДАМ мы имеем двухкратный выигрыш в пиковой мощности.
Однако, сигналы ДАМ имеют пассивную паузу ( мощность сигнала в паузе равна нулю ), поэтому по потребляемой передатчиком мощности, кроме отмеченного ранее проигрыша, имеется еще и двухкратный выигрыш. С учетом этого обстоятельства, при переходе от ДЧМ к ДАМ двухкратный проигрыш по пиковой мощности компенсируется двухкратным выигрышем за счет пассивной паузы сигналов ДАМ, в результате чего по потребляемой мощности эти сигналы оказываются равноценными. Однако следует помнить, что при ДАМ в приемнике Котельникова трудно установить необходимый порог в сравнивающем устройстве, а в приемнике ДЧМ регулировка порога не требуется. Поэтому частотная модуляция применяется чаще, чем амплитудная.
Отметим еще раз, что приемник Котельникова обеспечивает наибольшую предельно-допустимую ( потенциальную ) помехоустойчивость. Это достигается благодаря тому, что при приеме учитываются все параметры сигнала, не несущие информации: амплитуда, частота, фаза несущего колебания, а также длительность сигнала Т, так как интегрирование ( фильтрация ) осуществляется в течение этого времени. Решение о принятом сигнале обычно осуществляется в конце каждого интервала Т, для чего в приемнике должна иметься специальная система синхронизации элементов сигнала.
9. Оптимальная фильтрация дискретных сигналов Оптимальный приемник (рис.6.1) является корреляционным, сигнал на его выходе представляет собой функцию корреляции принимаемого сигнала x(t) и ожидаемого Si(t), благодаря чему обеспечивается максимально - возможное отношение сигнал/шум h20..
Поскольку операция определения функции корреляции является линейной, ее можно реализовать в некотором линейном фильтре, характеристики которого (комплексная передаточная характеристика K(jw) и импульсная характеристика g(t) являются такими, что отношение сигнал/шум на его выходе получается максимальным, причем h2max = h20. Найдем характеристики фильтра, когда помеха n(t) является флюктуационной со спектральной плотностью Gn(w) = N0,, w ³ 0. Пусть сигнал на входе фильтра имеет комплексный спектр S(jw). Тогда сигнал на выходе фильтра y(t) можно определить с помощью преобразования Фурье
Нас интересуют значение y(t) в момент принятия решения (момент отсчета t0), поэтому, заменив t на t0, получим
Чтобы получить максимальную величину y(t0), нужно найти оптимальную характеристику фильтра k(jw). Для этой цели можно воспользоваться известным неравенством Шварца-Буняковского, имеющим вид
Легко проверить, что данное неравенство превращается в равенство при условии,что
где a - любая произвольная постоянная. В нашем случае, применительно к формуле (9.1), величина y(t0) будет максимальной при условии
(это уже есть условие оптимальности характеристики K(jw), поэтому здесь и в дальнейшем K(jw) заменено на Kopt(jw)).
Подставляя в левую часть формулы (9.2)
получаем
или, сокращая на S(w), будем иметь
Последнюю формулу можно представить в виде двух составляющих, позволяющих найти амплитудно-частотную характеристику оптимального фильтра Kopt(w) и фазо-частотную характеристику jk(w):
откуда Здесь js(w) - фазо-частотный спектр входного сигнала; wt0 - "запаздывающий" множитель, учитывающий то, что "отсчет" величины сигнала на выходе фильтра производится в момент t0, когда возникает максимум выходного сигнала фильтра. Условие (9.6) имеет простой физический смысл: фильтр должен лучше пропускать составляющие спектра сигнала, имеющие большую амплитуду и в меньшей степени пропускать составляющие сигнала, имеющие меньшую амплитуду. Условие (9.7) имеет также простой физический смысл: в момент отсчета (t0) все частотные составляющие спектра выходного сигнала имеют нулевую фазу, благодаря чему выходное напряжение в момент t0 имеет наибольшее отношение мощности сигнала к мощности помехи. Условия (9.6) и (9.8) можно объединить в одно, представив передаточную характеристику в комплексной форме
Можно, наконец, последнюю формулу представить в следующем виде
Здесь S*(jw) - комплексно-сопряженный спектр по отношению к S(jw). Отношение сигнал/помеха определяется, как обычно, формулой
где
мощность (дисперсия) помехи на выходе фильтра, Dfopt - эффективная полоса пропускания оптимального фильтра. Подставляя в (9.11) выражения (9.1) и (9.12) с учетом (9.2), получим
где Из (9.13) видно, что отношение h2(t0) численно равно отношению энергии сигнала к спектральной плотности помехи (как в приемнике Котельникова) и не зависит от формы сигнала. А так как энергия сигнала равна произведению мощности сигнала на его длительность, то для повышения помехоустойчивости систем связи с использованием согласованных фильтров можно увеличивать длительность элементарных сигналов, что и делается в широкополосных системах связи. При применении в демодуляторе приемника согласованных фильтров в сочетании с когерентным способом приема можно добиться потенциальной помехоустойчивости. Импульсная характеристика оптимального фильтра (отклик фильтра на дельта-функцию) определяется известным выражением
Подставив сюда значение Kopt(jw) из (9.10), получим
Интегрирование в последней формуле производится по всем частотам от -¥ до +¥; поэтому знак перед w в этой формуле можно заменить на противоположный, что не приведет к изменению результата вычисления интеграла. В результате получим
А так как, на основании преобразования Фурье
то, сравнивая (9.14) и (9.15), получаем
Таким образом, функция g(t) отличается от сигнала S(t) только постоянным множителем а, смещением на величину t0 и знаком аргумента t (то есть функция g(t) является зеркальным отображением сигнала S(t), сдвинутым на величину t0. На рис. 9.2 в качестве примера приведен некоторый сигнал S(t), зеркально перевернутый сигнал S(- t) и функция g(t) = aS(t0 - t).
Как уже говорилось, величину t0 обычно берут равной длительности сигнала Т. Если взять t0 < T, то получается физически неосуществимая система (отклик начинается раньше поступления входного воздействия).
Сигнал y(t) на выходе линейной системы при поступлении на ее вход сигнала x(t) определяется известным интегралом Дюамеля
Пусть на вход оптимального фильтра поступает аддитивная смесь, содержащая сигнал S(t), с которым фильтр согласован, и помеха n(t) (это может быть флюктуационная помеха или какой-нибудь детерминированный сигнал, с которым фильтр не согласован) x(t)=S(t)+n(t), Подставляя x(t) и (9.16) в (9.17), получим
заменяя t0 на Т, получим
Таким образом, на выходе согласованного фильтра получаем под действием сигнала функцию корреляции сигнала, а под действием помехи функцию взаимной корреляции сигнала и помехи. Если на входе фильтра только помеха(без сигнала), на выходе получаем только функцию взаимной корреляции помехи и сигнала, с которым фильтр согласован. В формуле (9.19) а - любой произвольный множитель, поэтому произведение а Т можно заменить на произвольный множитель b. В момент времени t=T (момент отсчета) формула (9.19) дает
Примечание. Если на вход согласованного фильтра поступает флюктуационная помеха, то теоретически функция взаимной корреляции Bsn(0) должна быть равна нулю, так как сигнал и помеха являются независимыми функциями времени. Однако на практике Bsn¹ 0, так как при вычислении функции взаимной корреляции требуется бесконечно большое время интегрирования. В нашем же случае интегрирование ведется за время, равное Т. Поэтому формулы (9.19) и (9.20) являются приближенными. Результаты фильтрации не зависят от формы сигнала. Следовательно фильтр может быть применен и без детектора. Тогда оптимальный приемник полностью известных сигналов (рис. 6.1) может быть реализован в виде двух согласованных фильтров - СФ 1 , СФ 2 и устройства сравнения - УС (рис.9.3).
Примеры согласованных фильтров. Рассмотрим согласованный фильтр для прямоугольного импульса длительности Т (рис 9.4 а). Спектральная плотность такого импульса равна
Для согласованного фильтра, в соответствии с (9.10) для случая t0 = T
Пользуясь последним выражением, можно легко построить схему фильтра для данного случая. Так из теории электрических цепей известно, что деление на jw означает интегрирование сигнала, а множитель е-jwT означает задержку сигнала на время Т. В результате схема фильтра будет содержать интегратор, линию задержки и вычитатель (рис. 9.4). Таким образом, на выходе фильтра получился треугольный импульс с основанием 2Т (это - функция корреляции входного импульса прямоугольной формы). То, что выходной импульс имеет в два раза большую длительность, чем входной, является недостатком оптимального фильтра, так как "хвост" выходного сигнала на отрезке времени от Т до 2Т будет накладываться на выходной сигнал следующего импульса. Поэтому на практике часто применяют упрощенную схему фильтра, содержащую интегриру ющую RC -цепь (RC>> T) и ключ К (рис. 9.5).
В момент T окончания входного импульса ключ К замыкается, конденсатор интегратора быстро разряжается через ключ и схема оказывается готовой к приему следующего импульса.
Оптимальный фильтр для приема радиоимпульсов с прямоугольной огибающей может быть построен аналогичным образом, однако RC - цепочка должна быть заменена колебательным контуром с достаточно высокой добротностью. Фильтры с ключами называются "кинематическими" фильтрами.
|
||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.217.13 (0.01 с.) |

 S 21 (t) d t = E 1 (E э равна энергии первого сигнала );
S 21 (t) d t = E 1 (E э равна энергии первого сигнала );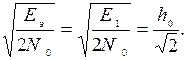
 ( 8.1 )
( 8.1 )
 ( 8.2 )
( 8.2 )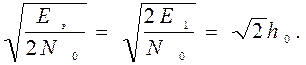
 ( 8.3 )
( 8.3 ) больше, чем при ДФМ, а при ДАМ - в 2 раза больше, чем при ФМ. Отсюда видно, что переход от ДАМ к ДЧМ дает двухкратный выигрыш по мощности, а к ДФМ - четырехкратный выигрыш. Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции.
больше, чем при ДФМ, а при ДАМ - в 2 раза больше, чем при ФМ. Отсюда видно, что переход от ДАМ к ДЧМ дает двухкратный выигрыш по мощности, а к ДФМ - четырехкратный выигрыш. Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляции.




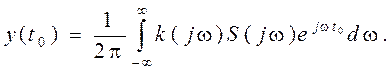 (9.1)
(9.1)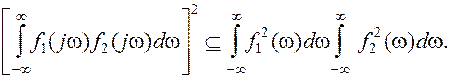

 (9.2)
(9.2)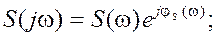 (9.3)
(9.3) (9.4)
(9.4)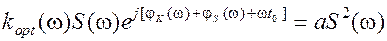
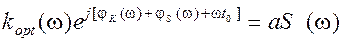 . (9.5)
. (9.5) ; (9.6)
; (9.6) (9.7)
(9.7) (9.8)
(9.8)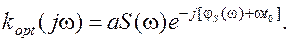 (9.9)
(9.9) (9.10)
(9.10)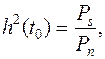 (9.11)
(9.11) - мощность сигнала на выходе фильтра в момент t0;
- мощность сигнала на выходе фильтра в момент t0; (9.12)
(9.12) (9.13)
(9.13) энергия сигнала S(t) на входе фильтра.
энергия сигнала S(t) на входе фильтра.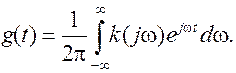

 (9.14)
(9.14)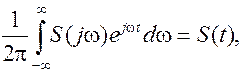 (9.15)
(9.15) (9.16).
(9.16).
 . (9.17)
. (9.17) , (9.18)
, (9.18)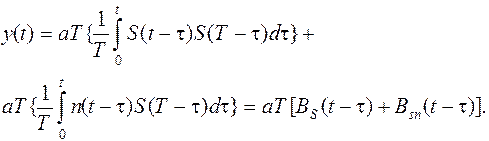 (9.19)
(9.19) (9.20)
(9.20)
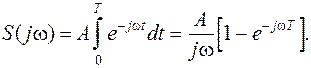 .
. (9.21)
(9.21)




