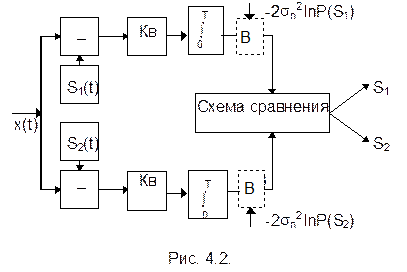Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальный приемник полностью известных сигналовСодержание книги
Поиск на нашем сайте
Рассмотрим систему связи, в которой передаются два сигнала S1(t) и S2(t) одинаковой длительности Т, произвольной (но известной) формы, априорные вероятности передачи Р(S1) и P(S2); помехи в канале связи флюктуационные, функция плотности распределения которых имеет гауссовский закон распределения вида
где s n 2 - дисперсия (мощность) помех. Задан критерий оптимального приема: идеальный наблюдатель (или наблюдатель В.А.Котельникова), который минимизирует среднюю вероятность ошибки Рош = P(S1)P(y2/S1) + P(S2)P(y1/S2). Найдем оптимальное правило решения и структурную схему оптимального приемника(оптимального РУ) для указанных выше условий передачи сигналов S1(t) и S2(t). 1. Для решения задачи используем общее для приемников двоичных сигналов правило решения (3.7). В рассматриваемом случае l0 = P(S2)/P(S1), (4.2) если l(x) > l0, то принимается решение в пользу сигнала S1,иначе - S2. Для упрощения решения положим вначале, что P(S1)= P(S2) = 0,5; тогда l0= 1. В этом случае критерий идеального наблюдателя совпадает с критерием максимального правдоподобия. 2. Для определения функций правдоподобия w(x/S1) и w(x/S2) предположим, что на вход приемника поступает сигнал x(t) = S1(t) + n(t), например, вида рис. 4.1.
Возьмем n отсчетов сигнала x(t) через одинаковые интервалы Dt, равные интервалу корреляции помехи t0n. Рассмотрим отсчетные значения суммы сигнала S1(t) и помехи n(t) в различных сечениях t i. Так как расстояние между сечениями равно интервалу корреляции помехи, эти сечения некоррелированы между собой. А так как помеха распределена по гауссовскому закону (4.1), то эти сечения также и независимы.
В 1-ом сечении x(t1) = S1(t1) + n(t1); в 2 -ом сечении x(t2) = S1(t2) + n(t2); - - - - - - - - - - - - - - - - - - - - - - - - - в k -ом сечении x(tk) = S1(tk) + n(tk). Возьмем n отсчетов сигнала x(t) через одинаковые интервалы Dt, равные интервалу корреляции помехи t0n. Рассмотрим отсчетные значения суммы сигнала S1(t) и помехи n(t) в различных сечениях t i. Так как расстояние между сечениями равно интервалу корреляции помехи, эти сечения некоррелированы между собой. А так как помеха распределена по гауссовскому закону (4.1), то эти сечения также и независимы. Плотность вероятности случайной величины х в k-м сечении при известном сигнале S1(tk) определяется выражением
Аналогичное выражение можно записать для сигнала S2, заменив в последнем выражении S1 на S2. Тогда отношение правдоподобияl(x)=
Прологарифмируем это выражение - или в другом виде
Таким образом, оптимальный приемник (идеальный приемник Котельникова) работает следующим образом: определяется среднеквадратическое отклонение поступившего на его вход сигнала x(t) от обоих ожидаемых сигналов (S1(t) и S2(t)) и выносится решение в пользу того сигнала, где это среднеквадратическое отклонение меньше. Если при вычислении условных вероятностей расстояние между сечениями Dt устремить к нулю, т. е. сделать Dt меньше интервала корреляции помехи, работа приемника не улучшится, так как соседние сечения будут сильно коррелированы, но и не ухудшится. Поэтому в правиле решения (4.3) можно заменить суммирование интегрированием. В интегральной форме получим
или более компактно (пунктир означает усреднение по времени) _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ [x(ti) - S1(ti)]2 < [x(ti) - S2(ti)]2, то S1. (4.4) В соответствии с полученным правилом решения структурная схема приемника будет иметь вид, приведенный на рис. 4.2. Схема содержит два генератора опорных сигналов S1(t) и S2(t), которые генерируют точно такие же сигналы, которые могут поступить на вход приемника, а также два вычитающих устройства, два квадратора, два интегратора и схему сравнения, которая, в соответствии с (4.4), выдает сигналы S1 или S2. При этом следует подчеркнуть, что приемник Котельникова, как и многие другие приемники дискретных сигналов, выдает на выходе сигналы S1 и S2, форма которых обычно отличается от формы сигналов в линии связи S1(t) и S2(t). Например, в линии связи эти сигналы могут представлять собой импульсы дискретной частотной модуляции, а на выходе приемника получаем импульсы постоянного тока прямоугольной формы.
Если вероятности передачи сигналов S1(t) и S2(t) не одинаковы, т.е. P(S1)¹ P(S2), то неравенство (4.4) принимает несколько другой вид _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ [x(ti) - S1(ti)]2 - 2s2n lnP(S1) < [x(ti) - S2(ti)]2 - 2s2n lnP(S1), то S1, (4.5) а в структурной схеме рис.4.2 перед схемой сравнения добавляются выравнивающие устройства - В (показаны пунктиром). Может показаться, что приведенная на рис.4.2 схема приемника достаточно проста. Однако применяющиеся в схеме местные генераторы S1(t) и S2(t) должны выдавать сигналы по форме идентичные передаваемым сигналам, ожидаемым на входе приемника; поэтому эти генераторы должны синхронизироваться приходящими сигналами, а это сделать довольно трудно.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

 , (4.1)
, (4.1)
 , а k -мерная плотность вероятности, благодаря независимости сечений, будет равна произведению одномерных плотностей вероятности различных сечений
, а k -мерная плотность вероятности, благодаря независимости сечений, будет равна произведению одномерных плотностей вероятности различных сечений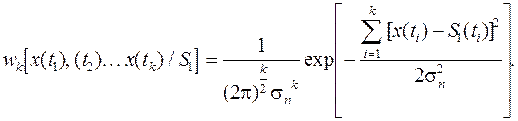 .
. и, согласно правилу решения (3.7), если вычисленное значение l(х) > 1 (у нас l0 = 1), то приемник должен выдать сигнал S1, в противоположном случае - сигнал S2. Отсюда получаем оптимальное правило решения в виде неравенства
и, согласно правилу решения (3.7), если вычисленное значение l(х) > 1 (у нас l0 = 1), то приемник должен выдать сигнал S1, в противоположном случае - сигнал S2. Отсюда получаем оптимальное правило решения в виде неравенства , то S1 .
, то S1 . [x(t i) - S1(ti)]2 +
[x(t i) - S1(ti)]2 +  [x(ti) - S1(ti)]2 dt <
[x(ti) - S1(ti)]2 dt <