
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая иллюстрация неопределенного интегралаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рис. 1
Задача 1. В следующих равенствах заполнить пропущенные места по соображению: 1) 2) 3) 4) 5) 6) Найти затем интегралы Построить интегральные кривые для пунктов 1 и 2. Решение. Рассмотрим выполнение 1 пункта:
Замечание. Интеграл Интегральные кривые:
Остальные пункты задачи выполняются аналогично. Задача 2. Найти интеграл: Решение. 1. Используя свойство (5), распишем интеграл алгебраической суммы нескольких слагаемых в виде суммы интегралов от каждого слагаемого:
2. По свойству (4) во втором слагаемом постоянный коэффициент 3 вынесем за знак интеграла. Используем формулы (2), (3) (Т.И.).
Задача 3. Найти интеграл:
Замечание. Если подынтегральные функции содержат выражения вида
Решение.
Задача 4. Найти интегралы: 1) 2) Указание. Выполнить по образцу задачи 3, используя свойства (5), (4) и формулы (1), (2), (3) (Т.И.).
Задача 5. Найти интеграл: Замечание. Для нахождения интеграла следует разделить многочлен, стоящий в числителе, на знаменатель. Далее, произведя соответствующие преобразования (см. задачу 3), воспользоваться свойствами (4), (5) и формулой (2) (Т.И.). Решение.
Задача 6. Найти интеграл (выполнить по образцу задачи 5):
Задача 7. Найти интегралы: 1) 2) Указание. В первом интеграле числитель возвести в квадрат, полученный многочлен разделить на знаменатель и после этого проинтегрировать. Во втором интеграле открыть скобки, сделать преобразования, после чего выполнить интегрирование.
Задача 8. Найти интеграл: Решение. Иногда, с целью сведения подынтегральной функции к табличному интегралу, используют так называемый искусственный прием (прибавляют и вычитают одно и то же число в числителе с целью создания слагаемого, кратного знаменателю).
В данном случае в числителе прибавляют и вычитают 1.
Теперь проинтегрируем полученное выражение:
Задание для самостоятельной работы
Задача 9. Найти интегралы: 1) 2) 3) 4) 5) 6) 7) 8)
Задача 10. Найти интегралы: 1) 2) 3) Указание. Для решения примеров 1 и 2 использовать тригонометрические формулы:
Пример 3 решить по образцу задачи 8.
Задача 11. Найти интегралы: 1) 2) 3) 4) 5) 6) 7) Указание. Для решения примеров 5, 6, 7 используются формулы (12), (13), (14) (Т.И.).
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.227 (0.009 с.) |

 геометрически представляет множество интегральных кривых вида
геометрически представляет множество интегральных кривых вида  , отличающихся друг от друга постоянным слагаемым с (рис. 1).
, отличающихся друг от друга постоянным слагаемым с (рис. 1).
 ;
; ;
; ;
; ;
; ;
; .
. и т.д.
и т.д. ;
; .
. находится по формуле (2) (Таблицы интегралов - Т.И.) как интеграл степенной функции. Зная, что
находится по формуле (2) (Таблицы интегралов - Т.И.) как интеграл степенной функции. Зная, что 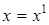 , т.е. в данном случае
, т.е. в данном случае 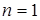 .
.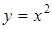 , где
, где  ;… (рис. 2).
;… (рис. 2). Рис. 2
Рис. 2
 ,
,

 ,
,



 ,
,

 ,
,
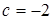

 .
. .
.
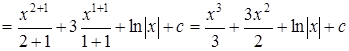 .
.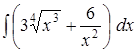 .
. , то данные интегралы находятся по формуле (2) (Т.И.) как интегралы от степенных функций. Прежде чем применить формулу (2), необходимо произвести преобразования подынтегральных функций. Для этого воспользуемся следующими свойствами:
, то данные интегралы находятся по формуле (2) (Т.И.) как интегралы от степенных функций. Прежде чем применить формулу (2), необходимо произвести преобразования подынтегральных функций. Для этого воспользуемся следующими свойствами: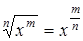





 .
. ;
; .
. .
.
 .
. .
. ;
;
 .
. .
. выражение не изменилось, но теперь можно преобразовать подынтегральную функцию:
выражение не изменилось, но теперь можно преобразовать подынтегральную функцию: .
. .
. ;
; ;
; ;
; ;
; ;
; ;
;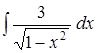 ;
;
 ;
; ;
; .
. .
. ;
; ;
; ;
; ;
; ;
;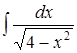 ;
;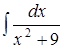 .
.


