
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №3. Несобственные интегралыСодержание книги
Поиск на нашем сайте
Цель занятия: усвоить правила вычисления несобственных интегралов на уровне знания и умения решать типовые задачи по теме.
Краткая информация о новых учебных элементах
1. Несобственные интегралы первого рода
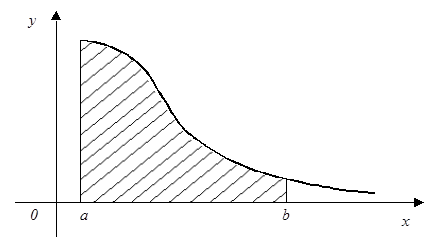
Несобственные интегралы с бесконечными пределами (или I рода) (рис. 2) определяются следующим образом:
Рис. 2
Несобственные интегралы I рода называются сходящимися, если существуют конечные пределы, стоящие в правых частях равенств (1). Если же указанные пределы не существуют или бесконечны, то несобственные интегралы называются расходящимися. Для установления сходимости интегралов (1) можно воспользоваться следующими признаками: 1. Если на промежутке 2. Если при 3. Если сходится интеграл
2. Несобственные интегралы второго рода
Если функция
Аналогично, если функция
Если функция
Рис.3
Если пределы, стоящие в правой части равенств (2), (3), (4) существуют, то несобственные интегралы II рода называются сходящимися; в противном случае – расходящимися. Для установления сходимости интегралов (2)-(4) можно воспользоваться следующими признаками: 1. Если на промежутке 2. Пусть функции 3. Если функция
Задача 1. Дан интеграл Решение. Предположим, что
Следовательно, если
т.е. данный интеграл сходится. Если
т.е. данный интеграл расходится. Если
т.е. данный интеграл расходится.
Задача 2. Исследовать сходимость несобственного интеграла Решение. По определению несобственного интеграла I рода
интеграл расходится, т.к.
Задача 3. Исследовать на сходимость интеграл Решение. Здесь
Поэтому, согласно признаку сравнения, интеграл
Задача 4. Вычислить несобственный интеграл Решение. Подынтегральная функция
Тогда имеем:
Интеграл сходится. Следовательно, исходный интеграл также сходится и равен
Задача 5. Найти значение несобственных интегралов или установить их расходимость (решить задачи по образцу):
2) 3) 4)
Задача 6. Вычислить несобственный интеграл Решение. Подынтегральная функция терпит бесконечный разрыв в точке
т.е. данный интеграл сходится.
Задача 7. Исследовать несобственный интеграл на сходимость
Решение. Подынтегральная функция терпит разрыв в точке
Так как несобственный интеграл
т.е. сходится, то сходится и исходный интеграл.
Задача 8. Исследовать несобственные интегралы на сходимость (по образцу задач 6,7): 1) 2) 3)
Задание для самостоятельной работы
Исследовать несобственные интегралы на сходимость: Задача 9.
Задача 10.
Задача 11.
Задача 12.
Задача 13.
Задача 14.
Занятие №4. Геометрическое приложение определенного интеграла
Цель занятия: закрепить правила вычисления определенных интегралов на уровне знания и умения решать типовые задачи по теме; уметь применять определенные интегралы к решению прикладных задач геометрии.
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 (1)
(1)
 непрерывные функции
непрерывные функции  и
и 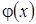 удовлетворяют условию
удовлетворяют условию  , то из сходимости интеграла
, то из сходимости интеграла  следует сходимость интеграла
следует сходимость интеграла  , а из расходимости интеграла
, а из расходимости интеграла  и существует конечный предел
и существует конечный предел  , то интегралы
, то интегралы 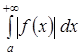 , то сходится и интеграл
, то сходится и интеграл 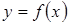 непрерывна в промежутке
непрерывна в промежутке  и имеет разрыв II-го рода при
и имеет разрыв II-го рода при 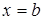 , то несобственный интеграл от неограниченной функции (II рода) определяется следующим образом:
, то несобственный интеграл от неограниченной функции (II рода) определяется следующим образом: . (2)
. (2) , то полагают
, то полагают . (3)
. (3)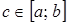 (рис. 3), то несобственный интеграл второго рода определяется формулой
(рис. 3), то несобственный интеграл второго рода определяется формулой . (4)
. (4)
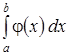 следует сходимость интеграла
следует сходимость интеграла  , а из расходимости интеграла
, а из расходимости интеграла  , то интегралы
, то интегралы  , имеет разрыв в точке
, имеет разрыв в точке  сходится, то сходится и интеграл
сходится, то сходится и интеграл  . Установить, при каких значениях
. Установить, при каких значениях  этот интеграл сходится, а при каких – расходится.
этот интеграл сходится, а при каких – расходится. . Тогда
. Тогда
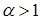 , то
, то ,
, , то
, то ,
, , то
, то ,
, .
.
 ,
, и
и 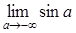 не существуют.
не существуют. .
. при
при  , при этом
, при этом  . Но интеграл
. Но интеграл  .
.
 определена и непрерывна на всей числовой оси. Эта функция является четной. Следовательно,
определена и непрерывна на всей числовой оси. Эта функция является четной. Следовательно, .
. .
. .
. ;
; ;
;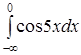 ;
; .
. .
.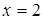 . Следовательно,
. Следовательно,
 ,
, .
. . Очевидно, что при
. Очевидно, что при 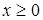
 .
.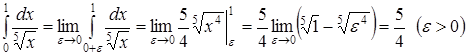 ,
, ;
; ;
; .
.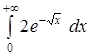 .
. .
. .
. .
. .
. .
.


