
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для решения кубического уравненияСодержание книги
Поиск на нашем сайте
а) рассмотрим делители свободного члена б) разделим многочлен
в) решим квадратное уравнение:
Значит, график пересекает ось Ох в точке 3. Промежутки знакопостоянства функции. Итак, многочлен, определяющий данную функцию можно разложить на множители:
Если Если Если Значит, на 4. Чётность. Вычислим
Значит, функция не обладает данными свойствами. 5. Исследование на экстремум.
Составим таблицу и определим знак производной в каждом интервале.
Найдем значения функции в точках экстремума.
Изобразим эти точки на графике.
Рис. 5 6. Исследование на перегиб.
Отметим эту точку Подставим координаты
значит, касательная имеет уравнение
7. Построение графика (рис. 5). Для уточнения положения графика найдем координаты некоторых его точек:
Задача 2. Исследовать функцию и построить ее график:
Решение. 1. Область определения функции. Делить на 0 нельзя, поэтому 2. Точки пересечения с осями. С осью Оу:
С осью Ох:
3. Промежутки знакопостоянства функции:
4. Исследование на экстремум.
Экстремума нет, т.к. критическая точка 5. Исследование на перегиб.
При переходе через точку
Рис. 6 6. Построение асимптот (наклонных):
Строим прямую по точкам:
7. Построение графика (рис. 6). Для уточнения положения графика найдем значение заданной функции в точках
Задача 3. Исследовать функцию и построить ее график:
1. Область определения – все действительные числа. 2. Точки пересечения с осями. С осью Оу: С осью Ох: 3. Промежутки знакопостоянства функции.
4. Исследование на экстремум.
5. Исследование на перегиб.
6. Построение асимптот.
Следовательно, ось Ох является горизонтальной асимптотой. 7. Для построения графика (рис. 7) вычислим значения функции в некоторых точках:
Рис. 7
Задание для самостоятельной работы
Задача 4. Исследовать функцию и построить ее график:
Задача 5. Исследовать функцию и построить ее график:
Задача 6. Исследовать функцию и построить ее график:
Исследовать функции и построить графики: Задача 7.
Задача 8.
Задача 9.
ТЕМА 3. КОМПЛЕКСНЫЕ ЧИСЛА
Цель занятия: изучение математического аппарата комплексных чисел, необходимого для глубокого усвоения общенаучных, общеинженерных дисциплин, решения прикладных задач с применением комплексных чисел, воспитания навыков самостоятельной деятельности, целеустремленности и трудолюбия в достижении поставленной цели.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.01 с.) |

 :
:  ; если
; если  , то
, то  , значит
, значит  корень данного уравнения.
корень данного уравнения. на двучлен
на двучлен  , т.е.
, т.е.  :
:
 .
. .
. . Определим знак функции в каждом из интервалов:
. Определим знак функции в каждом из интервалов: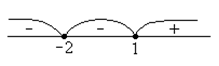
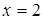 , то
, то  .
. , то
, то  .
. , то
, то  .
. график функции располагается ниже оси Ох, а на
график функции располагается ниже оси Ох, а на  - выше.
- выше. .
. и
и  .
. ;
; критические точки.
критические точки.





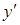








 ;
; .
.
 , если
, если  меняет знак, т.к.
меняет знак, т.к. 
 .
. на графике.
на графике. где
где  :
: ,
, . Построим ее:
. Построим ее:




 .
. ,
,  , значит
, значит  вертикальная асимптота.
вертикальная асимптота.
 ;
;
 .
.

 при
при 
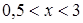
 при
при 
 .
.
 .
. , в которой
, в которой  , не входит в область определения.
, не входит в область определения.
 .
.
 .
.
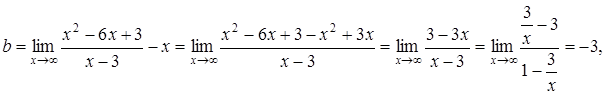
 .
. .
.







 .
.
 .
.
 ;
; .
. ;
; .
.



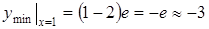 .
. .
. - точка перегиба, т.к.
- точка перегиба, т.к.  при всех х.
при всех х. при
при 
 при
при  .
. . Точка перегиба
. Точка перегиба 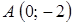 .
.
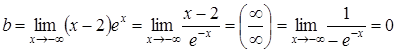 .
. ;
;  .
.
 .
. .
. (При построении графика масштаб: 1ед.
(При построении графика масштаб: 1ед.  3 клеткам).
3 клеткам). .
. .
. .
.


