
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №2. Метод замены переменныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель занятия: усвоить метод подстановки, закрепить знание таблицы основных интегралов.
Учебные вопросы
1. Дифференциал функции, его свойства (повторение). 2. Интегрирование с помощью подстановки.
Краткая информация о новых учебных элементах
Во многих случаях для вычисления интеграла требуется введение новой переменной интегрирования, которое позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т.е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной. Формула замены переменной имеет вид:
Задание для студентов
Задача 1. Решить устно (повторение). Найти дифференциал по формулам:
1. 2. 3.
Задача 2. Найти интегралы с помощью замены переменной.
Решение. Вспомним таблицу:
Следовательно, для того, чтобы найти интеграл от функции сложного аргумента, необходимо, чтобы подынтегральное выражение содержало производную аргумента. Поэтому данные интегралы в задаче 2 непосредственным интегрированием брать нельзя. Для решения данных интегралов используют замену: а) обозначить аргумент функции новой переменной и, где и – есть функция от х; б) найти в) из равенства (*) выразить dx; г) осуществить замену под знаком интеграла, сокращая в числителе и знаменателе функцию от х и вынося const за знак интеграла; д) полученный интеграл взять по таблице; е) вернуться к прежней переменной х.
Замечание. В данном примере целесообразнее выразить
Задача 3. Найти интегралы: 1) 2) 3) 4)
Задача 4. Найти интегралы: 1) 2) 3)
Задача 5. Найти интегралы: 1) 2) 3)
Задача 6. Найти интегралы: 1) 2)
Проанализируйте результаты интегрирования и дайте ответ на вопрос: чему равен Запомнить:
Т.е.
Задача 7. Найти интеграл методом подстановки: Решение.
Задача 8. По образцу задачи 7 найти интегралы: 1) 2) 3)
Задача 9. Решить методом подстановки: Решение.
Задача 10. Найти интегралы (по образцу задачи 9): 1) 2)
Проанализируйте задачи 9, 10 и сделайте вывод: при каких условиях интеграл, содержащий Задания для нахождения первообразной (устно)
Задание для самостоятельной работы
Задача 11. Найти интегралы: 1) 2) 3) 4) 5)
Задача 12. Найти интегралы: 1) 2) 3) 4) 5) 6) 7) 8) Занятие №3. Метод интегрирования по частям
Цель занятия: усвоить интегрирование по частям на уровне знаний и умений решать типовые задачи, закрепить метод интегрирования с помощью замены переменной.
Учебные вопросы
1. Замена переменной в неопределенном интеграле. 2. Интегрирование по частям.
Ход занятия
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.91 (0.01 с.) |

 .
.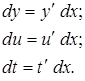
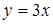 ;
; ;
; .
.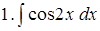 ;
;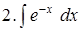 ;
;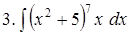 ;
; .
.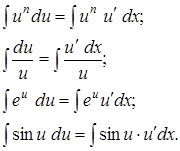
 ; (*)
; (*)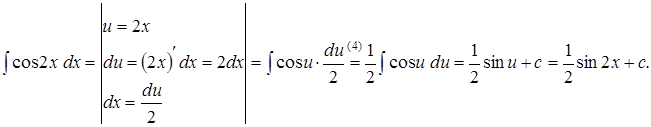
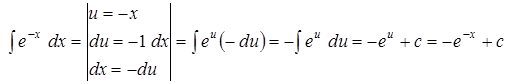 .
.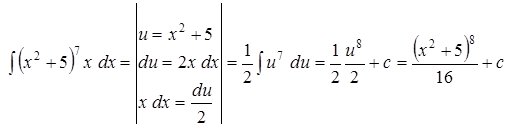 .
.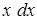 из
из 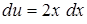 .
.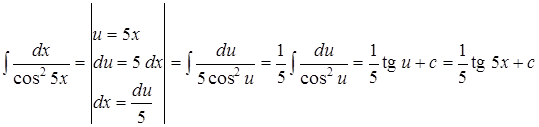 .
. ;
; ;
; ;
;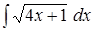 .
.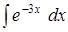 ;
; ;
;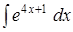 .
. ;
; ;
;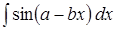 .
.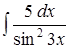 ;
;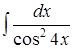 .
.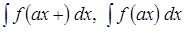 ?
?
 , где
, где 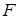 первообразная для функции f.
первообразная для функции f.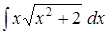 .
.
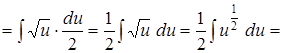
 .
.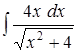 ;
; ;
;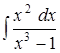 .
.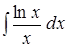 .
.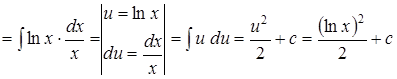 .
.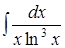 ;
;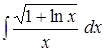 .
.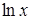 , является табличным?
, является табличным?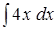 ;
;
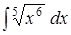 ;
;
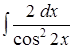 ;
;
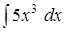 ;
;
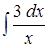 ;
;
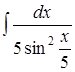 ;
;
 ;
;
 ;
;
 ;
;
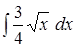 ;
;
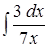 ;
;
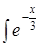
 ;
;
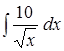 ;
;
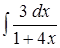 ;
;
 ;
;
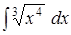 ;
;
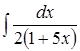 ;
;
 ;
;
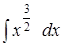 ;
;
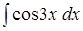 ;
;
 ;
;
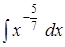 ;
;
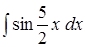 ;
;
 ;
;
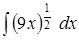 ;
;
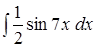 ;
;
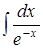 ;
;
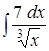 ;
;
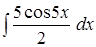 ;
;
 ;
;
 ;
;
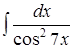 ;
;
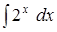 ;
;
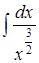 ;
;
 ;
;
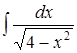 ;
;
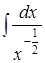 ;
;
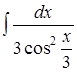 ;
;
 .
.
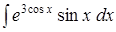 ;
; ;
; ;
; ;
;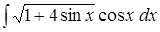 .
.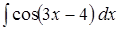 ;
;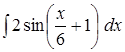 ;
; ;
;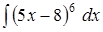 ;
; ;
; ;
;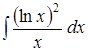 ;
;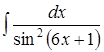 .
.


