
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм нахождения интеграла методом неопределенных коэффициентовСодержание книги
Поиск на нашем сайте
1) Проверить, правильная ли дробь. Если дробь неправильная, то необходимо представить её в виде суммы многочлена и правильной дроби. Это достигается делением числителя на знаменатель по правилу деления многочлена на многочлен. 2) Знаменатель правильной дроби разложим на простейшие множители вида 3) Правильную рациональную дробь разложим на простейшие дроби:
где 4) Для вычисления неопределенных коэффициентов приводим равенство (1) к общему знаменателю, приравнивая коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества, и решаем систему линейных уравнений относительно искомых коэффициентов. Тем самым интегрирование рациональной дроби сводим к интегрированию суммы простейших рациональных дробей.
Задача 1. Определить, правильная ли дробь:
Задача 2. Представить в виде суммы многочлена и правильной дроби неправильную дробь:
Решение. Дробь неправильная, т.к. степень числителя больше степени знаменателя. Разделим числитель на знаменатель по правилу деления многочленов.
Таким образом:
Задача 3. Найти интеграл: Решение. 1. Дробь правильная, т.к. степень числителя меньше степени знаменателя. 2. Разложим знаменатель на простейшие множители:
3. Представим подынтегральную функцию в виде суммы двух простейших дробей:
4. Найдем коэффициенты А и В. Для этого приведем дроби к общему знаменателю и воспользуемся правилом равенства дробей:
Приравниваем коэффициенты при х и свободные члены. Составим систему уравнений и найдем А и В:
Решив систему, получили
Тогда:
Задача 4. Найти интеграл: Решение. 1. Дробь правильная. Знаменатель разложен на множители. 2. Правильную рациональную дробь разложим на простейшие дроби по формуле (1):
3. Найдем коэффициенты А, В, С. Для этого приведем дроби к общему знаменателю:
По правилу равенства дробей:
Приведем подобные члены в правой части тождества:
Приравниваем коэффициенты при одинаковых степенях х и свободные члены в левой и правой части. Так как в левой части нет
Таким образом, решив систему, получим:
Тогда
Задача 5. Найти интеграл методом неопределенных коэффициентов:
Решение. 1. Дробь правильная. 2. Разложим знаменатель на множители:
3. Представим подынтегральную функцию в виде суммы двух простейших дробей:
4. Найдем коэффициенты А, В, С:
Приравниваем коэффициенты при
Таким образом:
Тогда
Задача 6. Найти интегралы методом неопределенных коэффициентов: 1) 2) 3) 4) 5) 6) 7) 8)
Задание для самостоятельной работы
Найти интегралы: Задача 7.
Задача 8.
Задача 9.
Задача 10. Указание. Подынтегральную функцию представить в виде суммы многочлена и правильной дроби (см. задачу 2). Правильную дробь разложить на множители, используя метод неопределенных коэффициентов, проинтегрировать.
Задача 11. Найти интеграл: Указание. а) знаменатель разложить на множители (разность кубов); б) используя метод неопределенных коэффициентов, получить два интеграла 1 и 3 типов; в) проинтегрировать по алгоритму.
Задача 12. Найти интеграл:
Найти интегралы, используя метод неопределенных коэффициентов: Задача 13.
Задача 14.
Задача 15.
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 2035; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.35 (0.005 с.) |

 и
и  .
.
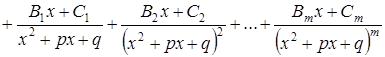 , (1)
, (1) неопределенные коэффициенты, которые нужно вычислить.
неопределенные коэффициенты, которые нужно вычислить.
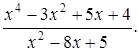

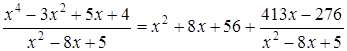 .
.
 .
.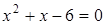 ;
; два действительных корня.
два действительных корня.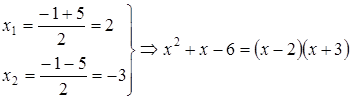 .
.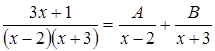 .
.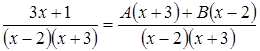 ;
;

 .
. . Таким образом:
. Таким образом: .
.
 .
. .
. .
. .
.
 .
. , то его коэффициент равен 0
, то его коэффициент равен 0 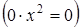 .
.
 .
. .
. ;
;
 .
. .
. .
. .
.
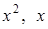 и свободные члены. Так как в левой части нет
и свободные члены. Так как в левой части нет  .
.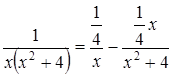 .
.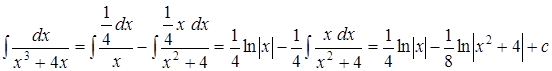 .
. ;
;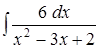 ;
; ;
; ;
; ;
; ;
; ;
; .
. .
.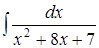 .
. .
. .
. .
. .
. .
. .
. .
.


