
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №1. Задачи, приводящие к понятию производнойСодержание книги
Поиск на нашем сайте
Цель занятия: усвоить новые учебные элементы на уровне знаний и умения применять при решении типовых задач.
Учебные вопросы 1. Решение задач физики, механики. 2. Решение задач геометрии.
Задача 1. Тело движется по прямой Ох по закону Решение. Согласно физическому смыслу производной, скорость
Задача 2. Решить задачу по образцу задачи 1. Точка движется по закону
Задача 3. Задача из курса «Теоретическая механика». Угол поворота диска, вращающегося вокруг неподвижной оси, изменяется согласно уравнению: Решение. Вращение диска согласно заданному уравнению происходит в одном и том же направлении. Поэтому можно считать
Имеем Таким образом Используя формулы угловой скорости
В момент времени
Задача 4. Написать уравнение касательной и нормали к параболе Решение. Уравнение касательной к графику Для составления этих уравнений необходимо знать: 1. координаты точки касания 2. угловой коэффициент касательной к данной кривой, который определяется по формуле: Итак, исходя из условия задачи, найдем координаты точки касания М
Найдем
Следовательно, уравнение касательной имеет вид:
Угловой коэффициент нормали будет
Тогда Построим данные линии (рис. 2). Задача 5. Решить задачу по образцу задачи 4. Написать уравнение касательной к кривой Задача 6. Под каким углом пересекаются кривые: Решение. Геометрическим образом уравнений Острый угол между касательными может быть вычислен по формуле:
где 1. Найдем
2. Найдем
Подставляя значения
Поскольку обе кривые симметричны оси Оу, то они в точках
Задание для самостоятельной работы
Задача 7. Составьте уравнение касательной и нормали к кривой
Задача 8. Под каким углом пересекаются кривые
Задача 9. Зависимость пути от времени при прямолинейном движении точки задана уравнением
Задача 10. По параболе
Задача 11. Написать уравнение касательных к гиперболе
Задача 12. Найти производные от функций: а) г)
|
||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.199 (0.006 с.) |

 . Определить скорость движения и ускорение.
. Определить скорость движения и ускорение. ; ускорение
; ускорение 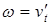 . Тогда
. Тогда  .
. .
. . Найти скорость и ускорение движения в момент времени
. Найти скорость и ускорение движения в момент времени  .
. (
( постоянная величина,
постоянная величина, 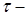 угол поворота тела в радианах,
угол поворота тела в радианах,  время в секундах). Определить ускорение (угловое) и угловую скорость диска через 4 сек. после начала движения, если за первые 2 сек. он сделал
время в секундах). Определить ускорение (угловое) и угловую скорость диска через 4 сек. после начала движения, если за первые 2 сек. он сделал 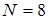 оборотов.
оборотов. , т.к.
, т.к.  и
и  .
. .
. .
.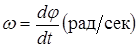 и углового ускорения
и углового ускорения  , получим:
, получим: .
. сек. имеем:
сек. имеем:
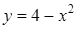 в точке пересечения ее с осью Ох (при
в точке пересечения ее с осью Ох (при  ) и построить параболу, касательную и нормаль.
) и построить параболу, касательную и нормаль. в т. М
в т. М  имеет вид
имеет вид  , а уравнение нормали
, а уравнение нормали  .
. .
.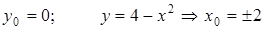 , получим
, получим .
. :
:  при
при  и
и при
при  .
. .
. .
.
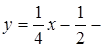 уравнение нормали, а также
уравнение нормали, а также 
 .
. в точке
в точке  . Построить касательную и кривую.
. Построить касательную и кривую. и
и  ?
? , решая которую, получим
, решая которую, получим 
 . Под углом пересечения двух кривых понимается острый угол, образованный касательными к соответствующим кривым в точке их пересечения.
. Под углом пересечения двух кривых понимается острый угол, образованный касательными к соответствующим кривым в точке их пересечения. , (1)
, (1)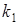 и
и  угловые коэффициенты касательных.
угловые коэффициенты касательных. угловой коэффициент касательной, проведенной к кривой
угловой коэффициент касательной, проведенной к кривой  :
: , т.е.
, т.е.  .
.
 :
: т.е.
т.е.  .
. в формулу (1), получим:
в формулу (1), получим: .
. пересекаются под равными углами.
пересекаются под равными углами.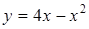 в точке
в точке  , определите угол, который образует касательная с положительным направлением оси Ох.
, определите угол, который образует касательная с положительным направлением оси Ох.
 ? Сделать чертеж.
? Сделать чертеж. (
( в метрах). Определить скорость движения в конце второй секунды.
в метрах). Определить скорость движения в конце второй секунды. движется точка так, что ее абсцисса изменяется в зависимости от времени t по закону
движется точка так, что ее абсцисса изменяется в зависимости от времени t по закону  (
( в метрах). Какова скорость изменения ординаты движения в точке
в метрах). Какова скорость изменения ординаты движения в точке  ?
? в точках
в точках 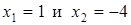 и найти угол между касательными. Построить кривую и касательные.
и найти угол между касательными. Построить кривую и касательные. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е) 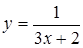 .
.


