
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №2. Производная сложной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель занятия: усвоить основные формулы таблицы производных на уровне знаний.
Учебные вопросы
1. Производная функции сложного аргумента.
Ход занятия Применяя формулы и правила дифференцирования, найти производные следующих функций: Задача 1. Решение. Заданная функция представляет собой многочлен. Применяя формулы (1, 2, 3, 6) из таблицы, найдем
Задача 2. Решение. Обозначим
Задача 3. Решение. Запишем данную функцию в виде
Задание для самостоятельной работы
Задача 4.
Задача 5.
Задача 6. Решение. Полагая
Задача 7.
Задача 8.
Задача 9.
Задача 10.
Задача 11.
Разобрать решение задач: Задача 12. Решение. Производную функций данного типа можно найти двумя способами: 1) применяем формулу
2) перепишем заданную функцию в виде:
Задача 13. Решение. Пользуемся формулой
Указание.
Задача 14. Решение. Воспользуемся формулой
Задача 15. Решить самостоятельно: Указание. Производную данной функции можно найти, пользуясь формулами
Найти производные от функций: Задача 16.
Задача 17.
Задача 18.
Задача 19.
Задача 20.
Задача 21.
Задача 22.
Задача 23.
Задача 24.
Задача 25.
Задача 26.
Задача 27.
Занятие №3. Производная сложной функции (продолжение)
Цель занятия: закрепить знание таблицы производных и умение применять ее формулы при решении типовых задач. Учебные вопросы
1. Производная сложной функции. 2. Вычисление производной функции в данной точке.
Ход занятия
Применяя формулы и правила дифференцирования, найдите производные следующих функций: Задача 1.
Задача 2. Решение. Обозначим
Задача 3.
Задача 4.
Задача 5. Решение. Обозначим
Задача 6. Решение. Обозначим
Задача 7.
Вычисление производной функции в данной точке
Задача 8. Решение. 1. Найдем производную заданной функции, пользуясь формулой
2. Для вычисления
Задача 9.
Задача 10. Решение. 1. Найдем
2.
Задача 11.
Задание для самостоятельной работы
Найти производные функций: Задача 12.
Задача 13.
Задача 14.
Задача 15.
Задача 16.
Задача 17.
Задача 18.
Задача 19.
Задача 20.
Задача 21.
Задача 22.
Задача 23.
Задача 24.
Задача 25.
Задача 26.
Задача 27. Дополнительная задача. Найти угол, под которым пересекаются параболы
Найти производные функций: Задача 28.
Задача 29.
Задача 30. Найти значения производной функции
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.249 (0.009 с.) |

 .
.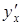 :
:

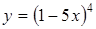 .
. , тогда
, тогда  . Применяя правило дифференцирования сложной функции и формулу
. Применяя правило дифференцирования сложной функции и формулу  , имеем:
, имеем:
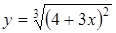 .
. . Обозначим:
. Обозначим: 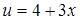 , тогда
, тогда  ,
,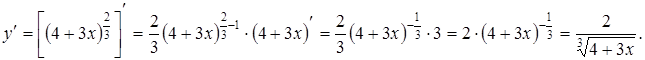
 .
. .
. .
. и применяя формулы (7, 9), будем иметь:
и применяя формулы (7, 9), будем иметь: .
.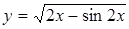 .
.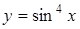 .
. .
.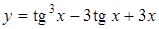 .
. .
. . Здесь роль v выполняет
. Здесь роль v выполняет  .
. .
. . Применяем формулу
. Применяем формулу  . Имеем:
. Имеем: .
. .
. . Обозначим
. Обозначим  ;
;  .
.
 .
. .
. .
. , где
, где  ,
,  , тогда
, тогда

 .
. .
. или
или  .
.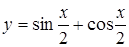 .
. .
. .
. .
. .
. .
.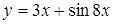 .
. .
. .
. .
.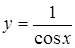 .
. .
. .
.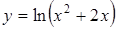 .
. , тогда
, тогда 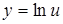 . Воспользуемся формулой
. Воспользуемся формулой 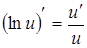 .
. .
.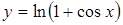 .
. .
. .
. , тогда
, тогда 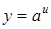 . Воспользуемся формулой
. Воспользуемся формулой 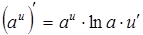 .
. .
. .
. , тогда
, тогда  . Воспользуемся формулой
. Воспользуемся формулой  .
. .
. .
.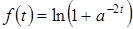 . Найти
. Найти  .
. . Обозначая
. Обозначая  , имеем
, имеем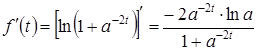 .
. переменной t дать значение 0, т.е. вычислить
переменной t дать значение 0, т.е. вычислить  .
.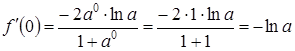 .
. . Найти
. Найти  .
. . Найти
. Найти  .
. . Обозначим
. Обозначим  , тогда
, тогда .
. .
. . Найти
. Найти  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. . Найти
. Найти  .
. и
и  .
. .
. .
. .
.


