
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие №2. Комплексные числа (продолжение)
Цель занятия: усвоить новые учебные элементы на уровне умения решать типовые задачи.
Учебные вопросы
1. Переход от алгебраической формы записи комплексного числа к показательной. 2. Действия над комплексными числами в показательной форме. 3. Применение комплексных чисел при решении различных задач.
Ход занятия
Задача 1. Представить в показательной форме комплексные числа:
Решение. Используем формулу (7) записи комплексного числа в показательной форме и формулы (8) перевода чисел из одной формы записи в другую. Из (7) следует, что нужно определить модуль комплексного числа 1) Так как
Таким образом, Аналогично определяется показательная форма записи для чисел 2) 3) 4) Задача 2. Представить в алгебраической форме комплексные числа:
Решение. Так как показательная и тригонометрическая формы записи используют одни и те же параметры 1)
По образцу задачи 2(1) получаем результаты во втором и третьем пунктах. Задача 3. Даны два комплексных числа Решение. Для выполнения действий над комплексными числами в показательной форме используем формулы (13-15): 1) 2) 3) Задача 4. Представив комплексные числа Указание. Задача решается по образцу задач 1, 3. Задача 5. Комплексное напряжение и ток пассивного двухполюсника равны: Решение. Запишем комплексное напряжение и ток в показательной форме:
Комплексное сопротивление определяем по формуле:
Задание для самостоятельной работы
Задача 6. Представив комплексные числа
Задача 7. Представить комплексные числа
Задача 8. Следующие комплексные числа
ТЕМА 4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Введение
В теме «Неопределенный интеграл» рассматривается задача, обратная задаче о дифференцировании функций. Задача состоит в следующем: дана функция К такой математической задаче приводят многие физические, химические и другие задачи, например, задача об отыскании закона равномерного движения материальной точки вдоль прямой по заданной скорости, задача о нахождении закона химической реакции по известной её скорости. Особое значение эта тема имеет при решении дифференциальных уравнений, описывающих различные физические и механические процессы. Для успешного усвоения навыков интегрирования надо, прежде всего, выучить наизусть таблицу интегралов и свойства интегралов.
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.187.121 (0.008 с.) |

 и аргумент комплексного числа
и аргумент комплексного числа  .
. , то
, то  , значит
, значит , т.к.
, т.к.  .
. .
. :
: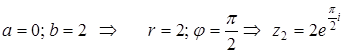 .
.
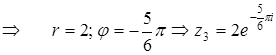 .
. .
. .
. , то, зная показательную форму, легко представить тригонометрическую форму комплексного числа, затем, вычислив значения тригонометрических функций, получаем алгебраическую форму.
, то, зная показательную форму, легко представить тригонометрическую форму комплексного числа, затем, вычислив значения тригонометрических функций, получаем алгебраическую форму. или по формулам (8):
или по формулам (8): ;
; .
.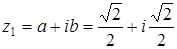 .
. . Вычислить: 1)
. Вычислить: 1)  .
. ;
;
 .
. в показательной форме, вычислить:
в показательной форме, вычислить:  .
. вольт и
вольт и  ампер. Вычислить комплексное сопротивление
ампер. Вычислить комплексное сопротивление  .
.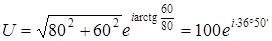 (вольт);
(вольт); (ампер).
(ампер). ,
,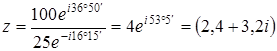 (ом).
(ом). ;
;  в показательной форме, выполнить действия: 1)
в показательной форме, выполнить действия: 1)  .
.
 в алгебраической форме записи.
в алгебраической форме записи. изобразить на комплексной плоскости, записать в тригонометрической и показательной формах. Выполнить действия над числами в показательной форме:
изобразить на комплексной плоскости, записать в тригонометрической и показательной формах. Выполнить действия над числами в показательной форме:  .
. , являющаяся производной некоторой функции
, являющаяся производной некоторой функции  ; требуется найти функцию
; требуется найти функцию 


