
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление значений сложной функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введение Предлагаемое пособие охватывает начальный курс математического анализа. В пособии излагаются определения основных учебных элементов, свойства пределов, производной, интеграла (определенного и неопределенного) функции одной переменной, а также их геометрический и физический смысл. Предполагается, что более глубокое изучение рассматриваемых тем студенты проводят по лекциям и по учебным пособиям самостоятельно. В пособии разобраны решения большого количества примеров, что позволит студентам самостоятельно провести анализ и выполнение остальных задач. Данное пособие предназначено для студентов технических специальностей и преподавателей, ведущих практические занятия у студентов технических специальностей. ТЕМА 1. ВВЕДЕНИЕ В АНАЛИЗ
Занятие №1. Пределы
Цель занятия: усвоить учебные элементы на уровне знаний. Закрепить навыки вычисления значения функции в точке, а также навыки вычисления пределов. Учитывая, что учебные элементы этого занятия знакомы студентам из средней школы, уделить особое внимание структуре сложной функции.
Краткие сведения из теории
Определение 1. Функция у от х, заданная цепью равенств
Определение 2. Говорят, что
Определение 3. Если
ТЕОРЕМА 1. (первый замечательный предел):
Основные эквивалентности при
1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Задание для студентов
Исходя из этих формул, приближенно вычислить:
Сравнить полученные значения с табличными данными.
Задание. Даны функции:
Вычислить:
Основные теоремы о пределах
ТЕОРЕМА 2. Если предел функции существует при
ТЕОРЕМА 3.
ТЕОРЕМА 4.
Следствие 1.
Следствие 2.
ТЕОРЕМА 5.
1. Раскрытие неопределенности вида
Для решения задач данного типа надо числитель и знаменатель дроби разделить на степень с наибольшим показателем в знаменателе.
Задача 1. Делим числитель и знаменатель на степень Применяя теорему о пределе частного (она применима, так как предел знаменателя равен 1, т.е. отличен от 0), получаем окончательный ответ.
Задача 2. Вычислить:
Задача 3. Вычислить:
Решить самостоятельно (вычислить пределы): Задача 4. Задача 5. Задача 6. Задача 7. Задача 8. 2. Раскрытие неопределенности вида
Задача 9. Вычислим корни трехчлена
Сократим дробь и вычислим предел, подставляя вместо х число 2.
Задача 10. Решается аналогично. Вычислить:
Задача 11. Вычислить Заменим
Задача 12.
Задача 13.
Задача 14.
Задача 15.
Ход занятия Применяя формулы и правила дифференцирования, найти производные следующих функций: Задача 1. Решение. Заданная функция представляет собой многочлен. Применяя формулы (1, 2, 3, 6) из таблицы, найдем
Задача 2. Решение. Обозначим
Задача 3. Решение. Запишем данную функцию в виде
Задание для самостоятельной работы
Задача 4.
Задача 5.
Задача 6. Решение. Полагая
Задача 7.
Задача 8.
Задача 9.
Задача 10.
Задача 11.
Разобрать решение задач: Задача 12. Решение. Производную функций данного типа можно найти двумя способами: 1) применяем формулу
2) перепишем заданную функцию в виде:
Задача 13. Решение. Пользуемся формулой
Указание.
Задача 14. Решение. Воспользуемся формулой
Задача 15. Решить самостоятельно: Указание. Производную данной функции можно найти, пользуясь формулами
Найти производные от функций: Задача 16.
Задача 17.
Задача 18.
Задача 19.
Задача 20.
Задача 21.
Задача 22.
Задача 23.
Задача 24.
Задача 25.
Задача 26.
Задача 27.
Ход занятия
Применяя формулы и правила дифференцирования, найдите производные следующих функций: Задача 1.
Задача 2. Решение. Обозначим
Задача 3.
Задача 4.
Задача 5. Решение. Обозначим
Задача 6. Решение. Обозначим
Задача 7.
Занятие №6. Подготовка к контрольной работе по теме 2
Цель занятия: закрепить знание учебных элементов и навыки решения типовых задач по теме.
Учебные вопросы
1. Производная сложной функции. 2. Производная функции, заданной параметрически. 3. Вычисление значений производной в точке. 4. Дифференциал функции. 5. Геометрические и механические приложения производной.
Пользуясь таблицей производных и правилом дифференцирования сложной функции, найти производные функций, разобрать решения следующих задач: Задача 1. Решение. Воспользуемся формулой
Задача 2. Решение.
Задача 3. Задача 4.
Задача 5. Разобрать решение задачи: Решение. Полагая Воспользуемся формулой
Задача 6. Решить самостоятельно:
Задача 7. Разобрать решение задачи: Решение. Воспользуемся формулой
Задача 8. Решить самостоятельно:
Задача 9. Разобрать решение задачи. Найти Решение. Так как
Имеем:
Задача 10. Решить самостоятельно: Задача 11. Разобрать решение задачи: Решение. Найдем:
Задача 12. Решить самостоятельно:
Задача 13. Разобрать решение задачи. Найти Решение. Воспользуемся формулой дифференциала функции
где
Решить самостоятельно: Задача 14. Найти
Задача 15. Найти
Задача 16. Закон движения точки по прямой задан формулой:
Определить скорость движения в конце второй минуты.
Задача 17. Составить уравнения касательной и нормали к кривой Решение. Найдем
Тогда уравнение касательной Уравнение нормали имеет вид:
Задание для самостоятельной работы
Найти производные от функций: Задача 18.
Задача 19.
Задача 20.
Задача 21.
Задача 22.
Задача 23.
Задача 24.
Задача 25.
Найти дифференциалы функций: Задача 26.
Задача 27.
Задача 28.
Задача 29. Найти
Задача 30. Найти
Задача 31. Найти
Задача 32.
Найти производные функций: Задача 33.
Задача 34.
Задача 35.
Задача 36.
Задача 37. Какой угол образует с осью Ох касательная к кривой
ТЕМА 3. КОМПЛЕКСНЫЕ ЧИСЛА
Цель занятия: изучение математического аппарата комплексных чисел, необходимого для глубокого усвоения общенаучных, общеинженерных дисциплин, решения прикладных задач с применением комплексных чисел, воспитания навыков самостоятельной деятельности, целеустремленности и трудолюбия в достижении поставленной цели.
Введение
В теме «Неопределенный интеграл» рассматривается задача, обратная задаче о дифференцировании функций. Задача состоит в следующем: дана функция К такой математической задаче приводят многие физические, химические и другие задачи, например, задача об отыскании закона равномерного движения материальной точки вдоль прямой по заданной скорости, задача о нахождении закона химической реакции по известной её скорости. Особое значение эта тема имеет при решении дифференциальных уравнений, описывающих различные физические и механические процессы. Для успешного усвоения навыков интегрирования надо, прежде всего, выучить наизусть таблицу интегралов и свойства интегралов.
ТАБЛИЦА ИНТЕГРАЛОВ
В этой таблице использовано свойство инвариантности формы полного дифференциала
При использовании формул этой таблицы для преобразования подынтегрального выражения к виду 1. 2. 3. 4. 5. 6. 7. Например,
Используя преобразования дифференциала можно дополнить свойства неопределенного интеграла: Если б) в)
Ход занятия
Ход занятия
Задача 3.
Задача 4.
Задача 5.
Задача 6. Выбрать метод интегрирования и найти интегралы: 1) 2) 3) 4) 5) 6) Задача 7. Найти интеграл:
Задача 8. Найти интеграл:
Задача 9. Найти интеграл:
Занятие №10. Подготовка к контрольной работе
Цель занятия: закрепить знания и умения, полученные при изучении темы «Неопределенный интеграл».
Учебные вопросы
1. Метод интегрирования: а) по частям; б) замена переменной; в) метод неопределенных коэффициентов; г) табличное интегрирование.
Ход занятия Задания для студентов на занятии и для самостоятельной работы
Задача 1. Выбрать метод интегрирования и найти интегралы:
Краткие сведения из теории
Пусть функция
Определение 1. Сумма вида
называется п-й интегральной суммой функции
Рис. 1
Геометрически сумма
Определение 2. Определенным интегралом от функции
где
а и b – соответственно нижним и верхним пределами интегрирования, х – переменной интегрирования.
ТЕОРЕМА 1. Если функция
ТЕОРЕМА 2. Если функция
Краткие сведения из теории
Пусть функция
При использовании этой формулы необходимо помнить: 1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется; 2) часто вместо подстановки 3) не следует забывать менять пределы интегрирования при замене переменных.
Если функции
Задача 1. Вычислить: Решение. Сделаем замену переменной по формуле
Задача 2. Вычислить: Решение. Положим
Решить задачи по образцу: Задача 3.
Задача 4.
При помощи формулы интегрирования по частям вычислить интегралы: Задача 5. а) Решение. а)
б)
Решить задачи по образцу: Задача 6.
Задача 7.
Задание для самостоятельной работы
Вычислить следующие интегралы: Задача 8.
Задача 9. Задача 10.
Задача 11.
Задача 12.
Задача 13.
Задача 14.
Задача 15.
Задача 16.
Рис.3
Если пределы, стоящие в правой части равенств (2), (3), (4) существуют, то несобственные интегралы II рода называются сходящимися; в противном случае – расходящимися. Для установления сходимости интегралов (2)-(4) можно воспользоваться следующими признаками: 1. Если на промежутке | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 , где
, где  , называется сложной или функцией от функции.
, называется сложной или функцией от функции. , если для любого
, если для любого 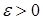

 такое, что
такое, что  при
при 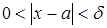 .
. , то функция
, то функция  называется бесконечно малой при
называется бесконечно малой при  . Заметим, что если
. Заметим, что если  - бесконечно большая величина.
- бесконечно большая величина. .
.
 где п и
где п и  натуральные;
натуральные; ;
; ;
; ;
; , где
, где  ;
;




 .
. .
.
 ;
; .
. , то он единственный.
, то он единственный. .
. .
. .
. .
. .
.
 .
. . Величины
. Величины  и
и  являются бесконечно малыми при
являются бесконечно малыми при  , поэтому
, поэтому  и
и  .
. .
. .
. .
. .
. .
. .
. .
.
 .
. :
: 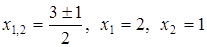 и разложим его на множители по формуле:
и разложим его на множители по формуле: ;
; .
. .
. .
. , тогда
, тогда  и
и 
 .
. .
. .
. .
. .
. .
.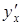 :
:

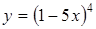 .
. , тогда
, тогда  . Применяя правило дифференцирования сложной функции и формулу
. Применяя правило дифференцирования сложной функции и формулу  , имеем:
, имеем:
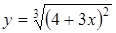 .
. . Обозначим:
. Обозначим: 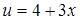 , тогда
, тогда  ,
,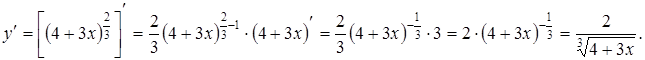
 .
. .
. .
. и применяя формулы (7, 9), будем иметь:
и применяя формулы (7, 9), будем иметь: .
.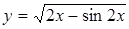 .
.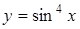 .
. .
.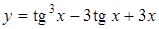 .
. .
. . Здесь роль v выполняет
. Здесь роль v выполняет  .
. .
. . Применяем формулу
. Применяем формулу  . Имеем:
. Имеем: .
. .
. . Обозначим
. Обозначим  ;
;  .
.
 .
. .
. .
. , где
, где  ,
,  , тогда
, тогда

 .
. .
. или
или  .
.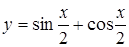 .
. .
. .
. .
. .
. .
.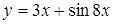 .
. .
. .
. .
.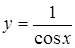 .
. .
. .
.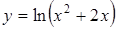 .
. , тогда
, тогда 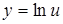 . Воспользуемся формулой
. Воспользуемся формулой 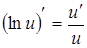 .
. .
.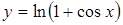 .
. .
. .
. , тогда
, тогда 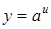 . Воспользуемся формулой
. Воспользуемся формулой 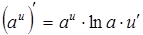 .
. .
. .
. , тогда
, тогда  . Воспользуемся формулой
. Воспользуемся формулой  .
. .
. .
. .
. , полагая
, полагая  ,
,  . Имеем:
. Имеем:
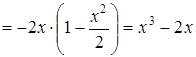 .
. .
.
 .
. .
. .
. .
.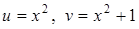 имеем
имеем  .
. :
:
 .
. .
. .
.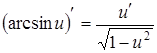 , полагая
, полагая  . Имеем:
. Имеем: .
. .
. , если
, если  .
. , найдем
, найдем .
. .
. . Найти
. Найти  . Найти
. Найти  .
. .
. .
. . Найти
. Найти  .
. .
. ,
, .
. .
.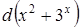 .
. .
. .
. в точке
в точке  .
. , следовательно, угловой коэффициент касательной будет:
, следовательно, угловой коэффициент касательной будет: .
. или
или  .
.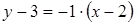 или
или  .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. , если
, если  .
. . Найти
. Найти  .
. .
. .
. .
. . Найти
. Найти  , проведенной в точке с абсциссой
, проведенной в точке с абсциссой  ?
? , являющаяся производной некоторой функции
, являющаяся производной некоторой функции  ; требуется найти функцию
; требуется найти функцию  , откуда
, откуда .
.
 при
при 







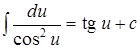









 применяются простейшие преобразования дифференциалов:
применяются простейшие преобразования дифференциалов: ;
; ;
; ;
; ;
; ;
; ;
; .
. .
. то а)
то а)  ;
; ;
; .
.





 ;
; ;
; ;
; ;
; ;
; .
. .
. .
. .
. ;
;
 ;
;
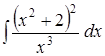 ;
;
 ;
;
 ;
;
 ;
;
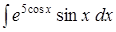 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
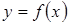 определена на отрезке
определена на отрезке  . Разобьем произвольным образом этот отрезок точками
. Разобьем произвольным образом этот отрезок точками  на п частичных отрезов длиной
на п частичных отрезов длиной  . Выберем в каждом из них точку
. Выберем в каждом из них точку 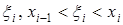 (рис. 1).
(рис. 1).

 представляет собой алгебраическую сумму площадей прямоугольников, заштрихованных на рис. 1, в основании которых лежат частичные отрезки
представляет собой алгебраическую сумму площадей прямоугольников, заштрихованных на рис. 1, в основании которых лежат частичные отрезки  , а высоты равны
, а высоты равны  .
. , т.е. по определению
, т.е. по определению , (1)
, (1) называется подынтегральной функцией,
называется подынтегральной функцией, подынтегральным выражением,
подынтегральным выражением, отрезком интегрирования,
отрезком интегрирования, , то она интегрируема на
, то она интегрируема на  .
. непрерывна вместе со своей производной и монотонна на отрезке
непрерывна вместе со своей производной и монотонна на отрезке  ,
,  и сложная функция
и сложная функция  непрерывна на
непрерывна на  . (1)
. (1) ;
; и
и  имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке  . (2)
. (2) .
. . Тогда
. Тогда  ,
, 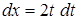 . При
. При  получим
получим  , а при
, а при  . Все перечисленные выше условия, при которых верна формула (1), выполнены. Следовательно,
. Все перечисленные выше условия, при которых верна формула (1), выполнены. Следовательно, .
. .
. . Тогда
. Тогда 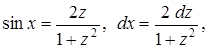
 . Следовательно,
. Следовательно,
 .
. .
. .
. ; б)
; б)  .
.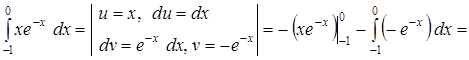
 .
.


 .
. .
. .
. .
. .
.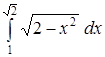 .
. .
. .
. .
. .
. .
. .
. непрерывные функции
непрерывные функции 


