Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальная сеть геофизических наблюдений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оптимальной сетью геофизических наблюдений называют сеть, которая с заданной вероятностью обеспечивает решение поставленной геологической задачи при относительно малых затратах средств. Если размеры аномалии, снятые по величине эллипса (а× в), где а и в большая и малая оси эллипса, определенные на уровне минимальной амплитуды аномалии Задача Бюффона заключается в определении вероятности р вероятности пересечения наугад бросаемой иглой длиной 2 l одной из параллельных линий, отстоящих на расстояние 2 d друг от друга. Бюффон показал, что
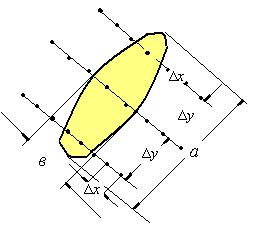
Например, при 2 l = 2 d вероятность обнаружения равна р = 0,636. В плане аномальные значения на уровне А мин можно аппроксимировать эллипсами с большой осью а и малой осью в. Коэффициенты сжатия эллипсов с = в/а могут быть: 0,7<с<1.0 – для изометрических тел, 0,3<с<0,7 – для линзообразных тел и 0,1<с<0,2 – для жил и пластов. На рис. 2.9.1 приведена сеть геофизических наблюдений Задача Бюффона была использована И. Д. Савинским для расчета таблиц вероятностей пересечений (а× в) - эллиптических объектов прямоугольной сетью наблюдений (Δ y ×Δ x).
Рис. 2.9.1. Сеть геофизических наблюдений
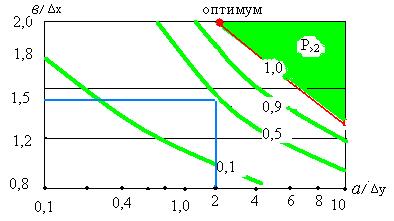
Вид номограммы И. Д. Савинского для определения вероятности подсечения эллиптических объектов не менее чем двумя точками при угле встречи эллипса с профилями наблюдений более 60о приведен на рис. 2.9.2.
Рис. 2.9.2. Номограмма для определения вероятности подсечения эллиптических объектов не менее чем двумя точками Р ›2 при угле встречи эллипса с профилями наблюдений более 60о.
Использование номограммы И. Д. Савинского для расчета оптимальной сети выявления объекта с вероятностью Р ›2. Пусть Р ›2 ≥ 0,95, в = 20 м., а = 100 м. Тогда в /Δ x = 2, а/ Δ y =2. Расчетная сеть Δ x = 10 м., Δ y = 50 м. Вероятности Р ›2 ≥ 0,95 соответствует также точка в /Δ x = 1,5, а/ Δ y =10. В этом случае расчетная сеть будет Δ x = 14 м., Δ y = 10 м. Однако такая сеть будет в пять раз дороже, чем в первом варианте расчета, так как количество профилей наблюдений увеличивается в пять раз по сравнению с первым вариантом расчета. Поэтому такая сеть не оптимальна по стоимости. Для выбора оптимального варианта сети следует выбирать левую верхнюю точку эквивалентных вероятностей по номограмме И. Д. Савинского. Номограммы И. Д. Савинского можно использовать для определения вероятности обнаружения объекта. Например, если (а× в) = (400×30 м.), а сеть наблюдений (Δ y ×Δ x) = (200×20 м.), то вероятность обнаружения такого объекта будет равна Р ›2 = 0,5, так как по номограмме И. Д. Савинского в /Δ x = 1,5, а/ Δ y =2. В наземной геофизике применяются: - площадная квадратная съемка (изометрические аномалии), - площадная прямоугольная съемка (вытянутые аномалии), - площадная маршрутная съемка (мелкомасштабная по сети дорог), - профильная съемка (рекогносцировочная и интерпретационные маршруты) - специальные виды съемки (радиальная, спиральная и т. д.) Критерием для выбора сети являются: интенсивность и вид (форма) аномалии. Если критерием является интенсивность аномалии, то определяются размеры аномалии, снятые по величине эллипса (а× в), где а и в большая и малая оси эллипса, определенные на уровне минимальной амплитуды аномалии Если критерием является форма аномалии, то густота сети увеличивается так, чтобы можно было обнаружить не только максимальный, но и минимальный экстремум аномалии. Точность выбора густоты сети определяется точностью привязки сети на местности, равной точности нанесения точки на план (1 мм.). Густота выбора профилей на местности равна масштабу съёмки и равна 1 см. на плане.
|
||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 976; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.174.253 (0.01 с.) |

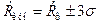 , то в качестве оптимальной берется сеть (0,9 а ×0,9 в). В общем случае вероятность пересечения объекта сетью наблюдений определяется путем решения задачи Бюффона.
, то в качестве оптимальной берется сеть (0,9 а ×0,9 в). В общем случае вероятность пересечения объекта сетью наблюдений определяется путем решения задачи Бюффона.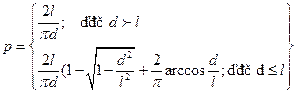
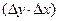 , пересекающая эллипс (а× в)-аномалии пятью точками наблюдений.
, пересекающая эллипс (а× в)-аномалии пятью точками наблюдений.