Нормальное геофизическое поле, аномалия, помеха

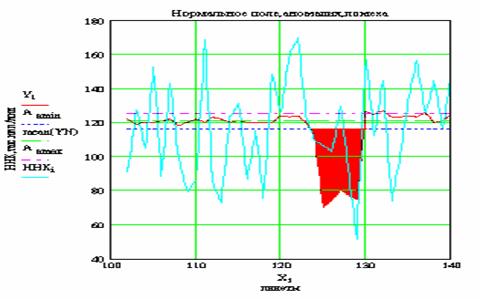
При геологическом истолковании геофизических данных большое значение имеют понятия нормального геофизического поля, аномалии и помехи. Под геофизической аномалией понимается отклонение физического поля от его нормальных значений. Нормальным полем считается геофизическое поле, обусловленное однородными по физическому параметру горными породами.

Нормальное поле может быть искусственным и естественным. Нормальное искусственное поле определяется полем заданного источника в однородной бесконечной среде. Нормальное естественное поле задается полем Земли.

В частности нормальное поле силы тяжести g ₀ вычисляется по Ф. Гелъмерту: , где g _экв - значение силы тяжести на экваторе, j - широта местности, β₁, β₂ - константы по Ф. Гелъмерту.

Аномалией считается уклонение измеренного значения поля g от нормального поля силы тяжести Δ g = g - g ₀ с поправкой за высоту точки наблюдения (аномалия Фая) и за промежуточный слой (аномалия Буге).

Нормальное магнитное поле Т ₀ является суммарным магнитным полем ди­поля Земли Т _Д, материков Т _М и космического пространства Т _К: Т ₀ = Т _Д + Т _М + Т _К. Аномалией считается уклонение измеренного магнитного поля Т от нормального магнитного поля Δ Т = Т – Т ₀. В настоящее время составлены подроб­ные карты нормального магнитного поля (изодинамы) и градиента нормального поля (изопоры) для всей территории России.

При выделении аномалий действует принцип относительности. От крупных и мелких структурных единиц выделяются аномалии различных порядков. Поэтому часто используют понятие местного нормального поля, под которым понимают относительно спокойное поле, типичное в среднем для участка геофизической съёмки.

При выделении локальных и региональных аномалий следует помнить, что локальная аномалия по своим линейным размерам в пять раз меньше изучаемой площади (профиля). Региональная аномалия по линейным размерам в пять раз и более превышает размер локальных аномалий.

Для выделения аномалий на фоне помех используются статистические критерии. Аномальными считаются точки, на которых амплитуда измеренного поля превышает уровень разрешенной изменчивости нормального поля. Уровень изменчивости характеризуется величиной общей дисперсии наблюденного поля D ₀, которая складывается из природной дисперсии D _г, определяемой геологическими факторами и дисперсии геофизической съемки D _c,определяемой точностью измерений, D ₀ = D _г+ D _c.

Аномалии делятся на региональные и локальные. В качестве модели поля принимается аддитивная модель, т. е. результаты измерений в i -й точке f_{i .} имеют вид: f_i = a_{i рег}+ a_iлок+n_iпом, где a_iрег – региональная (фоновая) составляющая аномалии, a _iлок – локальная аномалия, n _iпом – помеха.

При разделении полей на региональную и локальную составляющие модель поля упрощается. При выделении региональной составляющей локальную составляющую относят к помехам, а при выделении локальной составляющей региональную составляющую относят к помехам.

Для выделения аномалий на фоне помех используются статистические критерии. Аномальными считаются точки, на которых амплитуда измеренного поля превышает уровень разрешенной изменчивости нормального поля. Уровень изменчивости характеризуется величиной общей дисперсии наблюденного поля D ₀ = D _г+ D _c. По определению D = σ², где σ – среднеквадратическое отклонение случайной величины от ее математического ожидания. Поэтому вместо дисперсий можно записать σ₀² = σ_г² + σ_с², где σ₀ – общее среднеквадратическое отклонение наблюденного поля (стандарт), σ_г – среднеквадратическая погрешность геологических помех, σ_с – среднеквадратическая погрешность съемки.

Если фоновые значения поля распределены по нормальному закону, нижний аномальный предел А_мин, ограничивающий уровень разрешенных колебаний нормального поля, определяется соотношением А_мин = А_ф+3σ₀, где А_ф – среднее арифметическое частных значений нормального фона, σ₀ – общий стандарт наблюденного поля.

Если фоновые значения поля подчинены логнормальному закону, нижний аномальный предел, ограничивающий уровень разрешенных колебаний нормального поля, определяется из соотношения А_мин = А_фε³, где А_ф – среднее геометрическое частных значений нормального поля, ε – стандартный множитель. Фоновые значения могут превышать предел А_мин. Однако вероятность этого равна 0,0028, а вероятность закономерной эволюции 0,9972.

Требования к уровню А_мин могут быть снижены в случае коррелируемости точек с повышенными значениями поля по m профилям или при наличии n высоких значений подряд по профилю. При этом А_мин = А_ф+3σ₀/√m (m < 9), если фоновые значения распределены по нормальному закону. Требование (m < 9) обусловлено тем, что вероятность того, что 9 пикетов подряд в области нормального поля будут превышать нижний аномальный предел, изчезающе мала. По теореме умножения вероятностей Р (А_ф > А_мин) = 6·10^-8, т. е. высокие помехи одного знака, как независимые события, маловероятны.

К помехам относят факторы, осложняющие измерения геофизического поля. Помехи делятся на геологические и не геологические (вариации естественных геофизических полей, блуждающие промышленные токи и др.). Кроме того, помехи бывают случайные, обусловленные большим количеством неконтролируемых факторов, действие каждого из которых незначительно, и не случайные (систематические погрешности наблюдений, вариации фоновых значений поля и др.). В отличие от фоновых и аномальных значений геофизического поля помехи обычно отличаются относительно малой амплитудой и высокой частотой своих флюктуаций.

Рассмотрим пример выделения аномальных значений геофизического поля на фоне его нормальных значений. Например, необходимо по данным ядернофизиче­ских измерений в скважине определить расположение залежи медноколчедан­ной руды путем выделения аномальных значений регистрируемого нейтрон­ного поля методом ННК-Т. Полевые измерения проведены на Восточно-Семе­новском месторождении медно-цинковых колчеданов методом ННК-Т.

Измерения нейтронного поля выполнены по тепловым нейтронам в ин­тегральном варианте. Нейтронное поле создавалось с помощью Р о- В е-источ­ника нейтронов мощностью 4·10⁷ нейтрон/с. Для регистрации нейтронов использовался детектор типа ЛДНМ.

Наличие цинка и кадмия в медных рудах месторождения приводит к тому, что рудные интервалы выделяются минимумами скорости счета теп­ловых нейтронов.

В соответствии с правилами выделения аномалий на фоне нормального поля требуется оценить структуру поля по данным ННК-Т, выделить местное нормальное поле, учитывая, что рудная залежь выделяется понижениями значения поля на диаграммах ННК-Т. Затем следует найти нижний аномальный предел для каротажа ННК-Т в нормальном поле. По вычисленным значениям нижнего аномального предела выделить аномалии нейтронного поля на диаграммах ННК-Т.

В результате измерений установлено, что нормальное поле соответствует пикетам 111-124 (рис. 2.18). Аномальным значениям соответствуют пикеты 125-130. Введем некоторые обозначения из редактора Mathcad. Результаты каротажа ННК-Т по точкам i в нормальном поле обозначим YN_i; среднее значение данных ННК в нормальном поле mеаn (YN) = 120.957; стандарт ННК в нормальном поле stdev (YN) = 1.517; минимальное значение ННК в нормальном поле min(YN) = 118; нижний аномальный предел A_amin = mean (YN) - 3 stdev (YN); верхний аномальный предел А _{a max}:= mean (YN) + 3 stdev (YN).

На рис. 2.18. приведены результаты каротажа ННК-Т в нормальном поле (YNi), тысяч имп. мин, средние значения данных каротажа в нормальном поле (mean YN), верхний А _{a max} и нижний А _{a min} аномальные пределы.

 

 

Рис. 2.18. Результаты каротажа ННК-Т в нормальном поле (YNi):

(mean YN) - средние значения данных каротажа в нормальном поле; верхний А _{a max} и нижний А _{a min} аномальные пределы.

 

На рис. 2.19. приведены результаты разделения нормального поля и аномальных значений (Yi) по данным каротажа ННК-Т с учетом помех статистического происхождения ННКi), тысяч имп. мин, средние значения данных каротажа в нормальном поле (mean YN), верхний А _amax и нижний А _amin аномальные пределы для нормального поля.

 

Рис. 2.19. Результаты разделения нормального поля и аномальных значений (Yi) по данным каротажа ННК-Т с учетом интенсивных помех статистического происхождения (ННКi).

Помехи отличаются от нормального поля и аномалий по частотной характеристике (высокочастотный спектр помех).

Из рис. 2.19. видно, что аномальные значения каротажа ННК-Т (Yi) выходят за пределы нижнего аномального предела нормального поля А _amin . Вероятность аномальных значений на интервале профиля пикеты 125-130 превышает три стандартных погрешности нормального поля. Фоновые значения могут превышать предел А_мин. Однако вероятность этого равна 0,0028, а вероятность закономерной эволюции 0,9972, т. е. близка к единице и мы имеем дело с достоверным событием. Таким образом, на указанном интервале профиля расположен меднорудный пласт с повышенным содержанием цинка и кадмия.

При планировании точности наблюдений следует руководствоваться следующими положениями. Наблюдения с неоправданно высокой точностью ведут к увеличению затрат средств и времени, а недостаточная точность приводит к пропуску объекта.

Точность геофизической съемки определяется уровнем помех. При интенсивных помехах повышение точности измерений приводит к увеличению затрат труда и времени, но не дает желаемого результата. Возрастает лишь фиктивная, кажущаяся, а не истинная точность.

Планирование точности наблюдений основано на трех параметрах: минимальной амплитуде аномалии, подлежащей обнаружению А мин, среднеквадратической погрешностью геофизической съемки σ_с и среднеквадратической погрешностью геологических помех σ_г.

Нижний аномальный предел определяется путем решения прямой задачи для заданной физико-геологической модели (ФГМ) объекта поисков при наиболее неблагоприятных условиях от минимальных промышленных рудных тел или из опыта предшествующих геофизических работ.

Среднеквадратическая погрешность съемки оценивается по результатам повторных наблюдений и подсчитывается по формуле:

где f _i^о и f _i^п – основной и повторный замеры, n - число парных измерений.

Повторные наблюдения выполняются в пределах нормальных или фоновых значений в количестве 3-5 % от числа основных замеров.

Среднеквадратическая погрешность геологических помех определяется из соотношения .

Общая среднеквадратическая погрешность наблюдений определяется по разности наблюденных значений f_i и фоновых f_ф по формуле

где f_ф – среднее арифметическое результатов измерений в нормальном поле, которое подсчитывается по формуле

Обычно точность наблюдений, методику работ и аппаратуру подбирают так, чтобы расчетная аномалия от заданной физико-геологической модели объекта поисков превышала нижний аномальный предел А > А _мин.

При выполнении геофизических работ возможны два случая, определяемые уровнем геологических помех.

Если уровень помех геологического происхождения мал σ_c² >> σ_г ², то разрешающая способность геофизической съемки σ_c определяется аппаратурой и методикой работ. В этом случае целесообразно применять высокоточную прецизионную аппаратуру. Например, высокоточная магниторазведка σ_c = 1 - 2 нТл позволяет разделять слабомагнитные бокситы на фоне немагнитных известняков.

Если дисперсия геологических помех велика σ_г ² >> σ_с ^2, то использовать прецизионную съемку не имеет смысла. Например, нецелесообразно применять высокоточную магниторазведку в горных районах из-за помех, связанных с рельефом местности.

В качестве примера рассмотрим результаты измерений в методе вызванных потенциалов. Путем измерений установлено, что σ_с ² = 0,12, общая дисперсия наблюдений σ_о ² = 1,3. При этом = 1,18, т. е. дисперсия геологических помех велика σ_г ² >> σ_с ² и повышение точности наблюдений нецелесообразно.

Для снижения дисперсии съемки σ_с ² и дисперсии геологических помех σ_г ² используются следующие приемы. Дисперсия съемки зависит от порога чувствительности прибора, количества измерений на точке n с последующим усреднением σ_с ² = σ_с ²/n, и мешающих факторов, таких как вариации поля во времени, нормальных градиентов поля на участке работ, установки и центровки прибора на точке и других. Поэтому снижение дисперсии съемки достигается с помощью более точной аппаратуры, методики работ и введения поправок за влияние мешающих факторов. Влияние каждого фактора оценивается отдельно при неизменности влияния остальных факторов.

Уменьшение дисперсии геологических помех достигается статистической обработкой исходных данных. Обычное осреднение в пределах окна из n точек позволяет уменьшить дисперсию геологических помех в n раз σ_г ² = σ_г ²/ n. Кроме того помехи могут коррелировать между собой и отличаться от аномалий по частотной характеристике (по спектру). Поэтому, помехи геологического происхождения можно уменьшить путем соответствующих приемов обработки исходных данных (корреляционный и спектральный анализ).

Чаще всего уменьшение дисперсии геологических помех достигается путем осреднения в пределах окна из n пикетов. На рис. 2.20. приведены результаты сглаживания помех геологического происхождения в нормальном поле при каротаже ННК-Т.

Результаты сглаживания геологических помех свидетельствуют о том, что стандартное отклонение нормального поля до сглаживания stdev(ННК) = 15,8 уменьшается после сглаживании в два раза до stdev(smuННК) = 7,18. В результате нижний и верхний аномальные пределы после сглаживания можно значительно уменьшить.

 

 

Рис. 2.4.3. Результаты сглаживания помех геологического происхождения в нормальном поле при каротаже ННК-Т

 

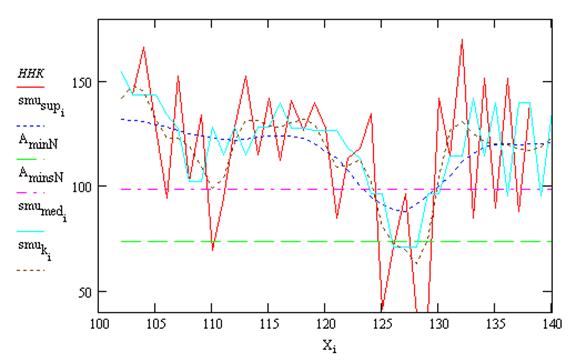
Теперь рассмотрим результаты каротажа ННК-Т с учетом аномальных значений и случайной высокочастотной помехи. Для этого введем обозначения, принятые в редакторе Mathcad: i = 1.. 40 – пикеты по оси скважины; dataННК – данные ННК; csort(dataННК) – сортировка данных ННК по возрастанию глубины; X: глубина скважины; У:= data(ННК) – данные ННК, тыс. имп/мин; ННК:= RND - mean(RND) + Y – данные ННК с погрешностью; mean(ННК) = 116.15 – среднее значение данных ННК; stdev(ННК) = 33.532 – стандарт ННК; smusup:= supsmooth (ННК) - данные ННК, линейно сглаженные методом наи­меньших квадратов; stdev(smusup) = 12.76 – стандарт данных ННК, линейно сглаженных методом наименьших квадратов; medsmooth(ННК) – данные ННК, сглаженные методом скользящей медианы; stdev (smumed) = 20.97 – стандарт данных ННК, сглаженных методом скользящей медианы; ksmooth(ННК) – данные ННК, сглаженные на основе распределения Гаусса; stdev (smuk) = 19.964 – стандарт данных ННК, сглаженных на основе распре­деления Гаусса; mean(smuННК) = 116.25 – среднее значение сглаженных дан­ных ННК.

Сглаживание высокочастотной помехи можно производить различными способами. На рис.2.21. приведены результаты различных видов сглаживания помех геологического происхождения при каротаже ННК-Т.

 

Рис.2.21. Результаты сглаживания помех геологического происхождения при каротаже ННК-Т, тыс. имп/мин:

smu.sup – данные ННК, линейно сглаженные методом наименьших квадратов; smu.med – данные ННК, сглаженные методом скользящей медианы; smu.k – данные ННК, сглаженные на основе распределения Гаусса

 

Результаты сглаживания геологических помех свидетельствуют о том, что стандартное отклонение нормального поля до сглаживания было stdev(ННК) = 33,5. После линейного сглаживания методом наименьших квадратов стандарт уменьшается до stdev(smu.sup) = 12,76. После линейного сглаживания мето­дом скользящей медианы стандарт уменьшается до stdev(smu.med) = 20,97. После линейного сглаживания на основе распределения Гаусса стандарт уменьшается до stdev(smu.k) = 19,9. Из перечисленных мето­дов сглаживания наилучшие результаты позволяет получить метод наимень­ших квадратов, который почти в два раза превосходит методы скользящей медианы и метод Гаусса.

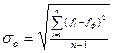
Среднеквадратическая погрешность съемки ННК-Т оцененная по результатам повторных наблюдений равна σ_с = 0.95. Общая среднеквадратическая погрешность наблюдений определенная по разности наблюденных значений f_i и фоновых f_ф равна σ_о = 6.42. Среднеквадратическая погрешность геологических помех σ_г = 6.35. Результаты расчетов свидетельствуют , т. е. дисперсия геологических помех превышает дисперсию съемки. В этом случае уменьшать дисперсию съемки не имеет смысла, так как в результате будет увеличиваться только точность выделения геологических помех. Уменьшение дисперсии геологических помех достигается статистической обработкой исходных данных, например, методом среднеквадратического сглаживания supsmooth (ННК).