
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка геологической эффективности геофизических методовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Геологическая эффективность геофизических методов на стадии поисковых работ оценивается по пиковому отношению сигнал-помеха. Аномалии разных методов сравниваются по контрастности. Под контрастностью аномалии понимают отношение превышения ее экстремума (Аmax, Amin) или (Аmax-Amin) для случая знакопеременных аномалий, над уровнем нормального фона Аф к величине среднеквадратической погрешности определения фона s: При стационарном и некоррелированном характере помех можно использовать отношение средних квадратов аномалии и помехи Геологическую эффективность геофизических методов можно оценить по надежности разделения объектов разных классов. Под надежностью разделения понимается вероятность правильного разделения. Если есть гипотезы H 1 и H 2, то ошибка первого рода α состоит в том, что при наличии гипотезы H 1 определяется гипотеза H 2. Ошибка второго рода β состоит в том, что при наличии гипотезы H 2 определяется гипотеза H 1. Вероятности ошибок α и β определяются площадями под плотностью распределения k -го признака x k. Если априорные вероятности классов H 1 и H 2 равны р 1 и р 2, то вероятность общей безусловной ошибки равна q = p 1 α + p 2 β, а вероятность правильного разделения при этом равна γ = 1- q. Обычно до опыта р 1 = р 2 = 0.5. Поэтому при полном совпадении гистограмм γ = 0.5, так как α + β = 1. В этом случае признак x k не обладает геологической эффективностью. Если же гистограммы объекта и помехи не пересекаются, то q = 0, γ = 1 и природа объектов H 1 и H 2 определяется однозначно. Таким образом, чем выше g, тем больше информативность. Пример надежности разделения геологических объектов разных классов приведен на рис. 2.11.1. Распределение плотности горных пород на базе геофизической практики УГГУ в поселке В. Сысерть подчиняется нормальному закону: для гранитов Построим гистограммы распределения плотности гранитов и гнейсов.
Рис 2.11.1.Оценка надежности разделения геологических объектов разных классов по плотности в поселке В. Сысерть Для оценки надежности разделения горных пород разных типов g можно использовать способ проверки статистических гипотез
Подсчитаем ошибки первого и второго рода.
a = 0,035, b = 0,224, a + b =0.26. При этом вероятность общей безусловной ошибки равна q = 0,5(a +b) = 0,13, а вероятность надежного разделения гранитов и гнейсов равна g = 1 – q = 0,87. Считается, что если g меньше, чем 0.75, то надежное разделение не возможно. Поэтому в рассматриваемом случае граниты и гнейсы можно разделить по данным гравитационной разведки. Для оценки геологической эффективности геофизических методов часто используют понятия теории вероятностей [6] и теории информации. Краткие сведения из теории вероятностей. В теории вероятностей под событием понимают факт, который в результате опыта может произойти или не произойти. Сформулируем основные положения теории вероятностей. Вероятностью события р называется число, которое тем больше, чем более возможно событие. Единицей измерения вероятности является вероятность достоверного события, которое в результате опыта должно произойти непременно. Событие, которое не может произойти, называется невозможным. Его вероятность равна нулю. Таким образом, 1 ≥ р ≥ 0. Суммой событий называется событие, состоящее в появлении хотя бы одного из этих событий. Произведением событий называется событие, состоящее в совместном появлении всех этих событий. События А1, А2,…Аn образуют полную группу событий, если в результате опыта непременно появится хотя бы одно из них, если они попарно несовместимы, а в сумме образуют достоверное событие. Несовместными событиями называются события, которые в данном опыте не могут появиться вместе. Случаем (шансом) называется одно из событий полной группы несовместных, равновозможных событий. Случай называется благоприятным некоторому событию, если появление этого случая влечет за собой появление данного события. Вероятность события А вычисляется как отношение числа благоприятных случаев m к общему числу случаев n: р(А) = m/ n. Это определение вероятности сводится к появлению равновозможных событий. Однако чаще используют определение вероятности, связанное с частотой появления события m при многократном воспроизведении опыта n. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, заранее неизвестное. Условной вероятностью р(А/В) называется вероятность события А, вычисленная при условии, что произошло событие В. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого. Для независимых событий Теорема сложения вероятностей. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Для совместных событий: Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место: Формула полной вероятности. Вероятность события А, которое может произойти с одной из гипотез Н1,Н2…Нn, образующих полную группу несовместных событий, определяется выражением: Теорема гипотез Бейеса. Имеется полная группа несовместных гипотез Н1,Н2…Нn. Вероятности гипотез до опыта С помощью этой формулы переоцениваются вероятности гипотез На основе формулы Бейеса решаются задачи выделения сигналов на фоне помех, определения параметров возмущающих объектов, распознавания образов при обработке геофизических данных, оценки геолого-экономической эффективности геофизических методов и т. д. На практике часто используют геометрическую трактовку вероятности. Геометрическая вероятность обобщает классическое определение вероятности на бесконечное множество исходов эксперимента. К понятию геометрической вероятности приводит задача о бросании точки в некоторую ограниченную область G, содержащую в себе меньшую по размерам область g. Если событие А состоит в попадании точки в область g, то
Таблица 2.11.1. Таблица свойств вероятностей событий.
Некоторые сведения из теории информации. Наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации, называется теорией информации. Введем некоторые понятия теории информации. Энтропия - это мера степени неопределенности состояния некоторой физической системы. Любое сообщение является совокупностью сведений о некоторой физической системе. Если бы состояние физической системы было известно заранее, то не было бы смысла передавать сообщение. Пусть Х физическая система, которая случайным образом может оказаться в том или ином состоянии, т. е. системе Х присуща какая-то степень неопределенности состояния. Сведения тем ценнее и содержательнее, чем больше была неопределенность системы Х априори до их получения. Например, система «монета» может оказаться в одном из двух состояний «герб» или «решка». Система «кубик» (1, 2, 3, 4, 5, 6) имеет шесть возможных состояний. Поэтому неопределенность состояний «кубика» больше, чем у системы «монеты». Однако степень неопределенности состояний физической системы определяется не только числом ее возможных состояний, но и вероятностью этих состояний. Например, если запустить двигатель у технической системы «автомобиль», то вероятность того, что двигатель будет работать, равна 0,99. Двигатель будет продолжать работать и не заглохнет. Степень неопределенности состояния такой системы мала. В общем случае физическая система Х принимает состояния x1, x2, x3, …xn с вероятностями р1, р2, р3, …рn , где Эти данные удобно представлять в виде таблицы возможных состояний системы:
Таблица сходна с рядом распределения прерывной случайной величины Х с возможными значениями x1, x2, x3, …xn, имеющими вероятности р1, р2, р3, …рn. Для того чтобы свести физическую систему Х и случайную величину Х достаточно приписать каждому состоянию системы какое-то числовое значение, например, его номер. Для описания степени неопределенности состояния системы не важно, какие именно значения записаны значения в строках xi и pi. Важно их количество и их вероятности. Мерой априорной неопределенности состояния физической системы является энтропия. Энтропией системы называется сумма произведений вероятности различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:
где Знак минус перед суммой поставлен для того, чтобы энтропия была положительной, так как Перечислим основные свойства энтропии: - Энтропия обращается в ноль, когда одно из состояний системы достоверно, а другие невозможны. Действительно, если состояние системы в точности известно заранее, то все - При заданном значении n энтропия обращается в максимум. - Энтропия обладает свойством аддитивности, т. е. когда несколько физических систем объединяются в одну, то их энтропии складываются. При выборе основания логарифма равном двум за единицу измерения энтропии принимается энтропия системы «монета», т. е. энтропия физической системы, которая имеет два равновозможных состояния:
(2.11.2)
Действительно, по формуле (2.11.1):
Двоичная единица энтропии называется bit (binary digit – двоичный знак). Это энтропия одного разряда двоичного числа, которое может быть 0 или 1, или энтропия одной ячейки памяти на ферритах в вычислительных машинах. В качестве примера подсчитаем энтропию системы, имеющей n равновозможных состояний:
т. е. энтропия системы с равновозможными состояниями равна логарифму числа состояний. Другой пример, определить энтропию системы состоящей из двух методов (магниторазведки и гравиразведки), участвующих в геофизической съемке. В результате съемки система геофизических методов Х может оказаться в одном из четырех возможных состояний: оба измерения имеют высокие значения; магниторазведка имеет высокое значение, гравиразведка имеет низкое значение; гравиразведка имеет высокое значение, магниторазведка имеет низкое значение; оба измерения имеют низкие значения. Вероятности этих состояний равны: 0,2, 0,3, 0,4, 0,1. Запишем условия в виде таблицы состояний системы:
Для подсчета энтропии удобно использовать функцию Определим теперь максимальную возможную энтропию системы, состоящей из трех методов (магниторазведки, гравиразведки и электроразведки), каждый из которых может быть в четырех равновозможных состояниях. Общее число возможных состояний 4×4×4= 64. Согласно формуле (1.9.2) максимальная возможная энтропия такой системы равна Энтропия сложной системы Под объединением двух Таблица 2.11.3. Вероятности
Энтропия сложной системы по определению равна:
Если системы X и Y независимы, то по теореме умножения вероятностей, т. е. при объединении независимых систем их энтропии складываются.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.145.168 (0.009 с.) |

 , для нормального распределения геофизического поля. Таким образом, контрастность - это пиковое отношение сигнал-помеха. Из двух методов эффективнее тот, которым устанавливаются более контрастные аномалии.
, для нормального распределения геофизического поля. Таким образом, контрастность - это пиковое отношение сигнал-помеха. Из двух методов эффективнее тот, которым устанавливаются более контрастные аномалии. или энергетическое отношение
или энергетическое отношение  , где m – протяженность аномалии, определяемая величиной интервала корреляции. Если аномалии расплывчаты, то рассчитывают произведение контрастности аномалии на ее ширину или площадь. Площадь оценивается на уровне нижних значимых аномальных значений А min , контрастность определяется для каждого i -го пикета и суммируется по всей ширине
, где m – протяженность аномалии, определяемая величиной интервала корреляции. Если аномалии расплывчаты, то рассчитывают произведение контрастности аномалии на ее ширину или площадь. Площадь оценивается на уровне нижних значимых аномальных значений А min , контрастность определяется для каждого i -го пикета и суммируется по всей ширине 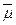 L или площади аномалии
L или площади аномалии 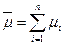 .
. , для гнейсов -
, для гнейсов -  . Возникает вопрос: можно ли надежно разделить эти объекты по плотности?
. Возникает вопрос: можно ли надежно разделить эти объекты по плотности?
 и формулу Бейеса
и формулу Бейеса  :
:
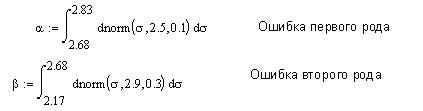
 . Для зависимых событий
. Для зависимых событий  .
. . В случае n событий:
. В случае n событий:  . Сумма вероятностей полной группы несовместных событий равна единице
. Сумма вероятностей полной группы несовместных событий равна единице  =1.
=1. .
.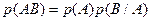 . Для независимых событий:
. Для независимых событий:  .
. .
. . В результате опыта появляется событие А. Вероятность гипотез после появления события А изменится и станет равной:
. В результате опыта появляется событие А. Вероятность гипотез после появления события А изменится и станет равной: 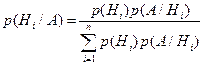 .
. , называемых априорными, т. е. известными до опыта. После проведения эксперимента, в результате которого появилось событие А, вероятности
, называемых априорными, т. е. известными до опыта. После проведения эксперимента, в результате которого появилось событие А, вероятности  называются апостериорными, т. е. полученными после опыта.
называются апостериорными, т. е. полученными после опыта. , где
, где  g и
g и 
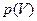
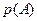



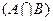

 Зависимые события
Зависимые события

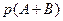
 - вероятность того, что система Х примет состояние x i Символом
- вероятность того, что система Х примет состояние x i Символом  будем обозначать событие, заключающееся в том, что система Х находится в состоянии x i. Очевидно, что
будем обозначать событие, заключающееся в том, что система Х находится в состоянии x i. Очевидно, что  .
. , (2.11.1)
, (2.11.1) .
. < 0 и
< 0 и  < 0. Основание логарифма может быть любым, а> 0. Перемена основания равносильна умножению энтропии на постоянное число, а выбор основания равносилен выбору единицы измерения энтропии, например, а = 10 - десятичная единица энтропии. Чаще используют двоичные единицы энтропии, которые хорошо согласуются с двоичной системой счисления вычислительных машин.
< 0. Основание логарифма может быть любым, а> 0. Перемена основания равносильна умножению энтропии на постоянное число, а выбор основания равносилен выбору единицы измерения энтропии, например, а = 10 - десятичная единица энтропии. Чаще используют двоичные единицы энтропии, которые хорошо согласуются с двоичной системой счисления вычислительных машин. . При этом
. При этом  . Неопределенность
. Неопределенность  при
при  раскрывается по правилу Лопиталя.
раскрывается по правилу Лопиталя.
 (2.11.2)
(2.11.2) , которая табулирована от 0 до 1 через 0,01. По формуле
, которая табулирована от 0 до 1 через 0,01. По формуле  , находим
, находим 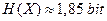 .
. .
. систем X и Y с возможными состояниями x1, x2, x3, …xn и y1, y2, y3, …ym понимается сложная система (X, Y), состояния которой (xi, yj) представляют собой все возможные комбинации состояний xi и yj. Число возможных состояний будет n× m. Обозначим
систем X и Y с возможными состояниями x1, x2, x3, …xn и y1, y2, y3, …ym понимается сложная система (X, Y), состояния которой (xi, yj) представляют собой все возможные комбинации состояний xi и yj. Число возможных состояний будет n× m. Обозначим  вероятность того, что система (X, Y) будет в состоянии (xi, yj). Вероятности
вероятность того, что система (X, Y) будет в состоянии (xi, yj). Вероятности 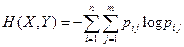
 откуда
откуда  и
и  ,
,


