
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы проверки статистических гипотезСодержание книги
Поиск на нашем сайте
Способ проверки статистических гипотез часто используется для разделения геологических объектов (гипотез) двух и более классов. Для осуществления способов проверки статистических гипотез необходимо знание плотностей распределения признаков геофизических полей, полученных ранее на эталонных объектах. В случае двух классов объектов (гипотез), например, Н 1- руда и Н 2 - не руда, сравниваются две гипотезы Н 1 и Н 2 путем нахождения коэффициента правдоподобия
где Для осуществления способа проверки статистических гипотез можно использовать формулу Бейеса. Апостериорная вероятность гипотезы Н 1 по формуле Бейеса:
где Если число классов более двух М > 2, то вычисления производятся по формуле Бейеса для полной группы гипотез (объектов):
Последовательно находят
Разделение объектов разных классов по гистограммам их физических свойств Надежность разделения геологических объектов разных классов оценивается по гистограммам их физических свойств. Если есть гипотезы Н 1 и Н 2, то ошибка первого рода a состоит в том, что при наличии объекта (гипотезы) Н 1 определя6тся объект Н 2. Ошибка второго рода b состоит в том, что при наличии объекта Н 2 определяется объект Н 1. Вероятности ошибок a и b определяются площадями под плотностью распределения признаков физических свойств объектов Н 1 и Н 2. В качестве примера на рис. 2.10.2 приведены значения вероятностей ошибок первого и второго рода a и b для двух объектов Н 1 и Н 2 при разделении признаков по среднему значению и дисперсии. В качестве признаков рассмотрены значения магнитного l = 1 Za (нТл) и гравитационного l = 2 g (мГл) полей.
Рис. 2.10.2. Вероятности ошибок первого и второго рода.
На рис. 2.10.2 приведены гистограммы двух геофизических полей Za и g над объектами двух классов Н 1 (руда) и Н 2 (помеха). В результате опыта измерено Za = 400 нТл, g = 10 мГл. Требуется установить, к какому классу относится геологический объект. Из гистограмм магнитных свойств объекта
В итоге точка x1, x2 принадлежит рудному объекту Н 1. Другой пример. При поисках нефтяной залежи использованы четыре признака: х 1 – пластовая скорость (v пл, м/с); х 2 – время последнего отражения (t,с); х 3 – число отражений (n); х 4 – отношение амплитуд отраженных волн (А1/А2). На рис. 2.10.3 приведены гистограммы объектов двух классов Н 1 (нефть) и Н 2 (помеха).
Рис. 2.10.3. Гистограммы объектов двух классов Н 1 (нефть) и Н 2 (помеха)
Для каждой i -й точки наблюдений найдены значения
По апостериорной вероятности гипотезы Под надежностью разделения объектов g понимается вероятность правильного разделения объектов. Если априорные вероятности классов Н 1 и Н 2 р 1 и р 2 равны р 1 = р 2 = 0,5, то вероятность общей безусловной ошибки Задача поисков объекта можно свести к задаче разделения объектов двух классов. При этом один класс объектов рассматривается как поисковый, а другой как помеха для поискового класса. Надежность выделения поискового объекта g l определяется по энергетическому отношению сигнал-помеха r l для l -го геофизического метода или l -го признака геофизического метода. При условии независимости признаков рассчитывается энергетическое отношение для комплекса методов:
Надежность поисков объекта комплексом методов увеличивается. По максимальной величине На шестом этапе формирования рационального комплекса геофизических методов (рис. 2.3.1) дается оценка геологической эффективности геофизических методов для решения поставленной геологической задачи.
|
||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.146 (0.007 с.) |

 , где
, где  - вектор независимых признаков
- вектор независимых признаков 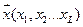 . Коэффициент правдоподобия подсчитывается по формуле:
. Коэффициент правдоподобия подсчитывается по формуле:
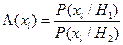 - частные коэффициенты правдоподобия, которые характеризуют относительный вклад каждого признака x l в общую величину
- частные коэффициенты правдоподобия, которые характеризуют относительный вклад каждого признака x l в общую величину  и
и  производится по гистограммам распределения вероятностей признака x l на эталонных объектах классов Н 1 и Н 2. Решение о принадлежности объекта в i -й точке наблюдений к классу Н 1 принимается согласно критерию максимального правдоподобия при
производится по гистограммам распределения вероятностей признака x l на эталонных объектах классов Н 1 и Н 2. Решение о принадлежности объекта в i -й точке наблюдений к классу Н 1 принимается согласно критерию максимального правдоподобия при  ,
,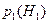 и
и  - априорные вероятности появления объектов Н 1 и Н 2. Полагая для априорных вероятностей
- априорные вероятности появления объектов Н 1 и Н 2. Полагая для априорных вероятностей  > 0,5 справедлива гипотеза Н 1. Если
> 0,5 справедлива гипотеза Н 1. Если  .
.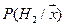 и по максимальной вероятности принимают решение о принадлежности к данному классу объектов. Априорные вероятности гипотез предполагаются равными друг другу для всех геологических объектов.
и по максимальной вероятности принимают решение о принадлежности к данному классу объектов. Априорные вероятности гипотез предполагаются равными друг другу для всех геологических объектов.
 = 24 нТл,
= 24 нТл, 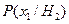 = 9 нТл. Из гистограмм силы тяжести
= 9 нТл. Из гистограмм силы тяжести  = 5 мГл,
= 5 мГл,  = 13 мГл. Из формулы для коэффициента правдоподобия для гипотезы Н 1 (руда):
= 13 мГл. Из формулы для коэффициента правдоподобия для гипотезы Н 1 (руда):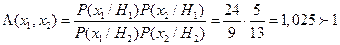

 и
и  , (l = 1, 2, 3, 4), где
, (l = 1, 2, 3, 4), где  и
и  и апостериорной вероятности гипотезы Н 1 (нефть)
и апостериорной вероятности гипотезы Н 1 (нефть)  ;
; 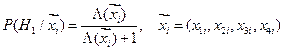
 , а надежность разделения g = 1-
, а надежность разделения g = 1- 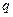 . При полном совпадении гистограмм
. При полном совпадении гистограмм  . Затем по
. Затем по  оценивается надежность разделения объектов двух классов комплексом методов:
оценивается надежность разделения объектов двух классов комплексом методов: .
. для различных сочетаний геофизических методов устанавливается наиболее эффективный комплекс в геологическом отношении.
для различных сочетаний геофизических методов устанавливается наиболее эффективный комплекс в геологическом отношении.


