
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условная энтропия объединения зависимых системСодержание книги
Поиск на нашем сайте Если объединяются зависимые системы, то энтропия объединения меньше энтропии составных частей. Обозначим
Условная энтропия системы Y зависит от того, какое состояние xi приняла система X. Всего таких возможных состояний n. Полную (среднюю) энтропию системы Y обозначим При геологическом картировании эффективность геофизических методов оценивается по количеству информации, содержащейся в геофизических данных. Расчет информативности геофизических методов основан на оценке среднего количества информации о системе геологических пород Y, содержащейся в сообщении о состоянии системы геофизических полей X Информация равна разности энтропий до и после получения сообщения о состоянии системы геофизических полей. Рассмотрим пример расчета информативности геофизических методов при геологическом картировании горных пород. Пусть имеются две системы Y и X объединенные в одну (X,Y). Y – система типов горных пород. X - система интервалов значений геофизического поля. Терригенные отложения системы горных пород сложены глинами y1, песчаниками, y2 и известняками y3. По одной из скважин выполнен каротаж ГК (рис. 2.11.2). Глины имеют повышенные значения радиоактивности x1 = 20-30 мкр/час и выше, песчаники средние значения радиоактивности x2 = 10-20 мкр/час, известняки низкие значения радиоактивности x3 = 0-10 мкр/час. Вероятности состояния системы (X,Y) при измерении естественной радиоактивности горных пород
Рис. 2.11.2. Результаты каротажа ГК терригенных отложений горных пород: y1 – глины (синий цвет), y2 - песчаники (зеленый цвет), y3 -известняки (желтый цвет).
Таблица 2.11.3 Вероятности
Вероятности
где
В таблице (2.11.3) приведены значения Таблица 2.11.4. Условные вероятности
Теперь можно подсчитать полную энтропию системы горных пород Y после выполнения всех измерений естественной радиоактивности геофизического поля X. После вычислений Энтропия и информация При выполнении геофизических измерений наблюдаем систему X, связанную с системой исследуемых горных пород Y. Любые сведения (информация) о геофизических полях X, измеренных над горными породами Y, уменьшают неопределенность исследуемой системы горных пород Y. Какую информацию о системе Y дают геофизические наблюдения X? Определим эту информацию, как уменьшение энтропии системы горных пород Y в результате получения сведений о X. Если до получения информации (априори) энтропия системы X была
Естественно каждое слагаемое Измеряя информацию в двоичных единицах, мы характеризуем ее числом ответов «да» или «нет». Действительно, чтобы выяснить состояние системы «монета» (1.9.2) надо задать один вопрос: находится ли система в состоянии x1? Ответ «да» или «нет» доставляет информацию, которая достигает своего максимального значения равного единице, когда оба состояния априори равновероятны р1 = р2 = 0,5. т. е. максимальная информация даваемая ответом «да» или «нет» равна одной двоичной единице. Если информация равна n bit, то она равносильна информации даваемой ответами n ответами «да, нет» поставленных так, что «да» или «нет» одинаково вероятны. В предыдущем примере относительная информация, доставляемая гамма-каротажем На седьмом этапе формирования рационального комплекса геофизических методов (рис. 2.3.1) дается оценка экономической эффективности геофизических методов для решения поставленной геологической задачи.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 676; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 условную вероятность того, что система Y примет состояние yj при условии, что система xi находится в состоянии xi.
условную вероятность того, что система Y примет состояние yj при условии, что система xi находится в состоянии xi.  . Условную энтропию системы Y при условии, что система X находится в состоянии xi, обозначим
. Условную энтропию системы Y при условии, что система X находится в состоянии xi, обозначим 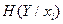 . По определению энтропии:
. По определению энтропии:
 . Система Y может принимать разные состояния в зависимости от вероятности рi состояний xi системы X. По определению среднего значения:
. Система Y может принимать разные состояния в зависимости от вероятности рi состояний xi системы X. По определению среднего значения:  .
.  задаются таблицей 2.11.3:
задаются таблицей 2.11.3:
 объединения систем (X,Y) при измерении естественной радиоактивности горных пород
объединения систем (X,Y) при измерении естественной радиоактивности горных пород
 - вероятность того, что система горных пород Y примет значение y j;
- вероятность того, что система горных пород Y примет значение y j; - вероятность того, что система геофизического поля X примет значение x i;
- вероятность того, что система геофизического поля X примет значение x i; - вероятность совместного наблюдения горной породы y j и геофизического поля x i;
- вероятность совместного наблюдения горной породы y j и геофизического поля x i; - геометрическая вероятность того, что случайно брошенная точка оказалась в горной породе y j;
- геометрическая вероятность того, что случайно брошенная точка оказалась в горной породе y j; - геометрическая вероятность того, что случайно брошенная точка оказалась в геофизическом поле x i;
- геометрическая вероятность того, что случайно брошенная точка оказалась в геофизическом поле x i; - геометрическая вероятность того, что случайно брошенная точка оказалась одновременно в горной породе y j и геофизическом поле x i;
- геометрическая вероятность того, что случайно брошенная точка оказалась одновременно в горной породе y j и геофизическом поле x i; - полная длина профиля наблюдений.
- полная длина профиля наблюдений. , откуда следует, что условные вероятности
, откуда следует, что условные вероятности  . В результате получим таблицу условных вероятностей
. В результате получим таблицу условных вероятностей 
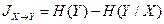 , где
, где  , а после получения сведений путем измерения геофизических полей, состояние системы X полностью определилось, т. е. энтропия стала равной нулю, то количество информации JX, доставленной геофизическими измерениями, равно энтропии этой системы:
, а после получения сведений путем измерения геофизических полей, состояние системы X полностью определилось, т. е. энтропия стала равной нулю, то количество информации JX, доставленной геофизическими измерениями, равно энтропии этой системы: 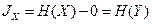 . Таким образом, количество информации, приобретаемое при полном выяснении состояния системы X равно энтропии этой системы:
. Таким образом, количество информации, приобретаемое при полном выяснении состояния системы X равно энтропии этой системы:
 рассматривать, как частную информацию
рассматривать, как частную информацию  отдельного сообщения о том, что система X находится в состоянии xi. Тогда
отдельного сообщения о том, что система X находится в состоянии xi. Тогда 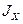 будет полной (средней) информацией, получаемой от всех возможных сообщений о системе X с учетом их вероятностей. Если все возможные состояния системы X априори равновероятны р1. р2. …рi =1/n, то частная информация от отдельного сообщения:
будет полной (средней) информацией, получаемой от всех возможных сообщений о системе X с учетом их вероятностей. Если все возможные состояния системы X априори равновероятны р1. р2. …рi =1/n, то частная информация от отдельного сообщения:  равна полной (средней) информации о системе X:
равна полной (средней) информации о системе X:  .
. равна 0,5716/1,42 @ 60 %. Сравнивая относительные информации отдельных геофизических методов между собой, находят наиболее информативный геофизический метод для решения вопросов геологического картирования горных пород.
равна 0,5716/1,42 @ 60 %. Сравнивая относительные информации отдельных геофизических методов между собой, находят наиболее информативный геофизический метод для решения вопросов геологического картирования горных пород.


