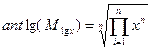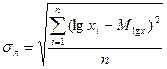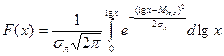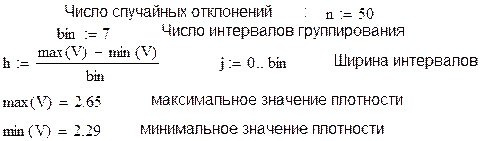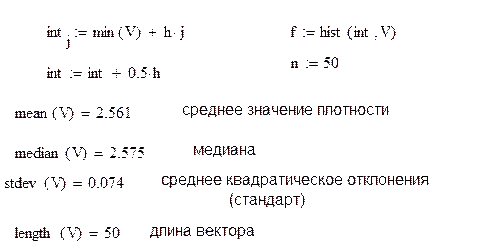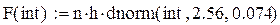Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физических свойств горных породСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимым и достаточным условием успешного применения геофизических методов является заметная дифференциация (контрастность) физических свойств горных пород в районе работ. Физические свойства пород зависят от многих геологических факторов: возраста, глубины залегания, метаморфизма горных пород, степени их выветренности, пористости, влагонасыщенности и т.д. По этой причине частные значения физических параметров обычно колеблются в широких пределах. Для получения достаточной представительности результатов необходимо, чтобы измерения носили массовый характер. Для каждой разновидности горных пород желательно иметь не менее 30-50 определений. Физические свойства определяются обычно путем исследований на образцах, в естественном залегании (параметрические замеры), по данным каротажа и по итогам интерпретации результатов полевых геофизических наблюдений соответствующими методами. Образцы берут из коренных обнажений пород и руд, по возможности слабо затронутых вторичными процессами. Места отбора образцов равномерно распределяют по площади и отмечают на карте с целью изучения закономерностей изменения физических параметров по площади исследований. Изменчивость физических свойств пород и руд обуславливает широкое использование статистических методов обработки с целью компактного представления данных о физических свойствах, выявления в общей совокупности самостоятельных групп пород, определения доверительных границ изменения физических параметров горных пород, установления корреляционных зависимостей между различными физическими параметрами и изучения зависимостей физических свойств от состава и структуры горных пород.
Эмпирические распределения. Множество значений физического признака, обладающего свойствами случайной величины, будем называть статистической совокупностью. В статистической совокупности значения физического признака располагаются в порядке их получения и записи при изучении геологического объекта поисков. Для удобства математической обработки производят упорядочение статистической совокупности, которое заключается в том, что отдельные значения признака располагаются в возрастающем или убывающем порядке. Упорядочение совокупностей непрерывных физических признаков производится методом группирования и последующего построения вариационных рядов и соответствующих им графиков. Упорядочение непрерывных физических признаков производится в интервальной форме. Число интервалов m можно оценить по формуле: m = 1+3.33 lgN, где N - объем выборки. Для выбора ширины интервала группирования используется формула Стурджесса:
где xmаx и xmin - максимальное и минимальное значение физического параметра x. Вычисленные значения Δ x - округляют до удобной величины. Вариационный ряд статистической совокупности физического признака представляется в виде таблицы, в которой в возрастающем порядке перечислены интервалы или середины интервалов группирования и соответствующие им частоты и частости встречи физических признаков. Перед составлением таблицы вычисляют значения середины интервалов группирования по формуле:
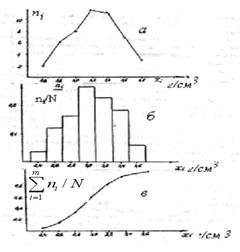
где a i и b i, соответственно, начало и конец i -го интервала группирования, подсчитывают частоту n i и частость ωi = ni /N попадания физического признака в i -й интервал группирования. Для компактного и наглядного представления результатов массовых измерений физических свойств горных пород вариационный ряд может быть представлен графически в виде полигона, гистограммы или кумуляты. Полигоном называется ломаный график, построенный в декартовой системе координат. По оси абсцисс откладываются в возрастающем порядке середины интервалов группирования физического параметра, а по оси ординат соответствующие им частоты или частости. Гистограммой вариационного ряда называется ступенчатый график, состоящий из серии примыкающих друг к другу прямоугольников с основаниями на оси абсцисс, равными ширине интервала группирования, и высотами по оси ординат, соответствующими значениям частот или частостей. Кумулятой называют монотонно растущий график, который образуется, если по оси абсцисс откладывать середины интервалов группирования, а по оси ординат сумму частот или частостей с нарастающим итогом. В качестве примера построения полигона, гистограммы и кумуляты вариационного ряда ниже приведены примеры распределения плотности перидотитов Баженовского месторождения хризотил-асбеста (рис. 2.5.1)
Рис. 2.5.1. Пример построения полигона (а), гистограммы (б) и кумуляты (в) вариационного ряда распределения плотности перидотитов Баженовского месторождения хризотил-асбеста
Наряду с построением вариационных рядов и графиков при обработке результатов измерений физических свойств горных пород вычисляются статистические характеристики положения (средняя величина, медиана, мода) и рассеяния результатов измерений (дисперсия, стандарт, коэффициент вариации, показатель асимметрии и показатель эксцесса). Средняя величина
где m – число интервалов группирования вариационного ряда. Медиана - значение признака, соответствующее середине упорядоченного вариационного рада. Медиана делит упорядоченную Мода - значение признака, которое характеризуется наибольшей частотой или частостью и совпадает с абсциссой максимума вариационной кривой. Статистические характеристики рассеяния указывают на степень и характер концентрации или рассеяния отдельных значений физического параметра относительно характеристик положения. Дисперсия - это средний квадрат отклонения отдельных вариант от среднего значения. Дисперсия вычисляется по формуле:
где m – число интервалов группирования вариационного ряда. Стандарт это среднее квадратическое отклонение, равное корню квадратному из дисперсии.
Теоретические распределения. Результаты измерений физических свойств горных пород осложнены погрешностями наблюдений, поэтому они носят случайный характер и обладают свойствами случайной величины. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, заранее неизвестное. Если перечислить все возможные значения случайной величины и указать вероятности этих значений, то получится распределение случайной величины. Характеристикой непрерывной случайной величины является плотность вероятности f(x), с которой распределяются её значения в окрестности данной точки x. Плотность распределения вероятностей называют дифференциальной функцией распределения или дифференциальным законом распределения. Кривая, изображающая плотность распределения случайной величины, называется дифференциальной кривой распределения. Вероятность того, что случайная величина x примет значение, лежащее в границах от а до d, равна определённому интегралу в тех же пределах от плотности:
Кроме дифференциальной функции распределения вероятностей часто используется кумулятивная функция распределения случайной величины, которая подсчитывается по формуле
Кумулятивная функция непрерывной случайной величины характеризует вероятность того, что случайная величина x примет значение меньше X. Кумулятивная функция распределения называется также интегральной функцией или интегральным законом распределения вероятностей. Она является универсальной характеристикой случайной величины. Кумулятивная функция монотонно возрастает в пределах от нуля до единицы. Аналогично статистическим характеристикам при описании случайных величин вводятся их числовые характеристики (математическое ожидание, дисперсия и среднее квадратическое отклонение). Математическое ожидание M x непрерывной случайной величины определяется формулой:
Математическое ожидание является мерой положения и эквивалентно среднему значению вариационного ряда. Дисперсия D x непрерывной случайной величины характеризует степень рассеяния отдельных значений от математического ожидания случайной величины ожидания и определяется формулой
Среднее квадратическое отклонение s x равно корню квадратному из дисперсии Статистические характеристики вариационных рядов при достаточной статистике отсчетов стремятся, как к пределу, к числовым характеристикам случайных величии, распределение которых является предметом исследования теории вероятностей и носит закономерный характер. Законы распределения случайной величины могут быть различными. Для непрерывных случайных величин, к которым относятся физические свойства горных пород, чаще всего встречается нормальное (Гауссово) распределите и логарифмически нормальное распределение случайной величины. Случайная величина x распределена нормально, если функция плотности вероятности f(x) имеет вид
где Mx - математическое ожидание, σ x - среднее квадратическое отклонение (стандарт). Математическое ожидание соответствует среднему арифметическому отдельных измерений случайной величины
Стандарт подсчитывается по формуле:
Функция нормального распределения характеризуется двумя параметрами М x и σx и имеет колоколообразную форму. Параметр М x не оказывает влияние на форму кривой f(x), но смещает ее вдоль оси x. Параметр σx определяет вытянутость или сжатость кривой f(x) по оси x. Математическое ожидание величины x совпадает с модой М о и медианой Ме , т. е. Мx = Мо = Ме. Заменой переменных t = (x-Mx/σx) любое нормальное распределение может быть приведено к простейшему виду:
Такое преобразование переменной называется нормированием случайной величины к её среднему квадратическому отклонению. При этом начало отсчета переносится в точку М x, а в качестве единицы масштаба используется среднее квадратическое отклонение σx. Нормированная кумулятивная функция нормального распределения подсчитывается по формуле
где y = lg x, My - математическое ожидание случайной величины у; σл - среднее квадратическое отклонение lg x от его математического ожидания (логарифмический стандарт). Математическое ожидание lg x соответствует среднему геометрическому самой случайной величины x.
Логарифмический стандарт подсчитывается по формуле
Кривая логарифмически нормального распределения имеет правостороннюю асимметрию, причем М о < М е < Мx. Эта кривая симметризуется с помощью логарифмического масштаба по оси абсцисс. Кумулятивная функция логарифмически нормального распределения имеет вид:
Сопоставление эмпирических и теоретических распределений. Распределение физических параметров однородного геологического объекта чаще всего подчиняется нормальному закону (например, распределение плотности горных пород) или логнормальному закону (например, распределение магнитной восприимчивости, удельного электрического сопротивления, концентрации химических элементов). Для правильной обработки результатов измерений необходимо знать, какому закону соответствует распределение данного физического свойства. В случае нормального закона распределения при построении вариационных кривых интервалы группирования физических свойств выбираются равными между собой в линейном масштабе. Для сравнения распределений графики накопления частостей иногда удобно строить на вероятностном трафарете, который характеризуется вероятностной шкалой по оси ординат. На вероятностном трафарете нормальное распределение имеет вид прямой линии. Сопоставление результатов эксперимента в виде гистограммы накопления частостей с теоретически нормальным распределением приведены на рис. 2.5.2.
Рис. 2.5.2. Характер экспериментальных (штриховые кривые) и теоретических нормальных (сплошные кривые) распределений физического свойства x в виде гистограммы (а), графиков накопления частостей в обычном масштабе (б) и на вероятностном бланке (в)
Рассмотрим порядок построения гистограмм распределения частостей в редакторе Mathcad. Введем некоторые обозначения, принятые в редакторе Mathcad.
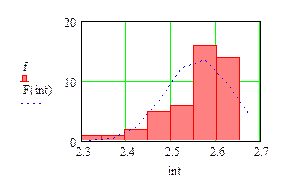
Ниже в редакторе Mathcad построено подходящее нормальное распределение (рис. 2.5.3). Функция вычисления плотности распределения вероятности нормального распределения подсчитывается по формуле dnorm(x, m, s), где m - среднее значение, s - среднеквадратическое отклонение,
Рис. 2.5.3. Определение плотности гранитов в поселке В. Сысерть на базе геофизической практики студентов УГГУ: Ось x - интервалы группирования, Ось y – вероятность, %
В соответствии со схемой поэтапного формирования рационального комплекса геофизических методов (рис. 2.3.1) формирование начинается с построения априорной ФГМ объекта поисков.
|
||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.247.59 (0.008 с.) |

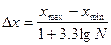
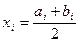
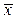 характеризует массовый уровень физического признака в статистической совокупности. Для вариационных рядов совокупностей с непрерывным или дискретным признаком средняя величина признака подсчитывается, как средняя взвешенная по формуле:
характеризует массовый уровень физического признака в статистической совокупности. Для вариационных рядов совокупностей с непрерывным или дискретным признаком средняя величина признака подсчитывается, как средняя взвешенная по формуле: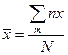
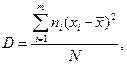
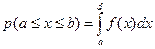
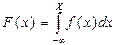
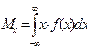
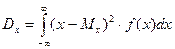
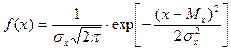
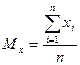
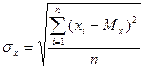
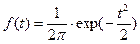
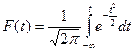
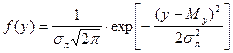 Непрерывная случайная величина x распределена логарифмически нормально, если логарифмы ее значений распределены по закону Гаусса:
Непрерывная случайная величина x распределена логарифмически нормально, если логарифмы ее значений распределены по закону Гаусса: