Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комплексная интерпретация геофизических наблюдений с использованием функции комплексного показателя (ФКП)Содержание книги
Поиск на нашем сайте
Функция комплексного показателя (ФКП) представляет собой результат смешения сигналов разной природы Q, выраженных в цифровой форме. ФКП применяется в тех случаях, когда объект исследований не создает устойчивых сигналов в полях разных методов, когда эти сигналы малы и сопоставимы с инструментальными и геологическими помехами. Основные принципы комплексной интерпретации геофизических данных с использованием ФКП разработаны Г. С. Вахромеевым [3,4]. Функция комплексного показателя служит для свертывания информации, полученной несколькими геофизическими методами, приведения наблюдений к уровню нормального поля, выделения слабых аномалий на фоне помех и разделения выявленных комплексных аномалий на перспективные и неперспективные. Для определения ФКП необходимо предварительно перевести результаты всех частных методов в равноточные безразмерные величины показателей контрастности γ. Показатель контрастности j -го метода в i -ой точке подсчитывается по формуле
где γ ji - показатель контрастности j -го метода в i -ой точке; Aji - значение j -го измеренного признака в i -ой точке профиля; Aj - среднее арифметическое значение j -го признака в области фона; S j - стандарт j -го признака, который подсчитывается по формуле:
где n - число измерений j -го признака по профилю. Преимуществом использования понятия контрастности в виде (1), когда значения сигнала нормируются по стандарту, является то, что значения показателя контрастности γ ji распределены по закону Гауcса с нулевым средним Вид функции комплексного показателя выбирается над эталонным объектом по материалам натурного моделирования или, исходя из ФГМ искомого объекта так, чтобы добиться максимальной контрастности аномалий ФКП над объектом при одновременном подавлении аномалий ФКП над объектами - помехами. В зависимости от формы и знака аномалий отдельных методов различают несколько возможных случаев. Полезные сигналы частных методов имеют примерно одинаковую форму и одинаковый знак. В этом случае
где Qi – значение ФКП в i -ой точке профиля; p - количество частных методик; γji - показатель контрастности j -го частного метода в i -ой точке профиля в безразмерных величинах показателя контрастности.
Примером для рассматриваемого случая могут служить аномалии Δg и Δ Z над вертикально намагниченным шаром с избыточной плотностью, которые имеют сходный вид. Полезные сигналы частных методов имеют примерно одинаковую форму, но различны по знаку, тогда
Примером для рассматриваемого случая может служить положительная гравитационная аномалия и отрицательная аномалия естественного электрического поля над залежью медных колчеданов. Полезные аномалии частных методов имеют примерно одинаковую форму и одинаковый знак, но для некоторых методов наличие сигнала является не положительным, а отрицательным фактором контроля искомого объекта. В этом случае:
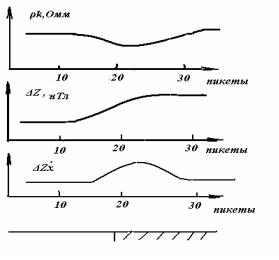
где p и q - число методов, аномалии которых являются, соответственно, положительными и отрицательными факторами контроля искомого объекта. Например, при поисках сульфидных кобалъто-пиритовых зон, положительные аномалии ΔZ являются фактором неперспективности оруденения, так как связаны с дайками диабазов. Перевод магниторазведки в разряд негативных факторов подчеркивает комплексную аномалию над кобальто-пиритовыми рудами и одновременно подавляет неперспективные ореолы кобальта над дайками диабазов, которые в рассматриваемом случае относятся к разряду помех. Полезные сигналы различны по форме и знаку. В этом случае один из сигналов обрабатывается так, чтобы в результате обработки его вид был сходен с видом других сигналов. Например, контакт двух горных пород выделяется по данным электроразведки (СЭП) минимумом. По данным магниторазведки Δ Z аномалия имеет вид ступени, рис. 1.13.1. Для получения сходных кривых достаточно результаты магниторазведки графически продифференцировать:
а затем перейти к расчету ФКП по формуле, соответствующей второму случаю (2.13.4):
Рис.1.13.1. Пример обработки сигналов при подсчете ФКП над обводненным контактом двух горных пород различного намагничения
Другим примером использования ФКП может служить мощный намагниченный пласт с избыточной плотностью. Он выделяется по данным гравитационной разведки положительной аномалией Δ g. По данным магниторазведки аномалия Δ Z имеет несимметричный вид с двумя экстремумами. Для получения сходного вида кривых из аномалии Δ Z следует выделить кривую арктангенсов и после этого перейти к подсчету ФКП по формуле (2.13.3) Q = γΔg + γarctgΔZ
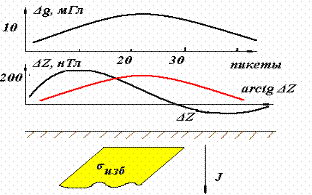
Пример обработки сигналов при подсчете ФКП над мощным наклонным вертикально намагниченным пластом с избыточной плотностью приведен на рис.1.13.2..
Рис. 1.13.2 Использование ФКП для различных по форме сигналов.
Учет знака полезных сигналов можно осуществить также с помощью ФКП, заданной в виде квадратов контрастностей аномалий отдельных методов. При этом подсчет ведется по формуле
где p и q - число методов, аномалии которых являются, соответственно, положительными и отрицательными факторами контроля искомого объекта. Значимость результата оценивается по критерию χ2 (хи -квадрат). При Q2 > χ2 аномалия Q2 значима. Возможности методики задания ФКП в виде квадратов контрастностей отдельных методов рассмотрены на модельном примере, рис. 1.13.3, где решается задача поисков кимберлитовых тел в траппах по данным магниторазведки Δ Z и электроразведки ρk.Согласно физико-геологической модели кимберлитовой трубки над ней ожидается положительная аномалия ΔZ и пониженное значение ρk. В каждом из методов отмечаются интенсивные помехи, превосходящие по величине аномалию от кимберлитовой трубки. На графике суммарного поля полезный сигнал визуально не обнаруживается. Расчет функции комплексного показателя в виде Q 2 дает в центральной части профиля отчетливую аномалию, надежно превышающую предельную величину χ2 -критерия, который при 2%-ном уровне значимости равен 10. Аномалия ФКП в виде Q 2 позволяет локализовать местоположение кимберлитовой трубки.
Рис. 1.13.3. Модельный пример использования ФКП в виде Q 2 при поисках кимберлитовых тел в траппах: 1 - вид искомой аномалии от кимберлитовых тел 2 - график помехи, 3 - суммарный сигнал аномалии и помехи
Поисковым признаком может служить изрезанность кривой геофизического метода по профилю наблюдений. Такие измерения предварительно преобразуются в графики дисперсий или стандарта. Например, редкометальные пегматитовые жилы выделяются повышенной дисперсией магнитного поля, повышенным содержанием урана и пониженным содержанием тория. Значения Δ Z i пересчитываются в стандартные отклонения способом скользящего окна в три пикета:
Затем подсчитывается контрастность ФКП по формуле:
Рис. 1.13.4. Редкометальные пегматитовые жилы.
Кроме геофизических можно использовать и качественные признаки ФКП. Качественный признак объекта определяется функцией телеграфных сигналов j(x) [10]: если признак есть Введем понятие показателя контрастности ФКП = Q соотношением
где γQi - показатель контрастности ФКП в i -oй точке профиля; Q i - значение ФКП в i -ой точке профиля; Q ф - фоновое значение ФКП; S Q - стандарт ФКП.
Значимость аномалий ФКП оценивается по нижнему аномальному пределу Qa = 3SQ, где SQ - стандартное отклонение ФКП. Для аномалий коррелированных по n точкам или профилям (n ≤ 9) нижний аномальный предел можно снизить. Он будет равен Преимуществом использования ФКП является то, что контрастность аномалий ФКП существенно превышает контрастность аномалий отдельных методов. Амплитуда аномалий ФКП складывается из амплитуд аномалий отдельных методов. Она пропорциональна числу методов, т. е. Q ~ m, где m - число методов. Если значения сигналов отдельных методов представлены в виде показателей контрастности, то дисперсии их единичны, т. е. D(γ1) = D(γ2) = D(γ3) = ××× = D(γm) = 1,. При этом дисперсия ФКП для некоррелированных признаков будет равна:
откуда следует
При подсчете ФКП показатели отдельных методов суммируются. Поскольку фоновые значения показателей контрастности отдельных методов равны нулю, то и сумма их равна нулю, т. е. фоновые значения ФКП равны нулю Q ф = 0. При этом контрастность ФКП будет Контрастность аномалии ФКП можно ещё повысить трансформацией Если n число точек в сглаживающем окне, то вычисление скользящего среднего уменьшает дисперсию фона в n раз. Действительно, контрастность сглаженной аномалии будет
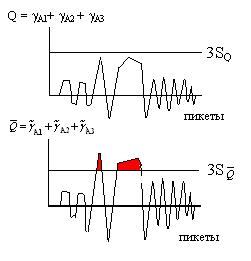
где Подставляя Таким образом, простое сглаживание измеренных значений по n точкам повышает контрастность аномалии ФКП в √ n раз. На рис. 1.13.5 приведены результаты сглаживания исходных данных по трем точкам. На модельных примерах аномалий отдельных геофизических методов А 1, А 2, и А 3 наложены среднеквадратические погрешности наблюдений. Размер наложенных погрешностей соответствует 1S, 2S и 3S стандартным среднеквадратическим погрешностям наблюдений отдельных методов. Функция комплексного показателя подсчитывалась путем сложения контрастностей аномалий отдельных методов. ФКП без сглаживания исходных данных не превышает трех стандартных погрешностей ФКП. После предварительного сглаживания исходных данных по трем геофизическим методам ФКП позволяет выделить искомую аномалию.
Рис. 1.13.5. Результаты сглаживания исходных данных по трем точкам: Q = gA1+ gA2 + gA3 - результаты ФКП без сглаживания;
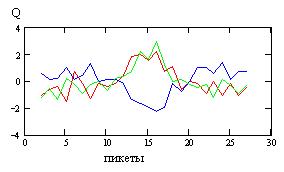
Рассмотрим еще один пример использования ФКП. Определим на профиле местоположение вероятной залежи медноколчеданной руды путем вычисления ФКП. Полевые измерения проводились тремя методами: магнитометрией ΔZ, гравиметрией Δg и электрометрией (метод вызванных потенциалов h). Из значений Δg и Δ Т предварительно была исключена региональная составляющая поля. Требуется определить структуру ФКП, учитывая следующие физико-геологические условия. Залежь медноколчеданнсй руды имеет форму крутопадающей линзы небольшой мощности до 15 метров в поперечнике, залегает внутри вулканогенной толщи и имеет первичный ореол сульфидной минерализации вдоль плоскости линзы. На участке залежи наблюдается повышение электропроводности и поляризуемости горных пород. Руда представлена массивным медным и серным колчеданом. Минералы магнетита и пирротина в области залежи отсутствуют. Таким образом, зона рудной залежи характеризуется избыточной плотностью и относительным понижением магнитных свойств. Рудовмещающая толща покрыта рыхлыми осадками с переменной мощностью 10-20 м. Амплитуды показателей контрастности отдельных геофизических методов не превосходят величину тройного стандарта фона для этих методов и не позволяют надежно выделить аномалию от рудной залежи отдельными методами (рис 1.13.6). Поэтому был подсчитан показатель контрастности для всего комплекса методов ΔZ, Δg и h. Затем был выбран подходящий вид функции комплексного показателя для заданного комплекса геофизических методов
Рис. 1.13.6. Контрастность отдельных методов по профилю измерений: 1. электроразведка h - красный цвет; магниторазведка ΔZ – синий цвет; 3. гравиразведка Δg - зеленый цвет.
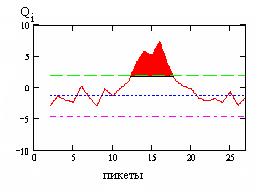
Рис. 1.13.7. Контрастность суммарного ФКП комплекса методов электроразведки, магниторазведки и гравиразведки Q i: среднее значение ФКП – синий цвет; максимальная амплитуда ФКП - зеленый цвет; минимальная амплитуда ФКП - оранжевый цвет
На восьмом этапе формирования рационального комплекса геофизических методов (рис. 2.3.1) выбирается собственно рациональный комплекс геофизических методов для решения поставленной геологической задачи. На девятом этапе формирования рационального комплекса геофизических методов выполняются измерения физических полей на базе выбранного комплекса геофизических методов. На десятом этапе формирования рационального комплекса геофизических методов получаются новые геолого-геофизические результаты, и строится апостериорная ФГМ объекта поисков.
ЛИТЕРАТУРА
1. Боровко Н. Н. Оптимизация геофизических исследований при поисках рудных месторождений. – Л.: Недра, 1979. 2. Бродовой В. В. Геофизические исследования в рудных провинциях. – М.: Недра, 1984. 3. Вахромеев Г. С. Общие принципы комплексирования геофизических методов при поисках рудных месторождений. – Иркутск: Изд-во ИПИ, 1970. – 119 с. 4. Вахромеев Г. С. Основы методологии комплексирования геофизических исследований при поисках рудных месторождений. – М.: Недра, 1978. – 152 с. 5. Геофизические методы исследования скважин: справочник геофизика / под ред. В. М. Запорожца. – М.: Недра, 1983. 6. Гнеденко Б. В. Курс теории вероятностей. – М.: ГИФМЛ, 1961. 406 с. 7. Кассин Г. Г. Геофизические методы на региональном этапе геологоразведочного процесса: курс лекций. – Екатеринбург: Изд-во УГГГА, 1996. – 104 с. 8. Крылатков С.М. Теоретические основы обработки геофизической информации. Курс лекций для бакалавров. – Екатеринбург: Изд-во УГГГА, 1997. – 200 с. 9. Комплексирование методов разведочной геофизики: справочник геофизика / под ред. В. В. Бродового, А. А. Никитина. – М.: Недра, 1984. 10. Матерон Ж. Основы прикладной геостатистики. – М., «Мир», 1968. – 408 с. 11. Савинский И. Д. таблицы вероятностей подсечений эллиптических объектов прямоугольной сетью наблюдений. – М.: «Недра», 1964. – 86 с. 12. Тархов А. Г., Бондаренко В. М., Никитин А. А. Комплексирование геофизических методов. – М.: Недра, 1982. 13. Физические свойства горных пород и полезных ископаемых: справочник геофизика / под ред. Н. Б. Дортман. – М.: Недра, 1976. 14. Давыдов Ю. Б. Теоретические основы комплексирования геофизических методов // Методические указания к практическим занятиям. Часть 1. – Свердловск: Изд-во СГИ, 1989. – 46 с. 15. Давыдов Ю. Б., Талалай А. Г., Кассин Г. Г. Теоретические основы комплексирования геофизических методов // Методические указания к самостоятельной работе. Часть 2. Оценка геологической информативности геофизических методов. – Свердловск: Изд-во СГИ, 1990. – 40 с.
СОДЕРЖАНИЕ стр. Предисловие……………………………………………………… 3 Принятые сокращения, условные обозначения …………….4 Введение………………………………………………………….. 5 1. Классификация геофизических методов поисков и разведки месторождений полезных ископаемых……………………..………..5 2. Понятие физико-геологической модели (ФГМ)…………… … …8 2.1. Априорная ФГМ объекта поисков…………………. ……….17 2.2. Примеры построения и численного расчета ФГМ для тел с известной геометрической формой………………………… …………….18 2.2.1. Гравитационное поле сферической залежи с избыточной плотностью…………………………………………………………..18 2.2.2. Магнитное поле вертикально намагниченного шара…………….20 2.2.3. Магнитное поле косо намагниченного шара………………………22 2.2.4. Магнитное поле пласта большой мощности…………………… 25 2.2.5. Магнитное поле наклонного мощного пласта произвольного намагничения…………………………………………………………………….…29 2.2.6. Электрическое поле проводящей сферы……………………… …30 2.3. Принципы комплексирования геофизических данных и этапы формирования рационального комплекса геофизических методов… ………..31 2.4. Нормальное геофизическое поле, аномалия, помеха……………….34 2.5. Статистическая обработка результатов измерений физических свойств горных пород………………………………………..…….41 2.6. Построение априорной ФГМ объекта поисков…………………….48 2.7. Условия применимости геофизических методов для решения геологической задачи……………………………………………………52 2.8. Исследование неоднозначности решения геологической задачи отдельными методами…………………………………….………………59 2.9. Расчет оптимальной сети наблюдений и точности измерений……65 2.10. Обработка и интерпретация геофизических наблюдений для решения поставленной геологической задачи………………………….…71 2.11. Оценка геологической эффективности геофизических методов..81 2.12. Оценка экономической эффективности геофизических методов для решения поставленной геологической задачи…………………..91 2.13. Комплексная интерпретация геофизических наблюдений с использованием функции комплексного показателя (ФКП)……………… 93 Литература………………………………………………………………. 98
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 870; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.183.235 (0.009 с.) |

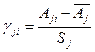 (1.13.1)
(1.13.1)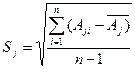 (1.13.2)
(1.13.2)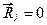 и единичным стандартом Sj = 1.
и единичным стандартом Sj = 1.
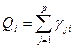 (1.13.3)
(1.13.3)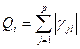 (1.13.4)
(1.13.4)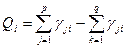 (1.13.5)
(1.13.5)
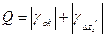
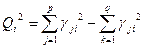 (1.13.6)
(1.13.6)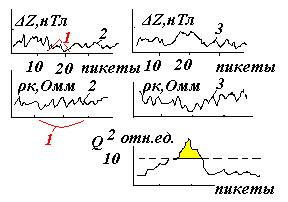
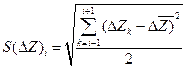 (1.13.7)
(1.13.7)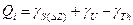 , где
, где 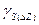 - контрастность стандарта магнитного поля. На рис. 1.13.4 приведены результаты построения ФКП по данным магниторазведки ΔZ и металлометрии СU , CTh по профилю над редкометальными пегматитовыми жилами. Жилы в левой части профиля обнаружены по данным геофизики.
- контрастность стандарта магнитного поля. На рис. 1.13.4 приведены результаты построения ФКП по данным магниторазведки ΔZ и металлометрии СU , CTh по профилю над редкометальными пегматитовыми жилами. Жилы в левой части профиля обнаружены по данным геофизики.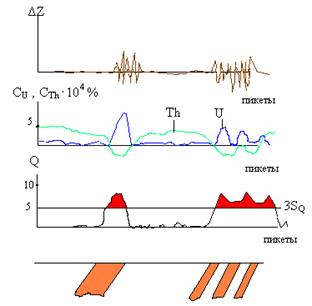
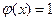 , если признака нет
, если признака нет 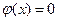 . Функция телеграфных сигналов сглаживается скользящим средним арифметическим по трем точкам (1.11.7) и используется как признак при расчете ФКП.
. Функция телеграфных сигналов сглаживается скользящим средним арифметическим по трем точкам (1.11.7) и используется как признак при расчете ФКП. (1.11.8)
(1.11.8)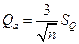 .
.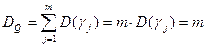
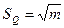
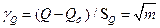 . Таким образом, контрастность аномалии ФКП в √m раз больше, чем контрастность отдельных методов.
. Таким образом, контрастность аномалии ФКП в √m раз больше, чем контрастность отдельных методов.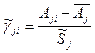
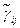 - сглаженные значения контрастности j -го метода в i -ой точке;
- сглаженные значения контрастности j -го метода в i -ой точке; 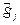 - стандарт сглаженных значений контрастности ФКП, который связан со стандартом несглаженных значений соотношением
- стандарт сглаженных значений контрастности ФКП, который связан со стандартом несглаженных значений соотношением 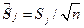 .
.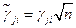 . Для ФКП
. Для ФКП 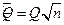 .
.
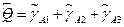 - результаты ФКП после предварительного сглаживания по трем точкам.
- результаты ФКП после предварительного сглаживания по трем точкам.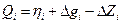 и построен график контрастностей ФКП для комплекса методов по профилю измерений. Экстремум контрастностей ФКП для выбранного комплекса методов можно считать надежной аномалией, если амплитуда ФКП превосходит величину тройного стандарта от фона комплекса методов. Подсчитаны фоновые значения ФКП и по правилу трех сигм выделена аномалия от рудной залежи для комплекса методов (рис.1.13.7)
и построен график контрастностей ФКП для комплекса методов по профилю измерений. Экстремум контрастностей ФКП для выбранного комплекса методов можно считать надежной аномалией, если амплитуда ФКП превосходит величину тройного стандарта от фона комплекса методов. Подсчитаны фоновые значения ФКП и по правилу трех сигм выделена аномалия от рудной залежи для комплекса методов (рис.1.13.7)