
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учет экономических показателей.Содержание книги
Поиск на нашем сайте
Для учета экономических показателей вводится понятие индекса стоимости
Рис. 2.9.3. Выбор оптимального значения индекса стоимости k по числу точек сети, попадающих в контур эллипса аномалии, и индекса стоимости Е по числу профилей, пересекающих эллипс аномалии: р – вероятность обнаружения объекта, с = в/а – коэффициент сжатия эллипсов аномалий.
Из рис.2.9.3 видно, что поиски с вероятностью обнаружения р < 0,65 не целесообразны, так как дальнейшее уменьшение вероятности не уменьшает стоимости работ k. В случае р > 0,65 индекс стоимости резко возрастает. По графику k можно определить оптимальное значение индекса стоимости k и вероятности обнаружения объекта не менее чем одной точкой р. Рассчитанная оптимальная сеть остается достаточно оптимальной в пределах 0,6< р <0,7. Это свойство называется инерционностью оптимальной сети. Для непрерывных наблюдений С. Х. Уорд предложил использовать график
Расчет сети наблюдений для слабых аномалий, соизмеримых с уровнем помех Для слабых аномалий расчет сети наблюдений ориентируется по энергетическому отношению аномалия-помеха
Величина энергии аномалии S
Рис. 2.9.4 Энергия аномалии
При расчете сети наблюдений для слабых аномалий, соизмеримых с уровнем помех, более важным становится не количество точек наблюдений, а различие в спектрах аномалии и помехи. При уменьшении шага съемки спектр помех обогащается высокочастотными составляющими и резко отличается от низкочастотного спектра аномалии от объекта, расположенного на глубине. Чем больше это различие, тем легче выделить аномалию от глубинного объекта. Различие в спектрах становится важнее, чем размеры аномалии по площади. Поэтому целесообразно уменьшать расстояние между точками наблюдений, т. е. увеличивать количество точек наблюдений m. Чем меньше шаг, тем легче установить наличие слабой аномалии, которая фиксируется рядом соседних точек низкочастотной составляющей аномалии от глубинного объекта поисков. Энергетическое отношение аномалия помеха Вероятность правильного обнаружения аномалии g определяется соотношением Интеграл вероятности определяется соотношением: Вероятность правильного обнаружения g определяется при условии равенства ошибок первого рода a (обнаружение ложной аномалии) и второго рода b (пропуск действительной аномалии). Правильный пропуск объекта определяется вероятностью j. На рис. 2.9.5 приведена зависимость вероятности правильного обнаружения аномалии g от энергетического отношения
Рис. 2.9.5. Зависимость вероятности правильного обнаружения аномалии g от энергетического отношения
Расчеты свидетельствуют, что когда r = 27 вероятность правильного обнаружения аномалии достигает 99,5 %. Таким образом, для такой надежности (достоверности) обнаружения аномалии необходимо, чтобы энергетическое отношение-аномалия помеха было бы более 27. Для заданного энергетического отношения r связь между средним квадратическим значением аномалии
Рис. 2.9.6. Связь между отношением сигнал-помеха
Зная При появлении коррелированной помехи увеличение энергетического отношения r достигается путем использования комплекса методов. Сгущение сети в этом случае не приводит к росту r, за счет увеличения количества точек m, поскольку вместе с m растет rx – интервал корреляции помехи: Поэтому увеличение r можно достичь только путем наблюдений на N профилях, где аномалия от объекта прослеживается, а помеха не коррелирует: Экономические показатели для слабых аномалий, соизмеримых с уровнем помех вводятся с учетом затрат на съемку, так как количество точек наблюдений может быть достаточно большим. Затраты на съемку площади S пропорциональны плотности съемки: Задача выбора оптимальной сети сводится к нахождению минимума функции потерь R, которая объединяет надежность обнаружения аномалии g и экономические показатели: На рис. 2.9.7 приведены расчетные значения функции потерь для слабых аномалий, соизмеримых с уровнем помех.
Рис. 2.9.7. Расчетные значения функции потерь для слабых аномалий, соизмеримых с уровнем помех.
Использование функции потерь имеет смысл лишь при малых отношениях аномалия помеха Третий подход к выбору сети наблюдений определяется не только оптимальным размером сети, но и формой сети, обеспечивающей максимальную вероятность подсечения объектов заданного вида. Например, для изометрических аномалий оптимальна шахматная сеть с точками наблюдений, расположенными в вершинах правильных треугольников.
При расчете сетей детализации сеть выбирается с расчетом фиксации всех деталий аномального поля. При съемке интерпретационных профилей, предназначенных для проведения количественных расчетов, расстояние между точками выбирается тем меньше, чем выше степень изменчивости геофизического поля. Шаг наблюдений выбирается из расчета Δ J = 0,5 % от J ср. Поэтому шаг часто неравномерен: более густой в эпицентре аномалии и менее густой на флангах. Кроме того, в любом случае фиксируются экстремумы аномалии, точки перегиба, точки перехода через нуль и другие особенности. На пятом этапе формирования рационального комплекса геофизических методов (рис. 2.3.1) рассматриваются вопросы обработки и интерпретации геофизических наблюдений для решения поставленной геологической задачи.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.97.170 (0.009 с.) |

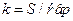 , где S/ав – среднее число точек сети, попадающих в контур эллипса аномалии, р – вероятность подсечения объекта. Индекс стоимости k равен стоимости обнаружения аномалии точками. Чем меньше k тем выгоднее сеть. Однако при этом снижается вероятность обнаружения объекта р. Связь индекса стоимости k и вероятности подсечения объектов не менее чем одной точкой р приведена на рис. 2.9.3. Оптимальное значение индекса стоимости выбирается на перегибе кривой k.
, где S/ав – среднее число точек сети, попадающих в контур эллипса аномалии, р – вероятность подсечения объекта. Индекс стоимости k равен стоимости обнаружения аномалии точками. Чем меньше k тем выгоднее сеть. Однако при этом снижается вероятность обнаружения объекта р. Связь индекса стоимости k и вероятности подсечения объектов не менее чем одной точкой р приведена на рис. 2.9.3. Оптимальное значение индекса стоимости выбирается на перегибе кривой k.

 по смыслу обратный индексу стоимости k. Оптимальной считается сеть, обеспечивающая максимум индекса Е. Из рисунка 2.9.3 видно, что для коэффициента сжатия эллипса аномалии с = 0,8 вероятность обнаружения р = 0,9 для случая Δ y/a= 1,0. Изменение Δ y/a в пределах от 0,8 до 1,15 уменьшает Е не более чем на 5 %. Рассчитанная оптимальная сеть продолжает оставаться оптимальной при значительных отклонениях реальных размеров объектов. Инерционность оптимальной сети сохраняется.
по смыслу обратный индексу стоимости k. Оптимальной считается сеть, обеспечивающая максимум индекса Е. Из рисунка 2.9.3 видно, что для коэффициента сжатия эллипса аномалии с = 0,8 вероятность обнаружения р = 0,9 для случая Δ y/a= 1,0. Изменение Δ y/a в пределах от 0,8 до 1,15 уменьшает Е не более чем на 5 %. Рассчитанная оптимальная сеть продолжает оставаться оптимальной при значительных отклонениях реальных размеров объектов. Инерционность оптимальной сети сохраняется. или
или  , где для некоррелированной помехи
, где для некоррелированной помехи  ,
,  - средний квадрат аномалии,
- средний квадрат аномалии,  - среднее квадратическое значение аномалии, m – число аномальных значений,
- среднее квадратическое значение аномалии, m – число аномальных значений, - амплитуда аномалии в i- ой точке.
- амплитуда аномалии в i- ой точке. рассчитывается путем решения прямой задачи с учетом точек, в которых амплитуда аномалии превышает 5-10 % от максимальной амплитуды
рассчитывается путем решения прямой задачи с учетом точек, в которых амплитуда аномалии превышает 5-10 % от максимальной амплитуды  (рис. 2.9.4).
(рис. 2.9.4).
 : m - количество точек наблюдений; аi - амплитуда аномалии в i -й точке.
: m - количество точек наблюдений; аi - амплитуда аномалии в i -й точке. , где Ф(t) – интеграл вероятности (рис. 1.7.10);
, где Ф(t) – интеграл вероятности (рис. 1.7.10);  .
.
 . На рис. 2.9.6 приведена связь между отношением сигнал-помеха
. На рис. 2.9.6 приведена связь между отношением сигнал-помеха  и количеством точек наблюдения m для заданной вероятности правильного обнаружения объекта g.
и количеством точек наблюдения m для заданной вероятности правильного обнаружения объекта g.
 .
. . Если помеха коррелирует по соседним профилям, то увеличение r достигается привлечением новых геофизических методов комплекса.
. Если помеха коррелирует по соседним профилям, то увеличение r достигается привлечением новых геофизических методов комплекса. , где
, где 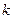 - коэффициент пропорциональности.
- коэффициент пропорциональности. , где
, где 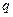 =(1-g) - вероятность безусловной ошибки обнаружения аномалии;
=(1-g) - вероятность безусловной ошибки обнаружения аномалии;  - ожидаемые прогнозные запасы полезного ископаемого в тоннах;
- ожидаемые прогнозные запасы полезного ископаемого в тоннах;  - разность между стоимостью одной тонны полезного ископаемого и себестоимостью ее добычи и переработки, чистая стоимость одной тонны потерь, т. е. удельные потери чистой прибыли на одну тонну сырья. Минимизация функции потерь R позволяет найти оптимальное число точек сети на единицу длины профиля
- разность между стоимостью одной тонны полезного ископаемого и себестоимостью ее добычи и переработки, чистая стоимость одной тонны потерь, т. е. удельные потери чистой прибыли на одну тонну сырья. Минимизация функции потерь R позволяет найти оптимальное число точек сети на единицу длины профиля 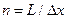 или площади
или площади  аномалии.
аномалии.



