
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статика плоской рыболовной сетиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Соотношения сил, растягивающих ячею сети. Чтобы определить основные силовые соотношения для плоской сети, предположим, что сеть ABCD (рис. 3.8) состоит всего из двух ячей. Сеть растянута внешними силами F1O и F2O, которые приложены к узлам и направлены вдоль диагоналей ячей. Они уравновешиваются натяжениями в нитях Т. Из условий равновесия узлов получаем F2O = 2Tcosa, F1O =2Tsina, откуда F2O = F1O ctga. (3.26) Теперь увеличим число ячей сети по каждой стороне в k раз, а шаг их пропорционально уменьшим в k раз. Тогда внешние усилия,, растягивающие ячею уменьшенных размеров вдоль ее диагоналей. F2 и F1 будут
F2 = F1 ctga.
Сравнивая выражения (3.27) и (3.26), видим, что соотношение сил F2 и F1 не зависит от размера ячеи. Положим, что шаг ячеи сети бесконечно мал, а число ячей бесконечно велико (непрерывная мoдель сети). Из-за малого шага ячеи можно считать, что по кромкам идеализированной сети внешние силы распределены равномерно. Тогда в пределах одной ячеи с достаточно. малыми диагоналями Dx: и D у напряжения будут
Их соотношение поэтому выразится как
а с учетом соотношения (3.27) получим s2 = s1ctg2a или
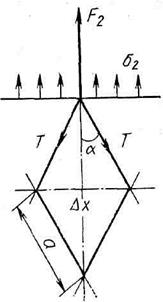
Для определения величины натяжения нитей рассмотрим схему, изображенную на рис. 3.12. Очевидно, что F2 = s2Dx= s 2 a sina. Кроме того, F2 = 2Tcosa. Приравнивая правые части, получим T = s2 a tga. (3.30)
Рассмотрение аналогичной схемы для горизонтальных сил Ft дает T = s1 a ctga.. (3.31) Таким образом, мы перешли к натяжению в отдельных нитях как функции от распределенной по сети внешней нагрузки, величины шага ячеи и посадки, т. е. перешли от непрерывной модели сети к дискретной. Соотношение сил, растягивающих сеть. Если сеть длиной L и высотой Н растягивается по кромкам вертикальными Py и горизонтальными Рx нагрузками, то, поскольку Рy = s2 L, Рx = s1 H, соотношение между ними будет
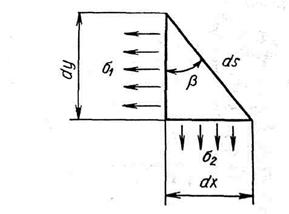
Взаимозависимость вертикальных и горизонтальных нагрузок учитывают при выборе коэффициентов посадки. Так, например, при иX = 0,5 в соответствии с выражением (3.29) имеем sy = 3sx, a при иX = 0,87 вертикальная нагрузка снижается до s y = l/3 sx. Отчетом этого иногда применяют посадку жаберных сетей и кошельковых неводов с большим иX. Для тралов же большие их нежелательны, поскольку это вызывает повышение стягивающих усилий по периметру трала и снижение его раскрытия. В сети, нагруженной вертикальными силами, возникает деформация ее боковых участков. Из рис. 3.13 видно, что левее линии ABC нагружены все четыре нити, выходящие из каждого узла. На участках, ограничиваемых линиями ABD и СВЕ, нагружены лишь три нити каждого узла, а в узлах, расположенных на участке, ограничиваемом линией DBE, нагружены только две нити в каждом узле. Вследствие этого узлы сети, расположенные правее линии ABC, стремятся сдвинуться влево. Аналогичное явление имеет место на левом боковом участке сети. Если же приложить к сети не вертикальные, а горизонтальные нагрузки, то выгибаться будут ее верхняя и нижняя кромки. По этой же причине (несимметричные нагрузки в узлах) расходятся края отверстия внутри сети при ее порывах. Сеть под действием параллельных сил, понятие о силовом поле сети. Пусть на прямоугольную сеть, рассмотренную ранее, помимо растягивающих сил, действуют дополнительные внешние силы qy равномерно распределенные по ее площади (рис. 3.14). Положим» что форма всех ячей сети сохраняется одинаковой, т. е. их = const, иy = const. Выделим из сети бесконечно малый элемент со сторонами dx и dy, нижняя кромка которого имеет ординату у, и рассмотрим условия его равновесия (рис. 3.15). С учетом размеров элемента внешняя сила, приходящаяся на его площадь, будет qdxdy.
Тогда, проектируя все силы на ось Y, получим (s2 + d s 2)dx – s 2dx – qdxdy = 0 или d s 2 – qdy = 0, откуда после интегрирования и определения произвольной постоянной s 2 = qy+ s 2О (3.33) С учетом выражения (3.28) получим s 1 = (qy+ s 2О)tg2a. 3.34) На любой горизонтальной линии у = const величины s1 и s2 неизменны. Но вдоль других линий сети, например вдоль линии MN (см. рис. 3.14), характеризуемой углом b, они изменяются. Такую идеализированную сеть можно рассматривать как силовое поле s1 или s 2. Линии уровня у = const совпадают здесь с горизонтальными диагональными линиями ячей сети, а градиент этого поля совпадает с вертикальными диагональными линиями. Градиенты поля с учетом выражений (3.33) и (3.34) будут
Изменение s 1 и s 2 вдоль любой линии MN найдем с учетом того, что линейный элемент ds вдоль линии MN будет ds == dy/cos b, поэтому градиенты s 2 и s 1 вдоль линии MN составят
Силовое поле сети может представлять собой поля нескольких сил, которые связаны между собой. Так, помимо рассмотренных сил s1 и s2 имеет место поле сил натяжения нитей N, внешних сил q и скалярное поле коэффициента посадки и(х, у) — факторов, которые в общем случае могут быть переменными по поверхности сети.
Обеспечение требуемой формы сети. Пусть задана требуемая форма сети ABCD, показанная на рис. 3.16. Чтобы эта форма была обеспечена, необходимо приложить по кромке сети ВС соответствующие силы (sx)S и (sy)S. Для их определения выделим малый участок сети, представляющий собой прямоугольный треугольник, гипотенуза которого совпадает с косой кромкой сети ВС (рис. 3.17). Очевидно, что sy dx= (sy)Sds, откуда аналогично sy dx= (sy)Sds
Таким образом, приложение сил (sх)S и (sy)S по кромке ВС наряду с приложением сил sx по кромке AD и sy по кромкам АВ и АС обеспечивает требуемую форму АВСД нагруженной сети. Статика плоской рыболовной сети. Если к горизонтальным кромкам плоской прямоугольной сети приложены вертикальные растягивающие нагрузки РВ (рис. 16), то для того чтобы сеть сохранила форму прямоугольника, к ее вертикальным кромкам должны быть приложены соответствующие по величине горизонтальные растягивающие усилия Рг. Связь между вертикальными и горизонтальными усилиями имеет вид
Растягивающая нагрузка, приходящаяся на единицу длины кромки сети, называется напряжением и обозначается s1=РГ/h= s1= РB/1. (3.42) Напряжения связаны между собой выражением
Под действием нагрузок, приложенных к кромкам сети, в ее нитях возникают натяжения Г, вычисляемые по формулам: T=sy·a·tga, (3.43) T = sx·a·ctga. (3.44) Если помимо нагрузок по горизонтальным и вертикальным кромкам сети в ее плоскости действуют равномерно распределенные силы q (сила тяжести или гидродинамического сопротивления), то напряжения в каждой точке сети определяются по формулам: s2=qy+s20 (3.45) s1=(qy+s20)tg2 a. (3.46) Такая сеть находится всиловом поле s2 и s1. Линии уровня у = const совпадают в рассматриваемом случае с горизонтальными диагоналями ячей, а градиент поля — с вертикальными диагоналями (х= const).
В качестве примера изломов в сети рассмотрим рис. 3.18. Посаженная на подборы сеть ABCD первоначально имела прямоугольную форму с равным количеством ячей по всем сторонам. После закрепления сети к обручу точки ABCD лежат на окружности с центром О. Коэффициенты посадки по кромкам сети стали соответственно uAB =sina1 uDC =sina3 uAD = uBC =cos(a1+a3)/2 (3.47)
Последнее равенство вытекает из того, что 2(a1 + 2a2 + a3) = 360° или a 2 = 90 - ( a 1 + a3)/2. Из рис. 3.18 видно, что поле такой сети составлено как бы из четырех отдельных регулярных силовых полей. Их границы — линии излома, на которые ложится дополнительная нагрузка, следствием чего именно вдоль них прежде всего может иметь место обрыв нитей. Рассмотрим еще один пример. Пусть из прямоугольной сети ABCD вырезали кусок FEG и затем сеть соединили по кромкам EF и GF. Кромка ЕМ является линией излома, и вдоль нее возникает дополнительная нагрузка Т. Однако структура этой кромки такова, что она этой нагрузки воспринимать не может. Вот почему для подкрепления подобных кромок необходимо ставить топенанты и пожилины.
Литература: [1], стр. 75-92. Вопросы для самоконтроля 1. Какую форму принимает сетное полотно, посаженое с разными коэффициентами по верхней и нижней подборе? 2. Какова зависимость между горизонтальным и вертикальным посадочными коэффициентами? 3. Как определяется натяжение в сети при её линейной деформации?
Сетные оболочки
Рассмотрим некоторую поверхность вращения (рис. 3.21), да которую нужно наложить сеть. Для однозначного определения требуемой формы сети необходимо зафиксировать посадку ее вдоль параллели П0 и меридиана М, т. е. задать и0 и им = f(s), где s — длина меридиана. Задание требуемой посадки иM вдоль меридиана можно осуществить, пропустив вдоль него канатную подбору. Такая сеть будет иметь правильную структуру (без изломов), если диагональные линии ятей будут направлены соответственно по меридианам и параллелям оболочки (т. е. диагональные линии являются линиями кривизны поверхности).
Упрощенная расчетная схема. При обосновании упрощенных методов расчета сетей введены следующие допущения: сеть имеет вид поверхности вращения, диагональные линии ячей совпадают с параллелями и меридианами поверхности, неравномерность размера ячей отсутствует, размер ячей весьма мал по сравнению с размерами сети, сетные нити нерастяжимы.
Линии уровня поля s = const совпадают с параллелями, а изменение
На поверхности сети выделим двумя меридианами узкую Полоску шириной dy, а на ней — участок длиной ds. Действующие на выделенный элемент ABCD внешние гидродинамические силы Р уравновешиваются внутренними усилиями по его кромкам sx и sy (рис. 3.23). Суммарное внутреннее усилие по кромке AD есть Тм= sxr d j, (3.48) где r — радиус параллели кромки.
Суммарное внутреннее усилие покромке АВ будет Tn= s yds. (3.49) Внутренние силы ТП, действующие по параллелям, вызывают некоторое сжимающее усилие ТZ, направленное по оси Z. На рис. 3.24 видно, что составляющие ТY взаимно уравновешиваются, а сумма составляющих Tz дает силу Tz = 2TПsin(dj/2) или, учитывая, что величина dj мала, Tz = 2TПdj а с учетом выражения (3.43) Внешняя гидродинамическая сила Р, действующая на выделенный элемент сети, может быть представлена как P = pdF Или P = pr dj ds. (3.51) Если представить ее состоящей из двух компонент: рx — по оси X и py — по радиусу r, то Px = pxr dj ds, (3.52) Рy = pyr dj ds. Полоску сети шириной rdy можно заменить гибкой нитью — плоским эквивалентом пространственной сети и ее силового поля, который представляет собой меридиональное сечение поверхности сети. Для этого умножим все силы на коэффициент k = 1/ dj и с учетом этого определим силы, действующие на единицу длины гибкой нити. Натяжение нити по выражению (3.48) будет
Сжимающее усилие по выражению (3.50) будет
Это усилие, являющееся для нити внешним, для сети будет внутренним и на нее не действует. Составляющие внешней гидродинамической силы, приложенной к элементу нити, с учетом выражения (3.52) будут
Схема приложения этих сил показана на рис. 3.25. Рассматриваемая гибкая нить — плоский эквивалент сети — имеет особое свойство: ее длина, как и величина действующих на нее внешних| сил, зависит от формы ячеи в сетной оболочке. Так, например, выражение (3.54) можно представить как qC = sy=sxtg2a или с учетом выражения (3.53)
Уравнения равновесия. Уравнения равновесия гибкой нити — плоского эквивалента сетной оболочки — в проекциях на натуральные оси t и n будут
где Fx и Fy — проекции внешних сил соответственно на направления касательной и нормали; Ry — радиус кривизны гибкой нити. Натяжение T определяется по формуле (3.53). Проекции внешних сил имеют вид Fx = qx cos g + (qC — qy) sin g, (3.60) Fy = qx sin g + (qC — qy) cos g,
где g — угол, определяющий направление оси t относительно оси X или соответственно оси п относительно оси Y. Различные решения уравнений (3.59) будут зависеть от конкретного вида функций F1 и F2, которые сложным образом зависят от формы сети, формы и размеров ячеи и от ряда задаваемых дополнительных условий или требований к форме сети, ее раскрою, посадке и натяжениям в нитях. Дополнительные условия вводятся в дифференциальные уравнения. Их решения получают, как правило, с помощью ЭВМ. Задачи расчета оболочки произвольной формы являются еще болеесложными и достаточных решений пока не имеют. Определение формы сети графоаналитическим методом. Для случая, когда сеть имеет форму тела вращения, вид кривой ее меридиального сечения можно получить графоаналитическим методом. На рис. 3.26 кривая АО'В — меридианное сечение сетной поверхности плоскостью, проходящей через ось вращения X. Внутреннее давление отсутствует. Сеть посажена на два обруча. Один из них закреплен, а второй нагружен осевой силой. Пусть в некоторой точке С' поверхности главные радиусы кривизны будут r1 и r 2. Соотношение их можно определить при помощи одного
из основных уравнений равновесия сетной оболочки произвольной формы:
При отсутствии внутреннего давления Q = 0 и
Искомую кривую А В получим как сопряжение большого числа малых дуг, проводимых соответствующими радиусами r1. Точность построения тем выше, чем меньшей длины будут эти дуги. Величина r1 определится из выражения (3.62):
а с учетом выражения (3.29) получим
Для начала построения необходимо знать величину желаемого радиуса окружности г2 и коэффициента посадки и2 в наиболее узком месте тела вращения. Если ось X совместить с осью вращения, а начало координат поместить так, чтобы ось Y проходила через сеть в наиболее узком месте, то величина r2 будет равна радиусу окружности в этом сечении (r2 = у), причем оба радиуса кривизны r1 и r 2 лежат на оси ординат. Значение и2 легко определить из равенства sy и2 = 2паи2 = 2tу (3.65) где sy — ширина сетного полотна в жгуте; п — число ячей по ширине; а — шаг ячеи. Отсюда
Построение ведем следующим образом. На оси ординат (рис. 3.27) отмечаем точку A, где r 2 = у — желаемому радиусу наиболее суженной части сети. Затем по формуле (3.57) определяем r1 и, откладывая его на оси Y, находим центр кривизны В. Отсюда радиусом r1 описываем малую дугу АА’. Если теперь провести из точки B через точку А’ прямую до пересечения с осью X, то новое значение r2' будет равно A’O’, а новое значение у1 будет А'А1’. Подставляя его в выражение (3.66), находим значение и '2, а затем с помощью выражения (3.64) находим значение r’1 для следующей малой дуги искомой кривой. Откладывая от точки А' отрезок r’1, найдем точку В' — новый центр кривизны. Из точки В' радиусом r’1 описываем следующую малую дугу А’ А” и т. д., постепенно строим один квадрант меридионального сечения сети.
Расстояние между обручами L = 2х/r0 определяют по графику из соотношений L/r = 2AB/AC, L = 2r·0,55/0,76 =1,5r, где r — радиус обруча. Наклонные прямые на графике соответствуют различным соотношениям r/(L/2) = D/L.
Практически часто нужно знать требуемые размеры сетного полотна в жгуте sx и sy для постройки сети (например, секция вентеря) требуемой формы. Зависимости между размерами сетей в жгуте и размерами их после прикрепления к обручам приведены в работе Н. Н. Андреева «Проектирование кошельковых неводов». Раздел 4. Механика основных орудий лова
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.016 с.) |



 и
и 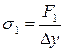

 (3.29)
(3.29)
 (3.32)
(3.32)


 (3.35)
(3.35)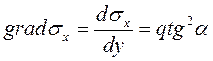 (3.36)
(3.36)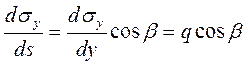 (3.37)
(3.37)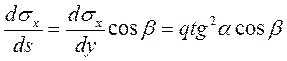 (3.38)
(3.38)
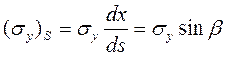 (3.39)
(3.39) (3.40)
(3.40) (3.41)
(3.41) (3.42.а)
(3.42.а)
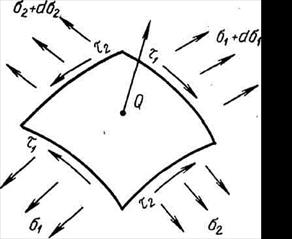 Особенности расчета сетных оболочек. Общие уравнения равновесия рыболовной сети произвольной формы составлены А. И. Зоновым. Для этого рассматривается элементарный криволинейный четырехугольник (рис. 3.19), стороны которого совпадают с диагональными, линиями ячей сети, нагруженной некоторой внешней силой Q. На кромках сети, помимо нормальных напряжений s, возникают в общем случае и касательные напряжения t. Расчет сетной оболочки осуществляется путем решения системы дифференциальных уравнений равновесиями использования некоторых геометрических соотношений. Ограничим рассмотрение существующих методов расчета только некоторыми вопросами, относящимися к сетям типа сетной оболочки вращения. При определенных допущениях к таким оболочкам можно отнести сети тралов, кошельковых неводов и других орудий лова. Так, например, в качестве исходной для трала можно рассматривать сетную оболочку, посаженную на круглый обруч П0 (рис. 3.20). Рассчитав исходную оболочку, т. е. определив ее размеры, раскрой, ассортимент делей и нагрузки в нитях, затем отрезаем излишние сети по назначенным линиям подбор П1 и П2. Действие отброшенных сетей заменяем соответствующими усилиями оснастки, приложенными к подборам П1 и П2.
Особенности расчета сетных оболочек. Общие уравнения равновесия рыболовной сети произвольной формы составлены А. И. Зоновым. Для этого рассматривается элементарный криволинейный четырехугольник (рис. 3.19), стороны которого совпадают с диагональными, линиями ячей сети, нагруженной некоторой внешней силой Q. На кромках сети, помимо нормальных напряжений s, возникают в общем случае и касательные напряжения t. Расчет сетной оболочки осуществляется путем решения системы дифференциальных уравнений равновесиями использования некоторых геометрических соотношений. Ограничим рассмотрение существующих методов расчета только некоторыми вопросами, относящимися к сетям типа сетной оболочки вращения. При определенных допущениях к таким оболочкам можно отнести сети тралов, кошельковых неводов и других орудий лова. Так, например, в качестве исходной для трала можно рассматривать сетную оболочку, посаженную на круглый обруч П0 (рис. 3.20). Рассчитав исходную оболочку, т. е. определив ее размеры, раскрой, ассортимент делей и нагрузки в нитях, затем отрезаем излишние сети по назначенным линиям подбор П1 и П2. Действие отброшенных сетей заменяем соответствующими усилиями оснастки, приложенными к подборам П1 и П2.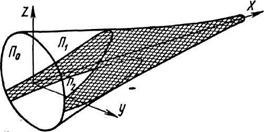


 градиента поля происходит вдоль меридианов.
градиента поля происходит вдоль меридианов.

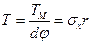 (3.53)
(3.53) (3.54)
(3.54)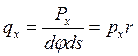 (3.55)
(3.55) 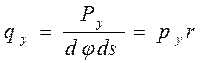 (3.56)
(3.56)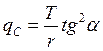 (3.57)
(3.57)

 , (3.59)
, (3.59)
 (3.61)
(3.61) (3.62)
(3.62) , (3.63)
, (3.63) (3.64)
(3.64) (3.66)
(3.66)



