
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопротивление деталей орудий лова, имеющих форму пластины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Форму пластины имеют, например, такие детали оснастки орудий лова, как траловые распорные доски и подъемные щитки.
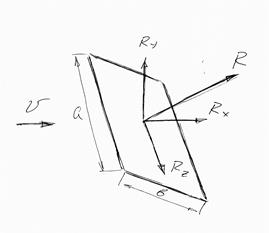
Рис. 1.6. Проекции вектора равнодействующей сопротивления пластины на координатные оси.
Для пластины, расположенной под некоторым углом a к направлению движения, результирующая гидродинамических сил R может быть разложена на составляющие: силу лобового сопротивления Rx, подъемную (или распорную) силу Ry, боковую силу Rz. Точка приложения равнодействующей сил сопротивления (центр давления) при изменении угла а лежит на продольной оси симметрии пластин между передним ее ребром и поперечной осью симметрии. Значения составляющих рассчитываются по формулам: где сх, су, cz — гидродинамические коэффициенты этих сил.
Отношение cу/сх, т.е. коэффициентов подъемной силы и лобового сопротивления, называется гидродинамическим качеством. Гидродинамическое качество k пластины определяется из отношений: k=Cylcx=Ry/RX: (1.28) Его величина имеет максимальное значение при малых углах атаки. В качестве примера на рис. 17 показана зависимость гидродинамического качества пластины от угла атаки при X = 0,5.
Значения коэффициентов сх и сх для некоторых прямоугольных пластин в зависимости от угла а и удлинения X приведены на рис. 1.7 и 1.8.
В общем случае для пластины любой формы удлинением называют отношение
где а размах; F — площадь пластины
Значения коэффициента лобового сопротивления сх для квадратной или круглой пластины, плоскость которой расположена перпендикулярно направлению движения, в зависимости от числа Рейнольдса показаны в приложении 6. Удлинение пластины находится из выражения l=a2/F. (1.30) Для прямоугольной пластины l =а/b, (1.31) где а – размах пластины; b – ее хорда. Коэффициент центра давления Cd1 находится из отношения Cd1=х1d/b, (1.32) где х1d — расстояние между передним ребром пластины и центром давления. Вектор результирующей гидродинамических сил R в общем случае не проходит через начало координат и создает моменты относительно осей X,Y,Z. Момент Mz (относительно оси Z) находится из выражения
где тг — коэффициент гидродинамического момента. Зависимости указанных гидродинамических коэффициентов от угла атаки для профилированных пластин индивидуальны для каждого профиля пластины и ее формы в плане. Связь между значениями гидродинамических коэффициентов определяется выражением
Сопротивление пластины, параллельной течению, целиком обусловлено силами трения и находится по формуле
где Cf — гидродинамический коэффициент трения
Коэффициент трения Сf зависит от числа Рейнольдса. Для условия Re<104 Для условий 106<Re<2*107 c f =0,074/Re1/5 (1.37) В диапазоне. 104 <Re<106 коэффициент cf принимает промежуточные значения. В соотношениях (1.36) и (1.37) число Re находится как
Для расчета сил трения также используются формулы: для условия Re<104 R= 0,7b -0,57Fv 1,5 (1.39) и для условия 106<Re<2*107 R=2,3b-0,2Fv 1,8 (1.40) Расчет подъемной силы Ry и силы лобового сопротивления Rx гидродинамических щитков, применяемых для оснастки тралов, аналогичен изложенным выше расчетам для пластины. Для оснастки орудий лова применяются также тела и более сложных форм, чем рассмотренные выше (стяжные кольца кошелькового невода, поплавки и грузила в виде цилиндров с закругленными или конусообразными концами и т. д.). Сопротивление деталей орудий лова, имеющих форму цилиндра. Форму цилиндра имеют поплавки и грузила, применяемые для оснастки подбор кошельковых неводов, закидных неводов, плавных и ставных сетей. Близки к цилиндрической форме прямолинейные тросы, канаты и нитки. Гидродинамические коэффициенты для цилиндра зависят от формы его сечения (круг, эллипс...), Re, удлинения l (отношения длины l к диаметру d), угла атаки a. Для кругового цилиндра значения гидродинамических коэффициентов находятся в три этапа. Сначала находится значение коэффициента Cб.у для цилиндра бесконечного удлинения (l>40) при расположении оси цилиндра перпендикулярно вектору скорости набегающего потока в зависимости от числа Рейнольдса. Зависимость Cб.y=f(Re) для цилиндра с круговым сечением показана в приложении 4. Re определяется из соотношения (1.24). Далее уточняется значение гидродинамического коэффициента с учетом его фактического удлинения: Ск.У=Сб.уk(λ). (1.41) Данные о поправочном коэффициенте k(l) приведены в приложении» 5. Затем находятся гидродинамические коэффициенты подъемной силы су и лобового сопротивления сх в зависимости от угла атаки a: CY = CКY.sin2acosa; (1.42) CХ = CKYsin2a. (1.43) Ориентировочные значения коэффициентов сопротивления для цилиндров бесконечного удлинения при расположении оси перпендикулярно вектору скорости набегающего потока: для эллиптического сечения Сб.у=0,2; для цилиндра, имеющего в сечении форму тела наилучшего обтекания, Сб.у=0,026. Качественно сопротивление прямолинейных тросов, канатов и ниток подчинено тем же закономерностям, что и сопротивление гладких цилиндров. Количественно значения гидродинамических коэффициентов этих тел отличаются существенно. Поэтому значения коэффициентов для цилиндра могут использоваться лишь в ориентировочных расчетах гидродинамических сил, действующих на прямолинейные тросы, канаты и нитки. Гидродинамические коэффициенты для прямолинейных стальных тросов, расположенных под углом а к потоку, могут быть найдены по формулам:
cУ= a sin2acosa; (1.45) cZ = ±bsin3acosa, (1.46) где C90 — коэффициент сопротивления троса, ось которого расположена перпендикулярно направлению движения, его значение может быть принято равным 0,9—1,15; CO — коэффициент сопротивления троса, ось которого совпадает с направлением движения, его значение находится в пределах 0,02—0,03; а - эмпирический коэффициент, равный 0,92; b - эмпирический коэффициент, значение которого зависит от диаметра троса следующим образом:, для тросов диаметром 18—20 мм b = 0,65; для тросов диаметром 20—25 мм b = 0,65-1,0; для тросов диаметром больше 25 мм b = 1,0. Формула (1.46) справедлива для стальных шестипрядных тросов. Знак «минус» здесь относится к тросам правой свивки, знак «плюс» — к тросам левой свивки. Таким образом, направления боковой силы Rz для тросов правой и левой свивок противоположны. Характерную площадь F в этом случае следует вычислять как произведение хорды и диаметра каната.
|
|||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.008 с.) |

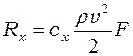 (1.25)
(1.25) (1.26)
(1.26)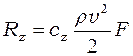 (1.27)
(1.27)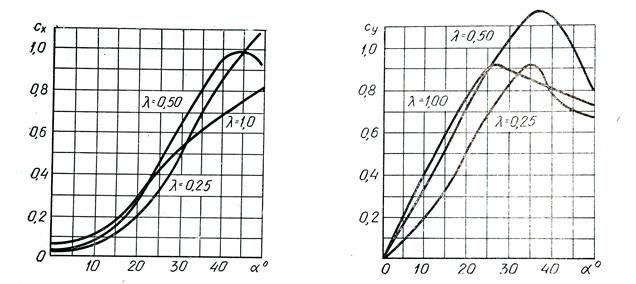
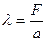 (1.29)
(1.29) (1.33)
(1.33)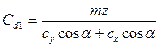 (1.34)
(1.34)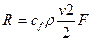 (1.35)
(1.35)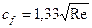 (1.36)
(1.36)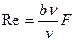 (1.38)
(1.38)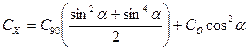 (1.44)
(1.44)


