
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы веса и трения; усилия, развиваемые рыбой
Силы веса, действующие на орудия лова, распределены по площади сетей, по длине канатов или сосредоточены в местах крепления соответствующих элементов оснастки данного рыболовного орудия. Результирующая сила тяжести Р орудия лова (или какой-либо его детали) при всех положениях орудия лова направлена по вертикали вниз. Результирующая гидростатических (архимедовых) сил D направлена вертикально вверх. Значения Р и D определяются по формулам: P=gV=r*g*V, D=gBV==r*gB*V (1.1) где V — объем тела, м3; g — объемный вес тела, Н/м3; gB — объемный вес воды, Н/м3. Силы P и D действуют в противоположных направлениях. Их равнодействующая Q, когда силы PhD лежат на одной вертикали, выражается как Q = P — D (1.2) и является весом тела в воде. Если Р и D не лежат на одной вертикали, появляется, кроме того, момент М, изменяющий положение погруженного тела, пока М не станет равным нулю или не уравновесится реакцией соответствующих связей Вес тела в воде с учетом выражений (1.1) представляется в виде
где r — плотность материала детали, кг/м3; rв — плотность воды, кг/м3. Положительными будем считать силы веса в воде Q, направленные вертикально вниз, что имеет место при r > r В. Если же r < r В, то величина Q получается отрицательной и представляет собой силу плавучести. Абсолютная величина множителя (r — r В)/ r показывает, во сколько раз вес тела в воде или его плавучесть Q отличается от веса тела в воздухе Р. При определении веса в воде сетеснастных материалов учитывается их особая, как бы пористая, структура, вследствие чего истинный объем материалов изделия значительно меньше, чем внешний объем изделия. Таким образом, в выражениях (1.1) для сетеснастных изделий следует различать истинный объем Vист и внешний объем VBH. Сила тяжести таких изделий (ниток, веревок, канатов, сетей) может быть определена выражениями Р = g Vист; Р = g ФVВН, (1.4) где g Ф — фиктивный объемный вес изделия, Н/м3. Соответственно сила плавучести D для сетеснастных материалов будет D=yB Vист. (1.6) Объемный вес материала ниток, канатов и сетей после предварительного экспериментального определения сил P и D вычисляется по формуле
Объемный вес сетематериалов и их плотность r связаны: g=rg, (1.8) где g — ускорение силы тяжести, м/с2. Таблица 1.1 Величины g для некоторых веществ, материалов и сред.
Средний объемный вес в воде g * ниток и канатов определяется из
Силы трения. Силы трения сетей, канатов и деталей оснастки по грунту существенным образом влияют, а иногда и определяют работу многих орудий промышленного рыболовства (например, донных тралов, донных и закидных неводов, донных плавных сетей). В случае использования стационарных орудий благодаря силам трения осуществляют установку орудия и получают необходимую его форму. Это обеспечивается применением различного рода грузил, балластов, якорей, которые противодействуют течению и волнению, препятствуя деформированию и сносу орудия лова. Сила трения при движении деталей оснастки по грунту, например, грунтропа (рис1.1) определяется выражением F=Nf=Gf (1.11)
где N —реакция грунта; G — вес грузила в воде; f — коэффициент трения. Держащая сила балласта на канатной оттяжке рассчитывается по формуле
Отсюда, естественно, следует, что держащая сила балласта увеличивается с увеличением его веса и коэффициента трения и уменьшается при увеличении угла а оттяжки с горизонталью. При а = 90° держащая сила балласта становится равной нулю. Держащая сила якорей зависит от их конструкции и определяется по эмпирическому выражению F=kG (1.13) где G — вес якоря; k — опытный коэффициент. Величина k зависит от типа якоря и характера грунта. Для адмиралтейских якорей k ≈ 8 (на песчаном грунте) и k≈ 15 (на глинистом грунте). В случае движения орудий лова непосредственно по дну (плавные сети, донные невода, тралы и т. п.) сопротивление грунта направлено против скорости. В этом случае сопротивление грунта лишь условно можно рассматривать как сопротивление трения, ибо его природа значительно сложнее. В действительности орудия лова и их детали при движении по грунту, находящемуся в состоянии полного насыщения водой, частично сдвигают и гребут перед собой верхний его слой. Тем не менее ввиду сложности явления в первом приближении сопротивление орудий лова при движении по дну рассматривается как трение скольжения и для определения силы трения используется соотношение (2-9).
Значения коэффициента трения для некоторых пар тел в воде приведены в табл. 1.2. Таблица 1.2
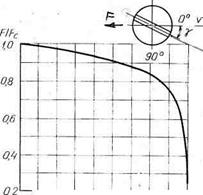
Особенно существенно влияние сил трения о дно при работе донными неводами, где силы трения являются основным видом внешних нагрузок. Они определяют форму урезов и в итоге уловистость орудия лова. В результате опытов В. А. Ионаса по изучению процесса трения канатов в воде по песчаному грунту было выяснено, что коэффициент трения комбинированных и стальных рыболовных канатов зависит от направления движения, материала и толщины каната, что обусловлено главным образом некоторым зарезанием каната в грунт (Рис 1.2). При движении каната вдоль оси (угол b = 0) коэффициент трения для всех образцов практически одинаков и в среднем равен 0,7 + 0,1. Коэффициент трения растительных канатов от направления движения практически не зависит и также равен в среднем 0,7 ±0,1. Экспериментальную оценку сил трения металлических траловых бобинцев осуществил Г. Е. Биденко путем протаскивания последних в грунтовом канале. При угле тяги g = 0° (рис. 1.3) имеет место чистое скольжение бобинца, а при у = 90° — чистое качение его. Наибольшая величина сопротивления наблюдается, когда ось бобинца совпадает с направлением тяги, т. Е. при g = 0°. Для этого случая силу трения скольжения можно определить как FC = 0,6G, (1.14) где G — вес бобинца в воде. Величину суммарной силы трения F (от скольжения и качения) в зависимости от угла у можно определить из графика, изображенного на рис. 1.3. Из него видно, что почти во всем диапазоне углов тяги трение скольжения является преобладающим.
Усилия, развиваемые рыбой. Статическое усилие R0, развиваемое рыбой, рассчитывается по формуле Ro=kОPL-1/3. (1.15) Коэффициент kО получается опытным путём Максимальное динамическое усилие R, развиваемой рыбой определяется кинетической энергией рыбы и вызванным этой энергией упругим перемещением снасти. Сила, приложенная к снасти: R=cx, где с – жёсткость снасти, Н/м, – упругое перемещение, м.
Работа, произведённая рыбой по перемещению при увеличении нагрузки от 0 до R:
А кинетическая энергия рыбы при броске
откуда находится из выражения
Необходимая величина упругого перемещения снасти для условия, при котором динамическое усилие, развиваемое рыбой, не должно превышать собственного ее веса, определяется соотношением
Вес рыбы в воде РВ связан с весом ее в воздухе. Р соотношением РВ= (0,01-0,02) Р. (1.18) Вертикальная потопляющая сила РП, создаваемая попавшей в орудие лова рыбой, приближенно оценивается выражением PП = 0,07Р, (1.19) где РП — потопляющая сила, создаваемая уловом.
Литература: [1], стр. 50-59
Вопросы для самоконтроля
1. Как определить вес объекта в воде? 2. Как рассчитываются силы воздействия рыбы на орудие лова? 3. Что такое держащая сила якорей? 4. Как определить держащую силу балласта и грузил?
ГИДРОДИНАМИЧЕСКИЕ СИЛЫ Сопротивление среды при движении орудий лова Изучение гидродинамических сил, действующих на рыболовные орудия, движущиеся в воде или установленные на течении, базируется на общих принципах гидродинамики. Первой проблемой в
Известно, что величина гидродинамического сопротивления данного тела зависит от двух факторов: интенсивности вихре- и волнообразования вокруг тела и свойств самой жидкости. В соответствии с теорией Гельмгольца—Кирхгофа струйки жидкости, приближаясь к препятствию, например к пластине, отклоняются от первоначального направления и плавно обтекают переднюю сторону пластины (рис. 1.4). За пластиной струйки срываются с ее кромок и текут дальше, отделяя застойную область, где скорость жидкости равна нулю. Давление за пластиной соответствует гидростатическому, а перед ней — повышенное. В опытах распределение давления оказывается близким к теоретическому в передней части тела и значительно отличается в задней части, где образуются вихри и давление падает. Разница истинных давлений дает так называемую силу сопротивления формы тела. Кроме того, в вязкой жидкости существует трение между ее частицами и поверхностью тела, которое также направлено против движения. Сумму этих двух сил — сопротивление формы и сопротивление трения — называют сопротивлением тела.
В прикладной гидромеханике для определения величины гидродинамического сопротивления движущегося тела пользуются выражением Ньютона R = k r Fv2, (1.20) где k — безразмерный опытный коэффициент, зависящий от формы тела и физических условий движения; r — плотность жидкости, кг/м3; F — характерная площадь тела, м2; v — скорость движения жидкости относительно тела, м/с; R — гидродинамическая сила, Н. В общем виде величину коэффициента гидродинамического сопротивления k можно представить как k = Ф(r, l, v, m, a, g, a0), (1.21) где r —плотность жидкости, кг/м3; l —характерный линейный размер тела, м; v — характерная скорость движения тела в жидкости, м/с; m— коэффициент вязкости жидкости, Н·с/м2; a — коэффициент поверхностного натяжения, кг/с2; g — ускорение силы тяжести, м/с2; а0 — скорость звука в жидкости, м/с. На величину коэффициента сопротивления движению тела в жидкости наибольшее влияние имеют вязкость жидкости, размеры тела, скорость движения и соответственно обобщающее их число Рейнольдса
где v — коэффициент кинематической вязкости, м2/с.
Формула сопротивления тела (1.20) часто используется в виде
где с — безразмерный гидродинамический коэффициент; р — плотность жидкости, кг/м3; v — скорость движения тела (жидкости), м/с; F — характерная площадь тела, м2. Безразмерный коэффициент c рассчитывают по данным опытов. В таких опытах, выполняемых обычно в гидроканалах или аэродинамических трубах, непосредственно измеряется сила сопротивления R, действующая на тело при скорости v, плотность жидкости (или газа) р и характерная площадь тела F. Подсчитанные из опытов значения с относятся к соответствующим каждому эксперименту значениям числа Рейнольдса, и результаты опытов представляются для практического пользования в виде функций с = f(Re). Нетрудно видеть, что безразмерные коэффициенты сопротивления k из выражения (1.20) и с из выражения (1.23) имеют одинаковый физический смысл и связаны постоянным числом множителем, а именно с = 2k. При скоростях движения v, меньших скорости звука а0, сжимаемоcть газов не проявляется и законы их течения вокруг тел те же, что и для жидкостей. Поэтому при v < а О выражение (1.23) пригодно для расчета сопротивления тел, движущихся в воде, воздухе и других жидких и газообразных средах. Значения r и v для воды и воздуха, т. е. для сред, в которых обычно проводятся эксперименты по определению сопротивления в гидроканалах и аэродинамических трубах приведены в табл. 1.3. Таблица 1.3
Сказанное выше вполне справедливо для деталей оснастки рыболовных орудий, имеющих стабильную форму и обтекаемых потоком жидкости. Что же касается сетей, то определение гидродинамических сил для них имеет ряд рассматриваемых ниже особенностей, вызванных проницаемостью сети и нестабильностью ее формы.
Детали оснастки орудий лова представляют собой тела, близкие по форме, к шарам, цилиндрам и пластинкам (плоским и профилированным).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.12.222 (0.032 с.) |
 или
или  (1.3)
(1.3) (1.7)
(1.7) (1.9)
(1.9) (1.10)
(1.10)
 (1.12)
(1.12)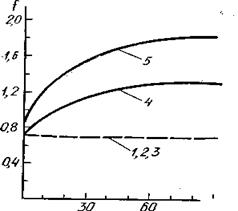
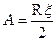 ,
,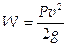 ,
,
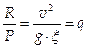 (1.16)
(1.16)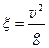 (1.17)
(1.17) этом плане, возникшей в начале XX века, является проблема определения суммарного сопротивления среды. Значительно позже возникли задачи о распределении гидродинамических сил по сетной поверхности рыболовного орудия. Хотя форму рыболовных орудий определяют исходя из поведения рыбы в процессе лова, однако представляет также интерес выбор внешних форм орудия лова и с гидродинамической точки зрения. При этом имеется в виду обеспечение наименьшего сопротивления, установление наиболее выгодного гидродинамического влияния деталей орудий лова на уловистость, обеспечение минимума деформации рыболовных орудий.
этом плане, возникшей в начале XX века, является проблема определения суммарного сопротивления среды. Значительно позже возникли задачи о распределении гидродинамических сил по сетной поверхности рыболовного орудия. Хотя форму рыболовных орудий определяют исходя из поведения рыбы в процессе лова, однако представляет также интерес выбор внешних форм орудия лова и с гидродинамической точки зрения. При этом имеется в виду обеспечение наименьшего сопротивления, установление наиболее выгодного гидродинамического влияния деталей орудий лова на уловистость, обеспечение минимума деформации рыболовных орудий. (1.22)
(1.22) (1.23)
(1.23)


